Министерство образования республики Беларусь
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ РАДИОФИЗИКИ И КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ
Кафедра физики и аэрокосмических технологий
Лабораторная работа № 2
Определение поверхностного натяжения жидкости методом отрыва кольца
Боброва Надежда Михайловна
студентка 2 курса 55 группы
биологического факультета
специальность
«биотехнология»
Преподаватель:
кандидат физико-математических наук,
доцент Прокопович И.П.
Минск, 2016
Цель работы: ознакомиться с физикой явления поверхностного натяжения; определить коэффициент поверхностного натяжения воды, мыльного и солевого растворов.
Приборы и принадлежности: весы Жоли, кольцо на пружине, разновесы (монетки), линейка, кюветы с различными жидкостями.
ТЕОРИЯ ВОПРОСА
Поверхностное натяжение жидкости
Поверхностное натяжение возникает на границе двух фаз (жидкость - пар, жидкость - жидкость) и обусловлено различием межмолекулярного взаимодействия в этих фазах.
Для увеличения поверхности жидкости надо вывести некоторое количество молекул из глубины на поверхность, т. е. cовершить работу против сил межмолекулярного взаимодействия f. Эта работа пропорциональна увеличению поверхности жидкости. Пусть dA – работа, которую надо совершить, чтобы увеличить площадь поверхности жидкости на dS при постоянной температуре. Тогда:
dA=-σdS
где знак минус обозначает, что для увеличения поверхности совершается внешняя работа. Коэффициент пропорциональности σ называется поверхностным натяжением.
Из вышеуказанной формулы следует, что поверхностное натяжение равно работе, которую нужно совершить, чтобы увеличить поверхность жидкости на единицу. Поскольку молекулы жидкости, находящиеся в поверхностном слое, втягиваются внутрь жидкости, их потенциальная энергия больше, чем у молекул внутри жидкости. Эту дополнительную потенциальную энергию молекул поверхностного слоя жидкости называют свободной поверхностной энергией E. За счет нее может быть произведена работа, связанная с уменьшением поверхности жидкости, причем учитывая закон сохранения энергии:
dA=-dE
При увеличении поверхности жидкости работа, совершаемая внешними силами, идет на увеличение свободной поверхностной энергии поверхностного слоя. Следовательно, увеличение свободной энергии поверхностного слоя равно dE=σdS, откуда свободная поверхностная энергия будет равна:
E=σS
где S - площадь жидкости.
Таким образом, поверхностное натяжение можно также определить как свободную поверхностную энергию единицы поверхности жидкости. При постоянной температуре система стремится к состоянию с минимальной свободной энергией.
Жидкость стремится к такому состоянию, при котором ее поверхность минимальна. Это в свою очередь означает, что должны существовать силы, стремящиеся сократить поверхность жидкости. Эти силы называются силами поверхностного натяжения.
2. Метод отрыва кольца
Для данного метода используется установка для определения величины σ – весы Жоли (изображены слева на рисунке). Далее производятся следующие действия: кольцо опускается в кювету с жидкостью с помощью винта так, чтобы оно слегка коснулось поверхности этой жидкости. Затем кольцо медленно поднимается. При этом на него со стороны жидкости действует силы поверхностного натяжения, приложенные к границе поверхности жидкости и кольца. Поднимая кольцо, пружина будет постепенно растягиваться, и будет увеличиваться сила упругости Fупр пружины. В момент, когда Fупр станет равной силе поверхностного натяжения F (суммарная сила по всей границе жидкости с кольцом), кольцо оторвется от поверхности воды. Измерив удлинение пружины в момент отрыва, можно определить Fупр и, следовательно, и силу поверхностного натяжения F.
Для нахождения поверхностного натяжения используется формула: 
. Граница поверхности жидкости и кольца проходит по внутренней и внешней окружности кольца, т. е. L=πD+πD1, где D и D1 - внутренний и внешний диаметры кольца. Так как D1=D+2h (h - толщина кольца), то
L=2π(D+h)
Это длина контура, ограничивающего поверхность жидкости и кольца. Тогда поверхностное натяжение жидкости определяется по формуле
;
где F - сила поверхностного натяжения, D - внутренний диаметр кольца,
h - толщина кольца.
Ход работы
1) По шкале с помощью указателя определяем начальное положение платформы l0, измерения проводим 3 раза и высчитываем среднее значение <l0>:
l01 =6,6·10-2 (м),
l02 =6,5·10-2 (м),
l03 =6,7·10-2 (м),
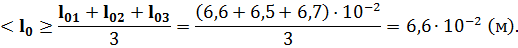
2) На платформу (возле подвески) последовательно кладём грузы (монетки) весом от 1 до 5 Гс (грамм-сила); для каждого определяем положение платформы l. Далее высчитали удлинение пружины ∆l: поскольку <l0>= 6,6·10-2м, а ∆l=l-<l0>, то:
∆l1=l1-<l0>=(6,8-6,6)·10-2=2·10-3 (м),
∆l2=l2-<l0>=(7-6,6)·10-2=4·10-3 (м),
∆l3=l3-<l0>=(7,2-6,6)·10-2=6·10-3 (м),
∆l4=l4-<l0>=(7,4-6,6)·10-2=8·10-3 (м),
∆l5=l5-<l0>=(7,6-6,6)·10-2=10-3 (м).
Все значения заносим в таблицу 1.
Таблица 1 – Измерение зависимости удлинения пружины от деформирующей силы
| <l0>,·10-2 м | P, Гс | l,·10-2 м | ∆l,·10-3 м |
| 6,6 | 6,8 | ||
| 7,2 | |||
| 7,4 | |||
| 7,6 |
3) По полученным данным был построен график зависимости удлинения пружины от веса груза (Рисунок 1).
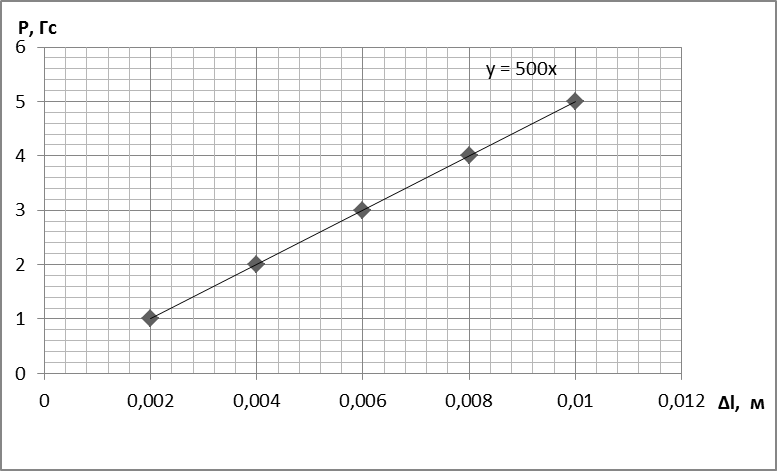
Рисунок 1 – График зависимости удлинения пружины от веса груза
4) Снимаем кольцо и измеряем линейкой внутренний диаметр D =6,95·10-2 м и толщину кольца h =2·10-3 м.
5) Протираем внутреннюю поверхность кюветы и кольцо спиртом. Подвешиваем кольцо обратно.
6) Ставим кювету на столик, наполняем ее дистиллированной водой. Опустим кольцо с помощью винта так, чтобы поверхность воды коснулась кольца. Медленно поднимая кольцо с помощью микрометрического винта, зафиксируем по шкале положение платформы l в момент отрыва кольца. Измерения проведены 5 раз и найдено среднее значение <l> и удлинение <∆l> пружины в момент отрыва кольца.
l1 =7,2·10-2 (м),
l2 =7,1·10-2 (м),
l3 =7,3·10-2 (м),
l4 =7,2·10-2 (м),
l5 =7,1·10-2 (м),
Тогда <∆l>=<l>-<l0> =(7,18-6,6)·10-2=5,8·10-3 (м).
7) Теперь, зная удлинение пружины, по графику зависимости удлинения пружины от веса груза (см. рисунок 1) можно определить деформирующую силу, которая вызывает данное удлинение <∆l>, то есть силу поверхностного натяжения F. Согласно этому графику, а точнее, уравнению линии тренда рисунка
y=500x
при этом x=<∆l> =5,8·10-3 м, отсюда y =5,8*10-3*500=2,9 Гс, что соответствует весу P. Так как 1 Гс=9,8·10-3 Н, то сила поверхностного натяжения будет равна:
F =2,9·9,8·10-3=2,84·10-2 (Н)
8) Рассчитаем поверхностное натяжение по формуле:
9) Если принять, что в данном опыте температура равна 20° С, то
σтабл= 7,275·10-2 (Н/м)
Отсюда вычислим относительную погрешность:
Все значения по дистиллированной воде занесены в таблицу 2.
Таблица 2 – Измерение поверхностного натяжения в дистиллированной воде
| D,10-2м | h,10-3 м | <l>,102м | <∆l>, 10-3 м | F,10-2 H | σ,10-2 Н/м | °C | σтабл, Н/м | ε, % |
| 6,95 | 7,18 | 5,8 | 2,84 | 6,32 | 7,275 | 13,12 |
Аналогичные измерения были проведены с солевым и мыльным раствором.
10) Для солевого раствора (конкретнее, раствора соды)
<∆l1>=<l1>-<l0> = (7,32-6,6)*10-2= 7,2*10-3 м.
y = 500x = 7,2*10-3*500 = 3,6 Гс
F1 =3,6·9,8·10-3=3,528·10-2 (Н)
11) Для мыльного раствора
<∆l2>=<l2>-<l0> =(6,7-6,6)·10-2=1·10-3 (м);
y = 500x = 1*500*10-3 = 0,5 Гс
F2 =0,5·9,8·10-3=0,49·10-2 (Н)
Все результаты по растворам соды и мыла приведены ниже в таблице 3.
Таблица 3 – Поверхностное натяжение в солевом и мыльном растворе
| Солевой раствор | Мыльный раствор | ||||||
| <l1>,10-2 м | <∆l1>,10-3 м | F1,10-2 H | σ1,10-2 Н/м | <l2>, 10-2 м | <∆l2>, 10-3 м | F2,10-2 H | σ2,10-2 Н/м |
| 7,32 | 7,2 | 3,528 | 7,85 | 6,7 | 0,49 | 1,09 |
Вывод
Методом отрыва кольца было исследовано поверхностное натяжение воды, мыльного и солевого растворов. Определены коэффициенты пропорциональности вышеуказанных жидкостей, то есть их поверхностное натяжение σ.
Мы выяснили, что коэффициент поверхностного натяжения дистиллированной воды составил σ =6,32·10-2 Н/м. Относительная погрешность составила 13,12 %. Причины её появления в первую очередь связаны с методикой проведения исследований (посуда могла быть недостаточно чистой, а положение кольца в установке было неровным), а также неточностью измерительных приборов (например, шкалы с делениями весов Жоли).
Мыло и соль (сода) по отношению к воде являются примесями, поэтому поверхностное натяжение дистиллированной воды отличается от поверхностных натяжений мыльного и солевого растворов.
Растворение соли в воде повышает поверхностное натяжение
(σ =7,85·10-2 Н/м), поскольку молекулы соли взаимодействуют с молекулами жидкости сильнее, чем молекулы жидкости между собой. В промышленности мыло «высаливают» из растворов именно на основании свойств соли при растворении повышать поверхностное натяжение.
Напротив, растворение мыла понижает поверхностное натяжение (σ =
=1,09·10-2˚Н/м). Это происходит, потому что силы притяжения между молекулами самой жидкости больше сил притяжения между молекулами жидкости и примеси, поэтому молекулы жидкости, расположенные в поверхностном слое, с большей силой втягиваются внутрь жидкости, чем молекулы примеси. Таким образом, молекулы жидкости уходят из поверхностного слоя вглубь жидкости, а молекулы мыла вытесняются на поверхность. Вещества, понижающие поверхностное натяжение, называются поверхностно активными и находят широкое применение в быту.
