Лабораторная работа 2
Представление чисел
В позиционных системах счисления
Теоретическое обоснование
Совокупность приемов наименования и записи чисел называется системой счисления. Счисление представляет собой частный случай кодирования, где слово, записанное с использованием определенного алфавита и по определенным правилам, называется кодом. Если значение цифры или символа зависит от позиции в ряду цифр или символов изображающих число, то такая система счисления называется позиционной, в противном случае - непозиционной системой.
В любой системе счисления выбирается алфавит, представляющий собой совокупность некоторых символов (цифр или знаков), с помощью которого можно представить любое число. Если алфавит состоит из двух цифр 0 и 1, то система двоичная. В десятичной системе алфавит состоит из десяти цифр: 0, 1, 2, …, 9. В восьмеричной - из восьми: 0, 1, 2, …,7. В шестнадцатеричной - используется десять цифр 0, 1, 2,…,9 и буквы латинского алфавита A (обозначает цифру 10), B (11), C(12), D(13), E(14), F(15). Количество используемых цифр называется основанием позиционной системы счисления. Место для цифры в числе называется разрядом, а количество цифр в числе - разрядностью числа. Крайняя слева цифра называется цифрой старшего разряда, а крайняя справа - младшего разряда.
Алгоритм перевода чисел из 10-й системы в Р-ю (Р-целое, положительное число):
1) Целая и дробная части числа переводятся отдельно.
2) Целая часть числа последовательно делится нацело на величину Р и остатки от деления записываются, начиная с последнего как результат.
3) Дробная часть числа последовательно умножается на Р и целые значения записываются, начиная с первого как результат. Умножение выполняется до получения в дробной части 0 или с указанной точностью (по умолчанию – 6 знаков после запятой).
Пример: Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

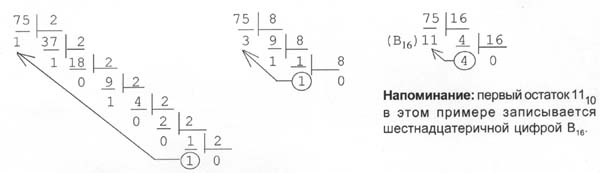
Ответ: 7510 = 1 001 0112 = 1138 = 4B16.
Для перевода правильной десятичной дроби F в систему счисления с основанием q необходимо F умножить на q, записанное в той же десятичной системе, затем дробную часть полученного произведения снова умножить на q, и т. д., до тех пор, пока дробная часть очередного произведения не станет равной нулю, либо не будет достигнута требуемая точность изображения числа F в q-ичной системе. Представлением дробной части числа F в новой системе счисления будет последовательность целых частей полученных произведений, записанных в порядке их получения и изображенных одной q-ичной цифрой. Если требуемая точность перевода числа F составляет k знаков после запятой, то предельная абсолютная погрешность при этом равняется q -(k+1) / 2.
Пример. Переведем число 0,36 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Для чисел, имеющих как целую, так и дробную части, перевод из десятичной системы счисления в другую осуществляется отдельно для целой и дробной частей по правилам, указанным выше.
Перевод из Р-й системы в 10-ю (Р - целое, положительное число):
Любое число Х в позиционной системе счисления P можно представить в виде ряда:

где ХР – запись числа в системе счисления с основанием Р; хi - целое положительное число, меньше Р; n – число разрядов в целой части числа;
m – число разрядов в дробной части числа.
Такая схема называется схемой Горнера.
Алгоритм перевода из Р-й системы в 10-ю:
1) От запятой вправо и влево нумеруются разряды чисел.
2) Каждая цифра числа хi умножается на основание системы Р в степени номера разряда, результаты складываются.
Пример. Переведем числа, записанные в двоичной, восьмеричной и шестнадцатеричной системах счисления, в десятичную.
Перевод из 2-й в 10-ю систему:
Разряды 3 2 1 0 -1
Число 1 0 1 1,  =1*
=1*  .
.
Из 8-й системы в 10-ю:
Разряды 2 1 0 -1 Число 2 7 
Из 16-й системы в 10-ю:
Разряды 2 1 0 Число 1 F 
Пример.
В системе счисления с некоторым основанием десятичное число 18 записывается в виде 30. Укажите это основание.
Решение:
Примем за х основание неизвестной системы счисления. Пронумеруем разряды и запишем данные числа в развёрнутой форме:

Ответ: десятичное число 18 записывается в виде 30 в системе счисления с основанием 6.
Задания:
1) Среди чисел 100011002, 2218, 9616 какие меньше 14610 и почему?
2) Переведите числа 101,8 и 200,6 в 2-ю, 8-ю, 16-ю системы с точностью до 4-х знаков после запятой. Полученные результаты переведите в 10-ю систему.
3) Равенство 14+3=22 будет истинным в системе счисления с основанием 7, 5, 10 или 2?
4) Определите, в какой системе счисления записано математическое выражение 122+2=201?
Перевод из 8-й (16-й) системы счисления в 2-ю систему
Так как 8=23 и 16=24, то перевод чисел из 8-й (16-й) системы счисления в 2-ю можно упростить. Каждую 8-ю (16-ю) цифру надо перевести в 2-й вид и представить тремя (четырьмя) разрядами в соответствии с таблицей 1.
Таблица 1- Таблицы соответствия чисел 2-й и 8-й (16-й) систем
| 8-е цифры | 2-е числа | 16-е цифры | 2-е числа | 16-е цифры | 2-е числа | |
| А(10) | ||||||
| В(11) | ||||||
| С(12) | ||||||
| D(13) | ||||||
| E(14) | ||||||
| F(15) |
Пример 3. Перевести числа 265,128 и С4В,2516 в 2-ю систему счисления.
| 265,128= | 101, | 0102 | =10110101, 001012. | |||||||||
| 5, | ||||||||||||
| С4В,2516= | 1011, | 01012 | =110001001011, 001001012. | |||||||||
| C | B, | |||||||||||
Справедливо и обратно: для перевода из 2-й системы в 8(или 16) - ю число от запятой в право и влево разделяется по три (для 8-й системы) или четыре (для 16-й системы) разряда. При недостатке разрядов исходное число дополняется слева или справа нолями, что не меняет его величину. Полученные таким образом двоичные числа записываются по таблице 1 как 8-е или 16-е числа. Например:
| 10110101, 001012= | 101, | 0102 | =265,128. | |||||||||
| 5, | ||||||||||||
| 110001001011, 001001012= | 1011, | 01012 | = С4В,2516 | |||||||||
| C | B, | |||||||||||
Задания:
1) Записанное в 16-й системе число 3F, С в 2-й системе с точностью до 2-х знаков после запятой, это: 111111, 112; 1111111,012; 111101,102 или 111110,102? Выберите правильный ответ.
2) Записанное в 2-й системе счисления число 100011,112 какой вид будет иметь в 16-й системе с точностью до 2-х знаков после запятой?
3) Среди чисел 101100002, 16710, AF16 сколько чисел меньше числа 2618 ?
Двоичная арифметика.
Правила выполнения арифметических действий над двоичными числами задаются таблицей 2.
Таблица 2 – Правили выполнения арифметических операций
| Двоичное сложение | Двоичное вычитание | Двоичное умножение |
| 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10 | 0 – 0 = 0 1 - 0 = 1 1 – 1 = 0 10 - 1 = 1 | 0  0 = 0 0 0 = 0 0  1 = 0 1 1 = 0 1  0 = 0 1 0 = 0 1  1 = 1 1 = 1
|
При сложении двоичных чисел в каждом разряде производится сложение цифр слагаемых и переноса из соседнего младшего разряда, если он имеется. При этом необходимо учитывать, что 1+1 дают ноль в данном разряде и единицу переноса в следующий.
 Пример. Выполнить сложение двоичных чисел: X=1101, Y=101.
Пример. Выполнить сложение двоичных чисел: X=1101, Y=101.
При вычитании двоичных чисел в данном разряде при необходимости занимается 1 из старшего разряда.
Пример. Даны двоичные числа X=10010 и Y=101. Вычислить X-Y.

Умножение двоичных чисел производится по тем же правилам, что и для десятичных с помощью таблиц двоичного умножения и сложения. Для удобства вычислений рекомендуется складывать по два слагаемых, а затем к полученной сумме прибавлять следующее слагаемое (пример 1.6 а))
Пример. Даны двоичные числа X и Y, вычислить X  Y.
Y.

 а) X=1001 и Y=101
а) X=1001 и Y=101
б) X=1001 и Y=111
Для выполнения деления двоичных чисел используются таблицы двоичного умножения и вычитания.
Пример. Даны двоичные числа X=1100.011 и Y=1001. Вычислить X/Y.

Задания
1. Для каждого из чисел определить разрядность и указать номера старшего и младшего разрядов: а) 12345.034; б) 365; в) -273.1.
2. Представить в виде полинома числа:
а) 51.1510; б) 10110.1012; в) 37.48; г) А7.1Е16.
3. Даны двоичные числа X и Y. Вычислить X+Y и X-Y, если:
а) X=1101001; Y=101111;
б) X=101110110; Y=10111001;
в) X=100011001; Y=101011.
4. Даны двоичные числа X и Y. Вычислить X*Y и X/Y, если:
а) X=1000011011; Y=1011;
б) X=100101; Y=110;
в) X=100000; Y=101.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое система счисления?
2. В чем отличие позиционной системы счисления от непозиционной?
3. Что называется основанием и алфавитом системы счисления?
4. Как порождаются целые числа в позиционных системах счисления?
5. Почему люди пользуются десятичной системой, а компьютеры – двоичной?
6. Почему в компьютерах используются также восьмеричная и шестнадцатеричная системы счисления?
7. Как перевести целое число из десятичной системы в любую другую позиционную систему счисления?
8. Как перевести правильную десятичную дробь в любую другую позиционную систему счисления?
9. Как перевести число из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную?






