Калибровочные кривые. При конструировании многих физических измерительных приборов часто используются физические явления, позволяющие судить об одной физической величине, тогда как в действительности измеряется совершенно другая физическая величина. Так, например, по потенциалу, создаваемому термопарой, можно судить о разности температур ее спаев; по величине угла вращения плоскости поляризации поляризованного света можно судить о концентрации некоторых веществ в растворе и т.д.
В этом случае возможны два варианта оформления шкалы прибора: или проградуировать шкалу прибора сразу в единицах той физической величины, которую мы хотим измерять с помощью нашего прибора, или оставить шкалу в единицах непосредственно измеряемой величины и снабдить его так называемой калибровочной кривой, которая позволяла бы графически пересчитывать показания прибора в значениях нужной нам физической величины.
Так, шкала вольтметра, включенного в термопару, может быть сразу проградуирована в градусах, и хотя вольтметр измеряет напряжение, генерируемое термопарой в вольтах, снимать с него измерения мы будем в градусах. Приведем некоторые соображения, свидетельствующие о необходимости строить калибровочные кривые на примере создания термопары.
Для создания термопары прежде всего необходимо выбрать разнородные проводники (или полупроводники) таким образом, чтобы их контакт приводил к максимально возможно высокому уровню генерируемого потенциала. Далее производится спайка концов термопары. В процессе этой работы невозможно учесть все сопутствующие этим процессам постоянные (однородность и чистоту выбранных проводников, качество спайки и другие). В результате фактически получается уникальный прибор, который в любом случае необходимо тарировать (то есть сравнивать с эталоном). Однако эталон не всегда находится в пределах достижимости. В этом случае и производят калибровку прибора.
Как строятся калибровочные кривые? Сначала фиксируют диапазон, в котором может изменяться физическая величина, подлежащая измерению. Например, если мы планируем измерять с помощью термопары температуру тела человека (в том числе и поверхностную), то диапазон может быть выбран от 15 градусов (замершие руки) до 42 градусов (максимальная температура центральной области тела больного человека). После этого решается задача выбора точек, в которых будет происходить сравнение показаний термопары с температурой среды, которая заранее известна и поддерживается с максимальной достижимой точностью. Ясно, что чем больше мы таких сред создадим, тем больше получим точек калибровочной кривой и с тем большей точностью в будущем будем измерять температуру данной термопарой. Однако создание сред со строго фиксированной температурой и поддержание этой температуры на постоянном уровне - сложная инженерная задача. Поэтому и необходим компромисс: с одной стороны, необходимо как можно больше точек калибровки, а с другой - создание слишком большого количества точек калибровки требует значительных усилий. Часто (как в случае с термопарой) выбор количества точек калибровки может быть существенно ограничен, если мы знаем теоретическую функциональную зависимость между непосредственно измеряемой величиной и величиной, которую мы планируем измерять с помощью данного прибора. В случае термопары такая зависимость известна:
(7).
Здесь V – показания вольтметра в милливольтах, k – коэффициент пропорциональности (постоянная термопары), t2 и t1 – температура сред, в которые помещены второй и первый спаи термопары. Соотношение (7) говорит нам, что зависимость между показаниями вольтметра и разностью температур линейная. Это значит, что в предельном случае нам нужно только две точки калибровки, а калибровочная кривая представляет собой прямую линию, соединяющую эти точки. Однако для получения калибровочных точек нам надо проводить измерения и, следовательно, они будут получены с определенной ошибкой. Чтобы уменьшить эту ошибку, обычно проводят построение не двух калибровочных точек, а 5–6, равномерно распределенных по всему диапазону возможного изменения изучаемой физической величины (в данном случае, как указывалось выше, диапазон составляет от 15 до 42 градусов).
Перейдем к конкретному описанию калибровочной кривой для нашего случая. Допустим, у нас уже есть термопара, надо ее откалибровать. Подготовим первую пробу (сосуд с водой), доведем ее температуру до 5 градусов, затем поместим в очень хороший термостат (напомним, что точка в 5 градусов выбрана так далеко от нужного нам диапазона, исходя из правила: старайся не измерять в начале шкалы!). Далее подготовим еще шесть проб с точно фиксированными температурами: 15, 20, 25, 30, 35 и 40 градусов. Здесь также возникнет достаточно трудная задача – поддержание температуры проб на одном уровне. Допустим, мы с ней справились. Проведем измерения, по очереди опуская второй спай термопары в каждую из проб и фиксируя в каждом случае показания вольтметра. Допустим, мы получили следующие значения: 2,5; 4,3; 5,9; 7,2; 8,1; 9,3 милливольт. Итак, в результате мы получим два ряда чисел: ряд температур в градусах Цельсия и соответствующий ряд показания вольтметра в милливольтах. Отложив показания вольтметра по оси абсцисс, а температуру - по оси ординат получим следующий график:
Рис. 1.
Из рис.1 видно, что точки с небольшими отклонениями располагаются вдоль некоторой прямой. Поэтому можно считать, что уравнение (7) вполне удовлетворительно описывает связь между температурой второго спая и показаниями вольтметра. Осталось рассчитать параметры искомой прямой.
Поскольку уравнение прямой имеет вид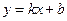 
, нашей задачей является по имеющимся экспериментальным точкам рассчитать оценки к и b. Существуют две наиболее часто применяемые расчетные процедуры, позволяющие это сделать. Первая называется метод наименьших квадратов, вторая - метод максимального правдоподобия. Точное описание этих процедур выходит за рамки нашего изложения. Отметим только два положения. Во-первых, эти процедуры есть практически в любом статистическом пакете обработки экспериментальных данных (Статистика, SPSS и другие), во-вторых, метод наименьших квадратов имеет простую геометрическую интерпретацию: наилучшей считается такая кривая (в нашем случае прямая), сумма квадратов отклонений экспериментальных точек от которой является минимальной. Проведя расчет параметров прямой по одному из указанных выше методов, мы получим возможность нарисовать следующий рисунок (рис. 2):
Рис. 2.
Линия, изображенная на рис. 2, является калибровочной кривой (в нашем случае – прямой). Приведем пример использования калибровочной кривой. Допустим, мы создали водную среду точно с температурой 5 градусов, термостабилизировали ее и поместили в нее один из спаев термопары. Второй спай поместим в среду, температура которой неизвестна. Снимем показание вольтметра. Пусть оно оказалось равным 3,5 милливольта. Проведем построение, изображенное на рис. 3.
Рис. 3.
Из рис. 3 видно, что показанию милливольтметра, равному 3,5 милливольт, приблизительно соответствует температура 18,5 градусов.
В данном случае мы ставили перед собой задачу описать только общие принципы построения калибровочных кривых. Термопара была выбрана в качестве наиболее простого примера для иллюстрации общих принципов построения таких кривых. Более подробно и полно с калибровкой термопары можно будет ознакомиться во время проведения соответствующей лабораторной работы.
Графическое представление данных. Во многих лабораторных работах оказывается удобным изображать графически зависимость между изучаемыми величинами. Для того чтобы построить график, необходимо на основании проделанных измерений составить таблицу, в которой каждому значению одной из величин соответствует определенное значение другой.
Допустим, мы получили следующую таблицу:
| Xi (с) | ||||||||
| Yi (мА) |
При построении графика значения независимой переменной следует откладывать на оси абсцисс, а значения функции - на оси ординат. Около каждой оси нужно написать обозначение откладываемой величины и указать, в каких единицах она выражена. Для правильного построения графика важным является выбор масштаба. Масштаб по каждой оси может быть каким угодно. Стараются всегда выбирать масштаб так, чтобы график занял весь лист и его размеры по обеим осям получались приблизительно одинаковыми. При этом следует иметь в виду, что пересечение координатных осей не обязательно должно совпадать с нулевыми значениями х и у. При выборе начала координат следует руководствоваться тем, чтобы полностью использовать всю площадь чертежа. Приведем пример неправильно построенного графика:
Рис. 4
Как видно из рис. 4, здесь допущены сразу две ошибки: неправильно выбрана точка пересечения осей координат и неправильно выбран масштаб оси ординат. Исправить эти ошибки можно следующим образом.
Рис. 5.
Совершенно очевидно, что график, представленный на рис. 5, анализировать значительно легче, чем график, представленный на рис. 4.
Когда масштаб и начало координат выбраны, приступают к построению графика. На основании данных таблицы наносят на координатную плоскость точки. Если можно определить абсолютные погрешности измерений 
и 
, то их откладывают по обе стороны точки в виде креста так, чтобы точка оказалась в центре креста.
Если нет возможности по тем или иным обстоятельствам построить кривую наилучшим образом, аппроксимирующим экспериментальные точки с помощью метода наименьших квадратов или максимального правдоподобия, то между точками проводят прямую или плавную кривую линию, проходящую через интервалы абсолютных погрешностей так, чтобы возможно больше точек легло на эту линию, а остальные распределились равномерно выше и ниже ее.
Построенный график позволяет выявить те измерения, которые были выполнены плохо или неверно. Если какая-либо точка сильно выпадает из графика, ее следует отбросить, а данное измерение проверить на промах.
Пользуясь графиком, можно также в пределах проведенных измерений интерполировать, иначе говоря, находить значение величины у для таких значений х, которые непосредственно не наблюдались. Для этого из любой точки оси абсцисс (или ординат) надо провести ординату (или абсциссу) до пересечения с графиком. Длина этой ординаты (или абсциссы) будет представлять собой значение у соответствующего значения х (как это делалось после построения калибровочной кривой (см. рис. 3).
Часто при построении графиков на осях координат откладывают не сами величины, а их функции (квадраты, логарифмы и т.п.). Дело в том, что экспериментальные точки никогда не укладываются точно на одной кривой, всегда имеется разброс точек. Проще всего построить график, если искомая зависимость имеет линейный характер. Не представляет труда провести через экспериментальные точки наилучшую прямую, но значительно труднее провести наилучшую кривую линию. Для некоторых нелинейных зависимостей масштаб по осям можно выбрать так, что график будет иметь вид прямой линии.
Очень часто для выпрямления графиков используют полулогарифмические и логарифмические шкалы. Полулогарифмическая система координат – это прямоугольная система, по одной оси которой равномерный масштаб, а по другой – логарифмический (пропорциональный логарифму натуральных чисел). Примером логарифмического масштаба является основная шкала логарифмической линейки.
Полулогарифмическая система координат очень удобна для построения графиков показательных функций типа:
(8).
Действительно, lg y =lg a ± k(lg e) x. Пусть lg y=Y; lg a=A; k lg e=B. Тогда наша зависимость в новых координатах будет выглядеть:
Y =А+Вх (9).
Если построить график зависимости Y от x, то он будет представлять собой прямую линию.
Логарифмическая система координат – это такая система координат, на обеих осях которой отложены логарифмические масштабы. Логарифмическая система координат очень удобна для изображения графика степеней функций типа:
(10).
Действительно, если опять прологарифмировать уравнение (10) и ввести новые переменные, то мы получим: lg y=lg a±k lg x. Пусть lg y=Y; lg a=A; lg x=X.
Тогда мы получаем опять уравнение прямой:
Y=A+kX. (11).
Приведем пример, иллюстрирующий введение полулогарифмической системы координат.
Допустим, мы наблюдаем за процессом размножения бактерий во времени. Из курса физики мы знаем, что этот процесс описывается экспоненциальной кривой. Проведя измерения, мы получили следующую таблицу (напомним, что мы описываем мысленный эксперимент, исключительно для иллюстрации метода):
| Xi (мин) | |||||||
| Yi (штук) |
Допустим, что мы провели аппроксимацию полученных экспериментальных точек экспоненциальной кривой по методу наименьших квадратов и нанесли полученные результаты на график:
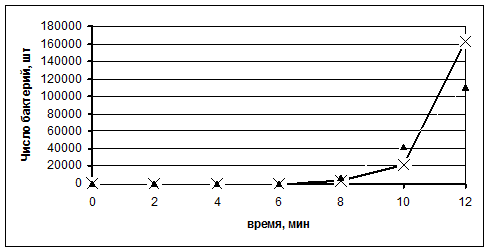
Рис.6
На этом рисунке символом ▲ помечены значения, полученные в эксперименте, символом 
помечены соответствующие значения аппроксимирующей кривой.
Как видно из рисунка, заметные различия между экспериментальными точками и точками аппроксимирующей кривой начинают визуально наблюдаться только в конце диапазона измерений. Это неудобно. Введем логарифмическую шкалу по оси ординат, тогда получим следующий график:
Рис.7
Обозначения на рис. 7 те же, что и на рис. 6. Очевидно, что анализировать зависимость по этому графику значительно проще.
Контрольные вопросы
- Что понимают под измерением физической величины?
- Что называется погрешностью физической величины?
- Типы ошибок (систематические, случайные и промахи).
- Абсолютная и относительная погрешности измерения.
- Истинное значение измерения физической величины.
- Графические методы обработки результатов измерений.
Лабораторная работа №1
