По своему положению в пространстве прямые делятся на прямые общего и частного положения. Прямые частного положения на прямые уровня и проецирующие прямые.
Проецирующие прямые являются и прямыми уровня. Фронтально-проецирующая прямая является и горизонталью и профильной прямой, поскольку она параллельна и горизонтальной и профильной плоскостям проекций. По этой же причине горизонтально-проецирующая прямая и фронталь и профильная прямая, к профильно-проецирующая прямая – горизонталь и фронталь. Следовательно, проецирующие прямые одновременно дважды прямые уровня.
Практическое занятие №3.
(модуль «Поверхности и аксонометрические проекции»)
Тема: Поверхности и плоскости.
Цель занятия: Изучение проецирующих и непроецирующих поверхностей; их сходства и различия, принадлежность точки и прямой поверхности. Параллельность прямой и плоскости, параллельность плоскости.
Продолжительность занятия: 6 часов.
Вопросы для подготовки к занятию:
1) Что называется определителем поверхности?
2) Что называется пирамидой?
3) Какие поверхности называются линейчатыми?
4) Назовите способы задания поверхности?
5) Сформулируйте признак параллельности прямой и плоскости; признак параллельности плоскости.
Задача №1.
Построить недостающие проекции точек на поверхности цилиндра.
Методические рекомендации по выполнению задания.
Цилиндр является проецирующей поверхностью, т.е. все точки, лежащие на боковой поверхности цилиндра спроецируются по линиям связи на очерк, т.е. на окружность. Точка А – видимая, потому она проецируются на часть окружности, расположенную перед очерковыми образующими. Точка В – невидимая, следовательно, она проецируется на часть окружности за очерковыми образующими. Точка С расположена на верхнем основании цилиндра, таким образом, проецируем точку С с П1 на П2 по линии связи.
Задача №2.
Построить три проекции точки А на конической поверхности.
Методические рекомендации по выполнению задания.
Проекция точки А имеется только на фронтальной плоскости проекции. Чтобы построить проекцию точки А на горизонтальной плоскости замерим радиус параллели, на которой расположена А2, и построим вторую проекцию параллели (окружность) на П1, затем по линии определяем проекцию А1. Для построения проекции точки А на П3 замеряем расстояние y на П1 и переносим данное расстояние по линии связи на П3.
Задача №3.
Через точку К провести плоскость, параллельную прямой m.
Даны плоскость m (m1; m2) и точка К (К1; К2). Чтобы провести через К плоскость 
параллельную прямой, достаточно изобразить на комплексном чертеже проходящие через точку К фронтальную а 2, и горизонтальную а 1 проекции прямой а, параллельные соответствующим проекциям заданной прямой m, а далее провести через т. К произвольную прямую b (решений бесконечное множество).
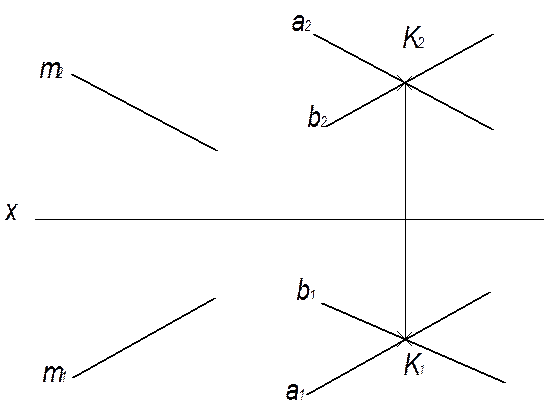
Индивидуальное задание №1.
Найти недостающие проекции точек на поверхности гранных тел.
Индивидуальное задание №2.
Построить недостающие проекции точек на поверхностях вращения.
Индивидуальное задание №3.
Через точку К провести плоскость , параллельную плоскости Г, заданной двумя пересекающимися прямыми n и m.
Отчет по практическому занятию.
По практическому занятию можно сделать следующие выводы:
1. Главная проекция прямой, плоскости или поверхности – проекция вырожденная (прямой – в точку; плоскости – в прямую линии; поверхности – в ее основание).
2. Основное свойство главной проекции проецирующего образа состоит в том, любая точка или линия, принадлежащие прямой, плоскости или поверхности, одной из проекций будут иметь проекцию точки либо линии, совпадающие с главной проекцией прямой, плоскости или поверхности.
3. Проецирующими образами являются только прямая, призма или цилиндр.
Практическое занятие №4.
(модуль «Поверхности и аксонометрические проекции»)
Тема: «Графопозиционные задачи».
Цель занятия: Изучить правила построения линии пересечения двух поверхностей.
Продолжительность занятия: 16 часов.
Вопросы для подготовки к занятию:
1) Алгоритм построения линии пересечения прямой и плоскости.
2) К чему сводится задача на построение линии пересечения гранного геометрического тела с телом вращения.
3) Какая фигура получается при пересечении призмы плоскостью.
4) В каких случаях применяются в качестве посредников плоскости?
5) Когда применяются сферы посредников?
Задача №1.
Построить проекцию линии пересечения двух плоскостей общего положения. Для решения этой задачи рассмотрим две плоскости, заданные проекциями треугольников АВС и КЕД.
В плоскости 
КЕД заключим прямую КД в проецирующую плоскость-посредник . Тогда плоскость пересекает СВ в т.1, а СА – в точке 2. Найдем проекции т.1 и 2 на горизонтальной плоскости проекций. Соединив 11 и 21 , находим F1 – точку пересечения прямой 1, 2 с КД на горизонтальной плоскости проекций. Спроецируем F на П2.
Аналогичным образом определим т.G, заключив АВ в проецирующую плоскость Г. Соединив т. F и G, получим проекцию линии пересечения.
Видимость сторон треугольника определяем методом конкурирующих точек отдельно для горизонтальной и фронтальной плоскостей проекций.
Даны плоскости: (А, В, С); Т (D, Е, К).
Построить линию пересечения плоскостей MN = 
Т.
Чтобы рассмотреть задачу на пересечение двух плоскостей, необходимо решить 1 ГПЗ, т.е. задачу, рассматривающую пересечение прямой с плоскостью. В поставленной перед нами задаче необходимо определить линию пересечения двух треугольников, для этого достаточно иметь две общие для этих плоскостей точки. Поэтому линия пересечения треугольников строится по точкам пересечения стороны АВ одного треугольника АВС с плоскостью другого треугольника Т (DEK). А также стороны ED с плоскостью (АВС).
Задача №2.
Построить проекции линии пересечения пирамиды ABCD и призмы EKGV.
По данным координатам точек A, B, C, D строим проекции пирамиды ABCD с вершиной D и призмы EKGV.
Поверхность призмы является горизонтально-проецирующей, поэтому горизонтальная проекция линии пересечения призмы и пирамиды уже имеется. Она совпадает с горизонтальной проекцией призмы.
Нахождение фронтальной проекции сводится к построению точки пересечения прямых (ребер одной поверхности) с плоскостями (гранями другой поверхности); и к построению линии пересечению плоскостей (граней поверхностей).
Отмечаем горизонтальные проекции точек 1, 2, 3 – пересечения ребер пирамиды с гранью GV – призмы. По линиям связи находим фронтальные проекции точек, которые будут располагаться на соответствующих фронтальных проекциях ребер. Аналогично строим фронтальные проекции точек 4, 5, 6.
Отмечаем горизонтальные проекции 7, 8 пересечения ребра Е призмы гранями пирамиды. Они будут совпадать с горизонтальной проекцией т. Е.
Фронтальные проекции т. 7, 8 строим по их принадлежности к граням пирамиды. Для чего проведем через них прямые D-9; D-10.
Соединяем полученные проекции точек отрезками прямых с учетом их расположения на П1. Видимость определяем методом конкурирующих точек.
Задача №3.
Построить проекции линии пересечения тора и треугольной призмы.
Так как грани призматического отверстия перпендикулярны фронтальной плоскости проекций, то треугольник А2В2С2 является уже известной проекцией линии пересечения на П2. Для построения горизонтальных проекций точек А, В и С линии пересечения через фронтальные проекции этих точек проводятся проекции параллелей, которые затем строятся на горизонтальной плоскости проекций как окружности.
Положение проекций точек А, В, С на горизонтальной плоскости проекций определяется на пересечении линий связи с проекциями параллелей. Проекции промежуточных точек 1, 2, 3, 4 строятся аналогично.
Задача №4.
Построим проекции линии пересечения правильной шестиугольной призмы и конуса. Так как боковые грани призмы перпендикулярны профильной плоскости, то проекциями линий перехода на виде слева будут стороны шестиугольника. Поэтому любая точка этого шестиугольника может рассматриваться как известная профильная проекция точки, принадлежащей линии перехода (для большей наглядности объяснений конус достроен до полного). Линия перехода будет состоять из участков гипербол, так как грани призмы параллельны оси конуса. Проекции характерных точек А, лежащих в пересечении ребер призмы с поверхностью конуса, определяются при помощи параллели конуса а. Характерные точки В построены при помощи параллели b – окружности, вписанной в шестиугольник на виде слева.
Промежуточные точки 1 гипербол строятся при помощи параллели с. Через произвольно выбранную точку 13 (профильная проекция точки 1) проводится профильная проекция параллели, положение которой на видах спереди и сверху определяется с помощью точки, расположенной на главном фронтальном меридиане. Фронтальные и горизонтальные проекции точек 1 находятся на пересечении линий связи с проекциями параллели на соответствующих видах. Завершается построение соединением полученных проекций точек в гиперболы при помощи лекала.
Задача №5.
Построить фронтальную проекцию линии пересечения между проекциями цилиндра и конуса.
При этом оси поверхностей пересекаются в точке О и параллельны фронтальной плоскости проекций.
Проведем сферу с центром О так, чтобы она пересекала и цилиндр, и конус. Проведенная сфера будет пересекать поверхность цилиндра по окружности а, которая проецируется в отрезок прямой, соединяющий точки пересечения очерковых линий сферы и цилиндра. Сфера будет пересекать поверхность конуса по двум окружностям b и c, которые спроецируются в отрезки прямых, соединяющих точки пересечения очерковых линий сферы и конуса. Окружность а пересечет окружность b в точке 1, окружность с в точке 2, которые принадлежат линии пересечения цилиндра и конуса.
Для построения проекций точек линии перехода годится не любая сфера. Самая минимальная сфера должна касаться одной из поверхностей и пересекать вторую. С помощью такой сфера построена проекция характерной точки А.
Так как оси цилиндра и конуса параллельны фронтальной плоскости проекций, то точки пересечения проекций главных фронтальных меридианов (В2 и С2) также принадлежат проекции линии пересечения.
Индивидуальное задание №1.
Построить проекции линии пересечения призмы и трехгранной пирамиды.
Индивидуальное задание №2.
Построить проекции линии пересечения сферы и призмы.
Индивидуальное задание №3.
Построить проекции линии пересечения двух поверхностей.
Индивидуальное задание №4.
Построить проекции линии пересечения двух поверхностей.
Отчет по практическому занятию.
В ходе выполнения практического занятия изучены основные случаи построения линии пересечения.
Практическое занятие №5.
(модуль «Способы преобразования чертежа)
Тема: Метрические задачи.
Цель занятия: Изучить способы определения натуральной величины отрезка прямой и плоской фигуры. Наклонность сечения.
Продолжительность занятия: 6 часов.
Вопросы для. Подготовки к занятию.
1). Сколько преобразований необходимо для определения натуральной величины плоской фигуры?
2). Как располагается новая ось относительно проекций отрезка прямой при определении натуральной величины отрезка?
3). Как располагается плоскость проекций относительно прямой при определении натуральной величины отрезка?
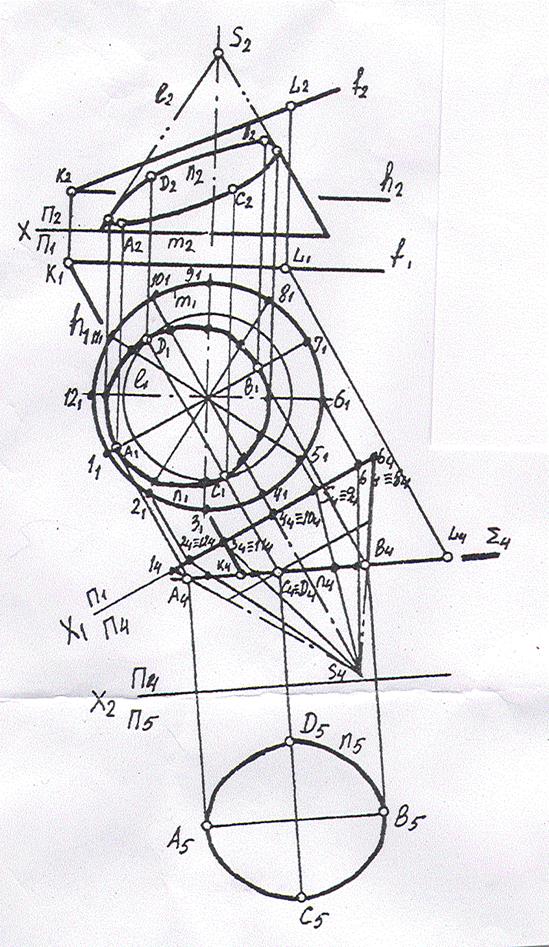
Задача №1.
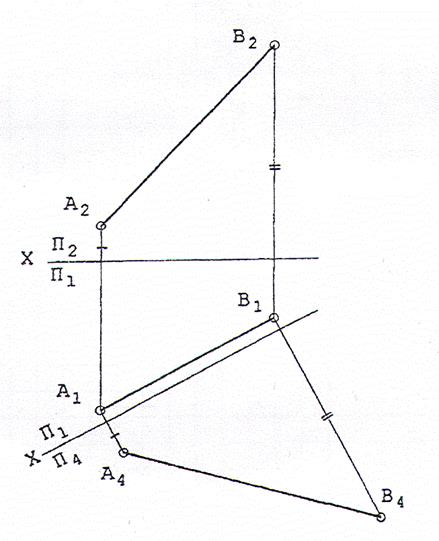
Преобразовать прямую общего положения (АВ) в прямую уровня. Для решения задачи введем новую фронтальную плоскость проекций П4, расположенную параллельно горизонтальной проекции А1В1 прямой (АВ). Т.к. при проведении новой фронтальной плоскости проекций координаты Z точек А и В не изменяются, дальнейшие построения ясны из чертежа, причем проекция А4В4 представляет собой натуральную величину отрезка [АВ]. Таким образом, решение рассмотренной задачи преобразования комплексного чертежа представляет собой еще один способ нахождения натуральной величины отрезка прямой общего положения.
Задача №2.
Перевести плоскость общего положения, заданную треугольником АВС, в проецирующую.
Решение. Плоскость, заданная любым способом, представима как множество соответствующих прямых уровня – либо ее горизонталей, либо фронталей. Поэтому преобразования нужно проводить так, чтобы прямых уровня плоскости спроецировались в точки. Тогда плоскость спроецируется в совокупность точек, расположенных на одной прямой. Следовательно, если в заданной плоскости общего положения провести прямые какого-либо уровня, то, расположив новую плоскость проекций перпендикулярно горизонтальной проекции горизонтали или фронтальной проекции фронтали плоскости, можно получить соответствующую проецирующую плоскость.
Такой подход позволяет находить расстояния от точки до прямой, между плоскостью и параллельной ей прямой, между параллельными плоскостями.
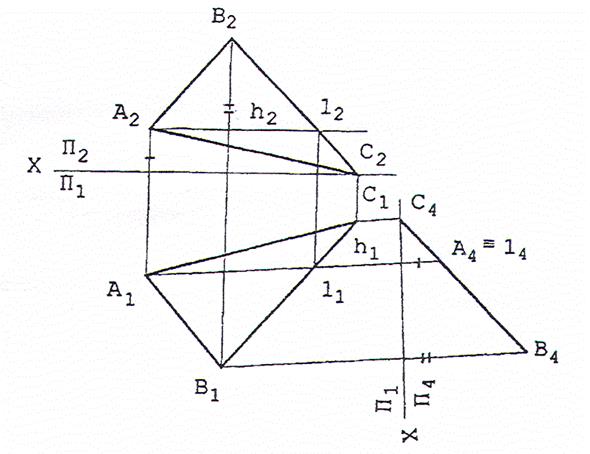
Задача №3.
Плоскость общего положения, заданную треугольником АВС преобразовать в плоскость уровня.
Решение. Задача решается с помощью двух преобразований. Первым (решение исходной задачи 2, изложенной выше), а вторым полученная проецирующая плоскость переводится в положение плоскости уровни. Точки А5, В5 и С5 расположены от оси Х, разделяющей плоскости П4 и П5, на расстояниях, равных величинам координат Y для точек А, В и С в системе плоскостей проекций П1-П4.
Решение рассмотренной задачи позволяет находить натуральные величины плоских фигур (следовательно, сторон многоугольников и плоских углов).
Задача №4.
Построить наклонное сечение пирамиды проецирующей плоскостью (натуральную величину сечения).
Пирамида – непроецирующая поверхность, плоскость является фронтально-проецирующей. Отсюда следует, что одна проекция линии пересечения имеется и совпадает с фронтально-проецирующей плоскостью. Вторую проекцию линии пересечения строим по принадлежности к первой. Соединив проекции точек 1, 2, 3, 4, 5, на П1 получим горизонтальную проекцию линии пересечения.
Для определения натуральной величины сечения введем новую плоскость П4 параллельно фронтально-проецирующей плоскости.
Ось Х1, 2 проведем через проекцию точки 11; ось Х2, 4 – параллельно секущей плоскости на фронтальной плоскости проекций. Проведем линии связи перпендикулярно оси Х2, 4 и перенесем проекцию линии пересечения с П1 на П4. Соединив проекции этих точек на П4, получим натуральную величину сечения.
Индивидуальное задание №1.
Построить натуральную величину сечения конуса фронталью проецирующей плоскостью.
Отчет по практическому занятию.
В ходе выполнения практического занятия изучены методы преобразований чертеже; определение натуральной величины сечения.
Практическое занятие № 6.
(модуль «Поверхности и аксонометрические проекции»)
Тема: Развертывание поверхностей.
Цель занятия: Изучить особенности построения разверток различных поверхностей.
Продолжительность занятия: 10 часов
Вопросы для подготовки к занятию:
1).Какие поверхности называются развертываемыми?
2).Какая плоская фигура получается при развертке боковой поверхности прямого круглого цилиндра?
3). Какие линии получаются при пересечении гранных поверхностей?
Задача №1.
Построить развертку усеченной части.
Чтобы построить развертку боковой поверхности пирамиды необходимо построить три грани в натуральную величину.
Так основание пирамиды является плоскостью уровня, то мы не ищем натуральную величину основания. Поэтому остается определить натуральные величины ребер пирамиды. Определяем натуральные величины ребер способом замены плоскостей проекций. На натуральных величинах ребер определяем также положение точек А, В, С, D, E, F. Сначала строим полную натуральную величину граней и боковой поверхности пирамиды, а затем на ней находим по положению точек линию сечения. К боковой поверхности усеченной части пристраиваем основание, а затем истинный вид сечения, который определили способом замены.
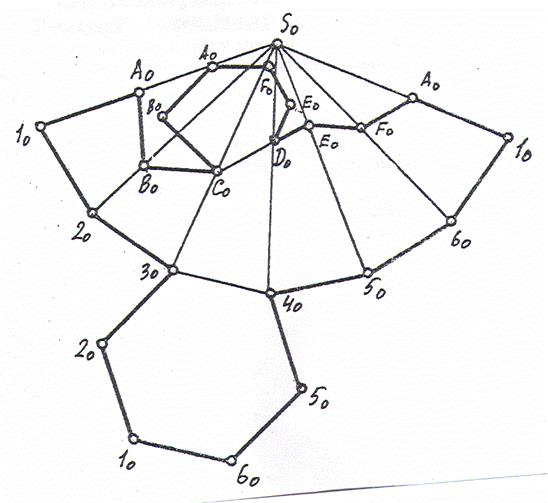
Аналогично строится развертка конуса.
Построение разверток
Развертка поверхности – фигура, получающаяся после одностороннего совмещения поверхности с плоскостью. Каждой точке поверхности соответствует единственная точка на развертке.
Развертывание конической и цилиндрической поверхностей в общем случае производится по схеме развертывания соответственно пирамиды и призмы. Разверткой боковой поверхности прямой призмы и прямого кругового цилиндра является прямоугольник, одна сторона которого есть высота, а другая длина ломаной линии основания призмы или окружности основания цилиндра, которую можно заменить вписанным многоугольником.
Развертка пирамидальных и конических поверхностей строят способом триангуляции. Построение разверток этих сводится к многократному построению натуральных величин треугольников, из которых состоит развертываемая поверхность пирамиды или конуса, который заменяется поверхностью вписанной многогранной пирамидой. «Разрезать» боковую поверхность следует по образующей или по ребру, на которых находится наинизшая точка сечения.
