| 17 |
Решите систему неравенств 
Решение.
Решим первое неравенство системы:
; 
,
откуда 
или 
.
Решим второе неравенство системы:
; 
.
Значит, решения системы неравенств это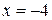 
и .
Ответ: 
; 
.
| Баллы | Критерии оценки выполнения задания |
| Правильно выполнены преобразования, получен верный ответ | |
| Решение доведено до конца, но допущена ошибка вычислительного характера или описка, с её учётом дальнейшие шаги выполнены верно | |
| Другие случаи, не соответствующие указанным выше критериям | |
| Максимальный балл |
| 18 |
Расстояние между городами А и В равно 140 км. Из города А в город В выехал автомобиль, а через 20 минут следом за ним со скоростью 75 км/ч выехал мотоциклист. Мотоциклист догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из С в А, автомобиль прибыл в В. Найдите расстояние от А до С.
Решение.
Пусть искомое расстояние равно 
км, а скорость автомобиля равна 
км/ч. Получаем систему уравнений
откуда 
. Получаем
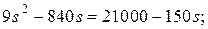
Таким образом, 
или 
. Условию задачи удовлетворяет только (км).
Ответ: 100 км.
| Баллы | Критерии оценки выполнения задания |
| Правильно составлена система уравнений, получен верный ответ | |
| Правильно составлена система уравнений, но при его решении допущена вычислительная ошибка, с её учётом решение доведено до ответа | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
| 19 |
Постройте график функции 
и определите, при каких значениях 
прямая 
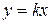имеет с графиком ровно одну общую точку.
Решение.
При 
функция принимает вид:
,
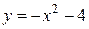её график — парабола, из которой выколота точка 
.
Прямая 
имеет с графиком ровно одну общую точку либо тогда, когда касается параболы, либо тогда, когда пересекает параболу в двух точках, одна из которых — выколотая. Прямая 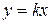касается параболы тогда и только тогда, когда уравнение 
имеет единственный корень, то есть при 
, 
.
Поэтому 
, или .
Ответ: , или .
| Баллы | Критерии оценивания выполнения задания |
| График построен правильно, верно указаны все значения , при которых прямая имеет с графиком только одну общую точку
| |
| График построен правильно, указаны не все верные значения
| |
| Другие случаи, не соответствующие указанным выше критериям | |
| Максимальный балл |
| 20 |
Окружность, проходящая через вершины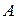 
и 
треугольника 
, пересекает стороны 
и 
в точках 
и 
соответственно, отличных от 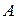и . Докажите, что треугольники и 
подобны.
Доказательство.
Четырёхугольник 
вписан в окружность, поэтому
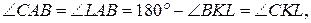
Значит, треугольники и подобны по трём углам.
| Баллы | Критерии оценки выполнения задания |
| Доказательство верное, все шаги обоснованы | |
| Доказательство в целом верное, но содержит неточности | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
| 21 |
Углы при одном из оснований трапеции равны 
и 
, а отрезки, соединяющие середины противоположных сторон, равны 21 и 12. Найдите основания трапеции.
Решение.
Пусть 
— трапеция с основаниями 
и , 
. Обозначим точку пересечения прямых 
и 
через 
, а середины оснований и через 
и 
соответственно. Тогда 
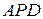. Треугольники 
и 
прямоугольные, поэтому
то есть точки , и лежат на одной прямой. Значит,
Кроме того, средняя линия трапеции равна 
. Значит,
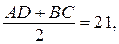
откуда 
, 
.
Ответ: 9 и 33.
| Баллы | Критерии оценки выполнения задания |
| Ход решения верный, все его шаги выполнены правильно, получен верный ответ | |
| Ход решения верный, чертёж соответствует условию задачи, но пропущены существенные объяснения или допущена вычислительная ошибка | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
| 22 |
Спортсмен стреляет по пяти мишеням. Вероятность попадания в мишень при одном выстреле равна 
. На каждую мишень спортсмен имеет две попытки.
а) Найдите вероятность того, что спортсмен попадёт в первую мишень.
б) Найдите вероятность того, что спортсмен попадёт ровно в четыре мишени.
Решение.
а) Спортсмен не попадёт в первую мишень, если обе его попытки будут неудачными. Вероятность этого равна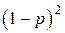 
. Значит, вероятность того, что он попадёт в первую мишень, равна 
.
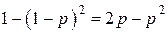б) Вероятность попадания в каждую мишеней равна 
. Число способов выбрать четыре мишени из пяти равно 5. Значит, искомая вероятность равна 
.
Ответ: а) ; б) .
| Баллы | Критерии оценки выполнения задания |
| Обоснованно получены верные ответы в пунктах а) и б) | |
| Обоснованно получен верный ответ в пункте а) или б) | |
| Другие случаи, не соответствующие указанным выше критериям | |
| Максимальный балл |
[1] Каждое задание может относиться более чем к одному разделу кодификатора требований.
