НАПРАВЛЕНИЕ ПОДГОТОВКИ
СТРОИТЕЛЬСТВО
Дисциплина МАТЕМАТИКА
I семестр – 4 з.е.
- лекции – 32 часа (2 часа в неделю);
- практические занятия – 32 часа (2 часа в неделю);
- экзамен
Модуль 1
«Аналитическая геометрия
с элементами линейной алгебры»(2з.е..)
- векторы;
- аналитическая геометрия на плоскости и в пространстве;
- матрицы и определители;
- системы линейных алгебраических уравнений;
- решение систем линейных уравнений методом итераций;
Модуль 2
«Математический анализ»(2з.е.)
- элементы теории множеств, мера плоских множеств, отображения множеств, алгебраические структуры;
- функции, основные понятия и определения;
- предел и непрерывность функции одной переменной;
- дифференциальное исчисление функции одной переменной;
- применение дифференциального исчисления к исследованию функций и построению графиков функций;
- приближенное нахождение корней алгебраических уравнений методом Ньютона и методом простых итераций;
- комплексные числа;
| Содержание лекции | 
| |
| 21.11 | Производная функции. 1. Приращение функции и аргумента. Определение производной. 2. Физический смысл производной. Примеры. 3. Основные правила дифференцирования (производная суммы, произведения, частного). 4. Таблица производных элементарных функций (вывод формул по определению). 5. Производная сложной функции. 6. Производные обратных и неявно заданных функций. Логарифмическая производная. 7. Производная функции, заданной параметрически. 8. Геометрический смысл производной. Касательная и нормаль к графику функции. 9. Дифференциал. Геометрический смысл дифференциала. | [1] [2] [3] [4] [5] [6] |
| 28.11 | Теоремы о дифференцируемых функциях. 1. Повторное дифференцирование. Производные высших порядков. 2. Теорема Ферма. 3. Теорема Ролля. 4. Теорема Лагранжа и ее следствия. 5. Теорема Коши. 6. Правило Лопиталя. Раскрытие неопределенностей по правилу Лопиталя. | [1] [2] [3] [4] [5] [6] |
| 5.12 | Применение производной к исследованию функций. 1. Монотонность функции. Признаки монотонности функции. 2. Наибольшее и наименьшее значение функции. 3. Экстремум функции. Необходимое условие экстремума дифференцируемой функции. Достаточные условия экстремума. 4. Выпуклость графика функции. Достаточное условие выпуклости. 5. Точки перегиба. Необходимое условие точки перегиба. 6. Асимптоты. | [1] [2] [3] [4] [5] [6] |
| 12.12 | Общая схема исследования функции. 1. План построения графика функции в декартовой прямоугольной системе координат. 2. Построение графика функции, заданной параметрически. 3. Полярная система координат. Построение графиков в полярной системе координат. Связь декартовой и полярной систем координат. | [1] [3] [9] |
| 19.12 | Комплексные числа. 1.Определение комплексного числа. 2.Алгебраическая форма комплексного числа. 3.Комплексная плоскость. Арифметические действия с комплексными числами. 4.Модуль и аргумент комплексного числа. Тригонометрическая форма комплексного числа. Формулы Муавра. 5.Показательная форма комплексного числа. Формула Эйлера. 6.Нахождение корней алгебраических уравнений. 7.Построение областей на комплексной плоскости. 8.Понятие о функции комплексного переменного. | [1] [3] |
| 26.12 | Численные методы. Приближенное вычисление действительных корней уравнения. 1. Отделение корней уравнения. 2. Метод половинного деления. 3. Метод простых итераций. 4. Метод Ньютона. 5. Комбинированные методы. | [1] [3] [7] [8] |
| Обзор тем первого семестра. |
Рекомендуемая литература.
1. Пискунов Н.С. Дифференциальное и интегральное исчисление. I том. М., «Интеграл-пресс». -2002.
2. Натансон И.П. Краткий курс высшей математики. Учебник для вузов. 2005.
3. Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах. – в двух частях, 2007. М: ОНИКС 21 век. Мир и образование.
4. Шипачев В.С. Основы высшей математики. Учебное пособие для вузов. М: Высш.шк. 2003.
5. Войтюк М.И., Гамалей В.Г. Дифференциальное исчисление функции одной переменной. Методическое пособие, 2011.
6. Кулик А.В., Плотникова Т.Г. Дифференцирование. Практикум. ДВГУПС, 2008.
7. Ушакова Г.А. Метод хорд и касательных. Методические указания, ДВГУПС, 2007.
8. Виноградова П.В., Ереклинцев А.Г. Численные методы: Учебное пособие, ДВГУПС, 2011.
9. Костина Г.В., Марченко Л.В. Исследование функций и построение графиков, 2007.ДВГУПС.
Вопросы к экзамену в I семестре
1. Понятие прямоугольной системы координат. Простейшие задачи аналитической геометрии (расстояние между двумя точками, деление отрезка в данном отношении).
2. Различные способы задания прямой на плоскости. (Общее уравнение прямой, уравнение прямой с угловым коэффициентом, прямая в отрезках, уравнение прямой проходящей, через две точки).
3. Взаимное расположение двух прямых на плоскости. (Угол между прямыми, условие параллельности, условие перпендикулярности прямых).
4. Кривые второго порядка. Окружность. Вывод уравнения.
5. Эллипс. Свойства эллипса.
6. Гипербола. Свойства гиперболы, построение гиперболы.
7. Парабола и её свойства.
8. Полярная система координат, связь между полярными и прямоугольными координатами точки.
9. Определители. Свойства определителей. (Доказать одно свойство).
10. Понятие минора и алгебраического дополнения.
11. Определители. Свойства определителей. Разложение определителя по элементам какой-либо строки или столбца.
12. Решение систем линейных уравнений. Метод Крамера.
13. Матрицы. Основные понятия. Линейные операции над матрицами.
14. Умножение матриц. Свойства умножения матриц.
15. Обратная матрица. Решение систем линейных уравнений матричных методам.
16. Ранг матрицы. Определение. Нахождение ранга методом окаймления миноров.
17. Элементарные преобразования матриц. Нахождение ранга матрицы.
18. Решения систем линейных уравнений. Метод Гаусса.
19. Векторы. Основные понятия.
20. Линейные операции над векторами.
21. Скалярное произведение векторов и его свойства.
22. Векторное произведение двух векторов и его свойства.
23. Смешанное произведение трёх векторов и его свойства.
24. Геометрические приложения скалярного, векторного и смешанного произведений.
25. Плоскость. Способы задания. Взаимное расположение плоскостей.
26. Прямая в пространстве. Способы задания, взаимное расположение двух прямых.
27. Взаимное расположение прямой и плоскости.
28. Основные понятия теории множеств (понятие множества, операции над множествами).
29. Функция. Определение. Способы задания. Чётность, нечетность, периодичность функций.
30. Основные элементарные функции. Их свойства.
31. Понятие последовательности, предел последовательности.
32. Предел функции. Односторонние пределы.
33. Основные теоремы о пределах.
34. Бесконечно малые и бесконечно большие величины их свойства и связь.
35. Свойства предела функции.
36. Непрерывность функции. Свойства непрерывных функций. Классификация точек разрыва.
37. Первый замечательный предел. Доказательство. Второй замечательной.
38. Сравнение бесконечно малых величин и их применение к вычислению пределов. 
39. Определение производной. Геометрический смысл производной.
40. Производная функции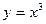 
. Вывод.
41. Производные функций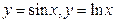 
Вывод.
42. Производные функций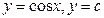 
Вывод.
43. Основные правила, дифференцирования.
44. Производная сложной функции. Теорема.
45. Дифференцирование неявно заданных функций. Правило, привести пример.
46. Понятие обратной функции. Производная обратной функции.
47. Параметрическое задание функций. Производная функции, заданной параметрически.
48. Производные высших порядков.
49. Логарифмическая производная функции.
50. Правило Лопиталя.
51. Возрастание и убывание функции, определения.
52. Экстремум функции. Определения. Необходимые условия существования экстремума.
53. Достаточные условия существования экстремума (с помощью первой и второй производной).
54. Выпуклость и вогнутость функции. Точки перегиба.
55. Асимптоты. Необходимые и достаточные условия существования асимптот графика функции.
56. Численные методы.
57. Комплексные числа. Действия над комплексными числами в алгебраической и тригонометрической формах.
Примеры заданий базового уровня по разделам дисциплины.
Раздел 1. Аналитическая геометрия с элементами линейной алгебры.
1). Определить, при каком значении параметра k прямая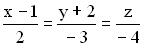 
и плоскость 
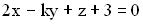параллельны.
2). Перемножить матрицы 
.
3). Найти модуль вектора 
, если А(1,2,5), В(-4,3,1).
4). Вычислить определитель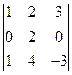 
, разложив его по элементам первой строки.
5). Записать уравнение окружности радиуса 2 с центром в точке М(1;4).
6). Решить систему линейных уравнений
2x – 3y + z = 0
x + y – 4z = 1
y + 2z = 3
7). Построить плоскость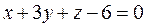 
.
8). Найти скалярное произведение векторов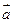 
{1,5,3} и 
{5,1,-7}.
9) Записать уравнение плоскости, проходящей через точку А(4,5,0) перпендикулярно вектору 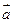{1,-4,8}.
10). Найти векторное произведение векторов 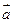{2,1,4} и {0,5,7}.
11). Определить вид кривой и построить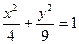 
12) Записать каноническое уравнение прямой, проходящей через точки
А(-1,2,5) и В(7,8,0).
13). Найти смешанное произведение векторов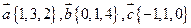 
Раздел 2. Основы математического анализа.
1). Определить точки разрыва функции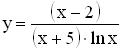 
.
2) Вычислить производную функции 
.
3). Вычислить предел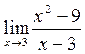 
.
4). Выполнить действия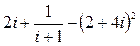 
.
5). Найти область определения функции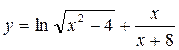 
.
6). Проверить, является ли функция четной или нечетной.
