Взаимное расположение линии второго порядка и прямой на плоскости

Суть метода координат на плоскости. Понятие алгебраической линии. Линии второго порядка. Примеры. Исследование взаимного расположения линии второго порядка и прямой на плоскости. Асимптоты. Касательные. Диаметры линий второго порядка.

 

 

Суть метода Декарта состоит установлении теснейшей связи между геометрическими объектами и алгебраическими формулами. Эта взаимосвязь устанавливается при помощи системы координат. Если на плоскости дана система координат, то для каждой точки можно определить пару чисел, ее координаты, и, обратно, если дана пара чисел, причем указан порядок их соответствия осям координат, то по ним всегда можно построить на плоскости единственную точку.

Из аналитической геометрии известен и другой способ задания линии на плоскости уравнением F(xy)=0. Ограничимся случаем плоскости, укажем лишь как строится понятие алгебраической линии (кривой) - линии, определенной уравнением F(xy)=0, где - целая алгебраическая функция, т.е. многочлен какой-либо степени n. Степень определяет порядок алгебраической линии.

Линии второго порядка, плоские линии, декартовы прямоугольные координаты которых удовлетворяют алгебраическому уравнению 2-й степени

a₁₁x² + a₁₂xy + a₂₂y² + 2a₁₃x + 2a₂₃y + a₁₁ = 0. (*)

Уравнение (*) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую Л. в. п. В зависимости от значений коэффициентов общего уравнения (*) оно может быть преобразовано с помощью параллельного переноса начала и поворота системы координат на некоторый угол к одному из 9 приведённых ниже канонических видов, каждому из которых соответствует определённый класс линий. Именно,

нераспадающиеся линии:

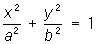— эллипсы,

— гиперболы,

y² = 2px — параболы,

— мнимые эллипсы;

распадающиеся линии:

— пары пересекающихся прямых,

— пары мнимых пересекающихся прямых,

x² - а² = 0 — пары параллельных прямых,

x² + а² = 0 — пары мнимых параллельных прямых,

x² = 0 — пары совпадающих параллельных прямых.

 

Асимптота (от греч. слов: α, συν, πίπτω) - несовпадающая. Под асимптотой подразумевается такая линия, которая, будучи неопределенно продолжена, приближается к данной кривой линии или к некоторой ее части так, что расстояние между обеими линиями делается менее всякой данной величины; иначе говоря, А. касается данной кривой линии на бесконечном расстоянии от начала координат. Всякая другая линия, параллельная А., хотя и приближается непрестанно к кривой, однако, не может быть названа в свою очередь А., так как расстояние ее от кривой не может быть уменьшено по произволению.

Основываясь на вышеприведенном определении, что прямолинейная А. есть касательная к кривой в точке, бесконечно удаленной от начала координат, легко найти уравнение А. данной кривой. В самом деле, пусть y = f(x) есть уравнение кривой линии; уравнение касательной ее в точке, определенной координатами х и у, будет, как известно, У— у = dy/dx(Х — х) или Y = (dy/dx)Х + у — x(dy/dx). Чтобы перейти от касательной к А., стоит сделать одно из следующих предположений: 1) x и y = ±∞, 2) х = ±∞, а у = конечному числу и 3) у = +∞, а х = конечному числу, так как этими предположениями мы выражаем, что точка касания находится на бесконечном расстоянии от начала координат. Так, для гиперболы, определяемой уравнением (x²/a²) — (y²/b²) = 1 находим Y = ±(b/a)∙[x/√(x² — a²)]∙X ± [ab/√(x² — a²)]. Полагая х = ∞, найдем ±(b/a) — [x//√(x² — a²)] = ±(b/a)∙[1/√(1 — a²/ x²)] = ±(b/a), и ±[ab//√(x² — a²)] = 0; следовательно, уравнение А. рассматриваемой гиперболы будет У = ±(b/a)Х или, что все равно, Y = +(b/a)X и Y = -(b/a)X; последние два уравнения показывают, что гипербола имеет две А. Можно также определить А. следующим образом. Пусть будет У А. = Х + В уравнение А., не параллельной оси у. Ордината у кривой, соответствующая абсциссе x, для весьма больших величин сей абсциссы будет очень мало разниться от ординаты У а-ты, так что можно ее принять у = Ах + В ± ε, подразумевая под ε количество, уничтожающееся вместе с 1/x. Итак, полагая x = ∞, найдем пред. (Y/X) = пред.

и пред. (у — Ах) = пред. (В ± ε) = В. Следовательно, для определения постоянного количества стоит только в уравнении кривой положить Y/X = q или y = xq и сыскать предел, к которому стремится q для бесконечно больших значений х. Величина В определится, если в уравнении кривой примем у — Ах = ν, или у = Ах + ν. Изменив х на у и наоборот и рассуждая так же, как и выше, найдем А., не параллельные оси х. Так, например, уравнение рассмотренной нами гиперболы через подстановку qx вместо у дает a²/x² — q²x²/b² = 1 или q² = b²/a² — b²/x²; полагая х = ∞, найдем q² = b²/a², или q = ±(b/a)A. Полагая в том же уравнении y = Ax + ν = +(b/a)x + ν, получим x²/a² — [(±x(b/a) + ν)²/b²] = 1, или ν = ±(b/a)∙[√(x²— a²) — x], где, полагая x = ∞, получим ν = 0 = B; следовательно, уравнение А. предложенной гиперболы будет, как и выше, Y = +(b/a)X, что и требовалось доказать. Бесчисленное множество кривых имеет А.; укажем, кроме упомянутой уже гиперболы, следующие кривые, имеющие А.: конхоида, логарифмическая линия, циссоида, декартов лист и др.

В курсе аналитической геометрии доказывается, что середины параллельных хорд линии второго порядка лежат на одной прямой. Эта прямая называется диаметром линии второго порядка. Диаметр, делящий пополам какую-нибудь хорду (а значит, и все параллельные ей), называется сопряженным этой хорде (и всем хордам, который ей параллельны). Все диаметры эллипса и гиперболы проходят через центр. Если эллипс задан уравнением

(1)

то его диаметр, сопряженный хордам с угловым коэффициентом k, определяется уравнением

.

Если гипербола задана уравнением

, (2)

то ее диаметр, сопряженный хордам с угловым коэффициентом k, определяется уравнением

.

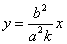Все диаметры параболы параллельны ее оси. Если парабола задана уравнением

,

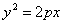то ее диаметр, сопряженный хордам с угловым коэффициентом k, определяется уравнением

.

Если один из двух диаметров эллипса или гиперболы делит пополам хорды, параллельные другому, то второй диаметр делит пополам хорды, параллельные первому. Такие два диаметра называются взаимно сопряженными.

Если k и k’ - угловые коэффициенты двух взаимно сопряженных диаметров эллипса (1), то

(3)

Если k и k’ - угловые коэффициенты дух взаимно сопряженных диаметров гиперболы (2), то

(4).

Соотношения (3) и (4) называются условиями сопряженности диаметров соответственно для эллипса и для гиперболы.

Диаметр линии второго порядка, перпендикулярный к сопряженным хордам, называется главным.

 

3) Основные задачи на прямую и плоскость в пространстве.

Перечислить основные задачи на прямую и плоскость в пространстве. Обосновать их решение в общем виде, привести примеры.

1. Рассмотрим в общем виде несколько задач на прямую, кото­рые часто приходится решать методом координат (система коор­динат аффинная).

Задача 1. Написать уравнение прямой d, проходящей че­рез точку mo (jco, yo) и параллельной прямой, заданной уравне­нием Ах + Ву + С = 0.

Решение. По теореме (по Линия на плоскости, заданная в аффинной системе координат уравнением первой степени Ax + By + C = 0, (1) есть прямая. Вектор (—В, А) является направляющим вектором этой прямой.) вектор 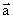(-В, А) является направляющим вектором данной прямой, поэтому он является также направляющим вектором прямой d. Таким образом, прямая d задана направляющим вектором 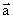(— В, А) и точкой mq (x₀, у₀), следовательно, имеет уравнение 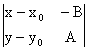= 0, или А(х-х₀)+В(у-y₀) = 0 (1)

Задача 2. Найти координаты точки пересечения непарал­лельных прямых, заданных уравнениями:

А₁х + В₁y + C₁ = 0

А₂х + В₂y + C₂ = 0 (2)

Решение. Для нахождения координат точки пересечения данных прямых следует решить систему (2) относительно х и у.

В данном случае, ≠ 0, поэтому система (2) имеет единст­венное решение:

(3)

Точка (х₀, у₀) является точкой пересечения данных прямых.

Задача 3. Написать уравнение прямой, проходящей через точку М₁ (х₁, у₁) и через точку пересечения двух прямых, задан­ных уравнениями (2).

Решение. Первый способ. По формулам (3) найдем координаты x₀, у₀ точки Мо пересечения прямых (2), а затем за­пишем уравнение прямой, проходящей через точки M₁ и М₀.

Второй способ. Искомое уравнение прямой, проходя­щей через точку пересечения прямых, заданных уравнениями (2), можно записать в виде

λ(A₁x + B₁y + C₁)+μ (A₂x + B₂y + C₂) = 0, (4) где λ и μ — числовые коэффициенты, не равные одновременно нулю. Действительно, уравнением (4), по теореме (по Линия на плоскости, заданная в аффинной системе координат уравнением первой степени Ax + By + C = 0, (1) есть прямая. Вектор (—В, А) является направляющим вектором этой прямой.), зада­ется прямая (легко проверить, что коэффициенты при х и у одновременно не равны нулю), причем при произвольных значе­ниях λ, и μ, не равных одновременно нулю, эта прямая проходит через точку М₀ пересечения прямых (2).

Коэффициенты λ и μ подберем так, чтобы прямая (4) прохо­дила через точку М₁ (х₁, у₁). Для этого λ и μ должны удовлетво­рять условию: λ(A₁x + B₁y + C₁)+μ (A₂x + B₂y + C₂) = 0.

Пример. Написать уравнение прямой d, проходящей через точку M₁ (-2, 6) и через точку пересечения прямых, заданных уравнениями: х — 3y + 1 = 0 и 2x + 4y = 0.

Решение. Задачу решим вторым способом. В данном слу­чае уравнение (4) имеет вид: λ(x - 3y + 1)+μ (2x + 4y) = 0. Пря­мая d проходит через точку M₁ (— 2, 6), поэтому λ(-2 – 18 + 1) + μ (-4 + 24) = 0, или -19x + 20y = 0. Этому равенству удов­летворяют, например, числа λ = 20, μ = 19. Таким образом, ис­комое уравнение имеет вид: 20 (х — 3y + 1) + 19 (2x + 4y) = 0, или 29x + 84y + 10 = 0.

2. Рассмотрим теперь задачи в прямоугольной системе коор­динат.

Задача 4. Написать уравнение прямой d, проходящей че­рез точку М₀ (x₀, у₀) и перпендикулярной вектору (А, В).

Решение. Произвольная точка М (х, у) плоскости принад­лежит прямой d тогда и только тогда, когда вектор пер­пендикулярен вектору . Так как имеет координаты (x — x₀, у — у₀), то условие перпендикулярности векторов и запишется так: А(х - x₀) + В(у - у₀) = 0.

Это и есть уравнение прямой, проходящей через точку M₀(x₀, у₀) и перпендикулярной вектору (А, В).

Задача 5. Написать уравнение прямой d, проходящей че­рез точку M₀ (x₀, у₀) и перпендикулярной прямой l, заданной урав­нением Ax + By + C = 0.

Решение. Вектор (А, В) перпендикулярен прямой l, поэтому является направляющим вектором прямой d. Таким образом, прямая d определяется точкой M₀ (x₀, у₀) и направляю­щим вектором (А, В), т. е. имеет уравнение или В(х- х₀) - А(у – у₀) = 0.

Задача 6. На плоскости дана прямоугольная система координат Оху. Написать уравнение прямой d, если известно, что она проходит через точку М₀ (х₀, у₀) и угол между прямыми Ох и d равен φ.

Решение. Так как система координат прямоугольная, то угло­вой коэффициент прямой d равен tg φ. Поэтому искомое уравнение прямой d имеет: у – y₀ = tgφ (x – x₀).