Дистанционный урок за 01.01.2012 по геометрии для 9 А,Б №1.
Вы должны знать: определение вектора, его способы обозначения, формулы для вычисления координат вектора и абсолютной величины.
Вы должны уметь: строить вектор в Декартовой системе координат, решать базовые задачи, приведённые после теории.
(Выучить) Вектором называется направленный отрезок.
У отрезка AB его концы равноправны А у вектора – нет! Для вектора один из концов отрезка, например, А называется началом, а другой, то есть В, - концом. Обозначим вектор либо указанием концов отрезка, причем начало вектора ставится на первое место, либо строчной

| 
| 
|
| Рис.12.1.1а. | Рис.12.1.1б. | Рис.12.1.1в. |
латинской буквой со стрелкой или чертой над буквами. На Рис.12.1.1а. изображен обычный отрезок AB, а на Рис.12.1.1б. - вектор  , на Рис.12.1.1в. - вектор
, на Рис.12.1.1в. - вектор  .
.
Векторы  и
и  называются одинаково направленными или сонаправленными, если лучи AB и CD одинаково направлены. Если лучи AB и CD противоположно направлены, векторы
называются одинаково направленными или сонаправленными, если лучи AB и CD одинаково направлены. Если лучи AB и CD противоположно направлены, векторы  и
и  называются противоположно направленными.
называются противоположно направленными.
(Выучить) Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Рис.12.1.2.
(Выучить) Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютную величину вектора  обозначим
обозначим  .
.
(Выучить) Два вектора называются равными, если они одинаково направлены и равны по абсолютной величине.
Углом между ненулевыми векторами  и
и  называется угол (BAC). Углом между любыми двумя ненулевыми векторами
называется угол (BAC). Углом между любыми двумя ненулевыми векторами  и
и  называется угол между равными им векторами с общим началом. Угол между одинаково направленными векторами равен нулю. Нулевым вектором
называется угол между равными им векторами с общим началом. Угол между одинаково направленными векторами равен нулю. Нулевым вектором  называется вектор, у которого начало совпадает с концом. Направление нулевого вектора не определено, а его модуль считается равным нулю. На Рис.12.1.3.вектор
называется вектор, у которого начало совпадает с концом. Направление нулевого вектора не определено, а его модуль считается равным нулю. На Рис.12.1.3.вектор  , а вектор
, а вектор  . Вектор называется единичным, если его абсолютная величина равна единице.
. Вектор называется единичным, если его абсолютная величина равна единице.

| 
|
| Рис.12.1.2. | Рис.12.1.3. |
(Выучить) Координатами вектора  называются числа (a1;a2)
называются числа (a1;a2)
a1 = x2 - x1, a2 = y2 - y1.
X1, y1)- координаты начала
X2, y2)- координаты конца
Для обозначения того, что вектор  имеет координаты a1 и a2 используют запись
имеет координаты a1 и a2 используют запись 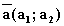 . Абсолютная величина вектора
. Абсолютная величина вектора 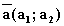 равна
равна  .
.
(Выучить) Т12.4 Если два вектора равны, то равны и их соответствующие координаты.
(Выучить) Т12.5. Если у двух векторов соответствующие координаты равны, то эти вектора равны.
Задачи решаем в рабочей тетради
 Начальный и средний уровни (6б.)
Начальный и средний уровни (6б.)
№1. АВСD – параллелограмм.
1) Запишите все векторы, изображённые на рисунке,
Например:  , …,…,…, ….
, …,…,…, ….
2) запишите сонаправленные векторы.
3) запишите противоположно направленные векторы.
4) запишите пары коллинеарных векторов.
5) какой из векторов не имеет пары – коллинеарного вектора.
6) Какие векторы будут равными?
7) Найдите абсолютную величину вектора  , если
, если  см, а угол А равен 600.
см, а угол А равен 600.
Достаточный уровень (3б.)
№2. Дано точки А(3;1), В(5;3). Найти
1) координаты векторов  и
и  , сделайте вывод, одинаковы ли эти координаты?
, сделайте вывод, одинаковы ли эти координаты?
2) Постройте вектора в разных системах координат, сделайте вывод,
- коллинеарные ли они,
- равны ли,
- сонаправлены или прот. направоены?
- Можно ли по координатам вектора построить сам вектор, или нужны координаты начала и конца?
3) Найдите абсолютные величины этих векторов.
Высокий уровень (но не сложно!) (3б.)
№3. Вектор  имеет координаты (3;m). Его абсолютная величина 5. Найти m.
имеет координаты (3;m). Его абсолютная величина 5. Найти m.
Учитель Новикова Виктория Леонидовна




