Практические задания.
Индивидуальные условия заданий приведены в таблицах раздела 1 и определяются по номеру варианта n, а также с помощью параметров:
α1=-1-n (mod 7); α2=n (mod 5); α3 =-3-n (mod 3), где p (mod q) - остаток от деления p на q.
Задание 1.
На плоскости даны точки А(α1; α2-2) и В(α2-2;α2+4)
Найти:
а) точку C(x1;y1)-середину отрезка AB;
б) точку D(x2;y2), которая делит отрезок АВ в отношении p:q.
Параметры p,q приведены в табл. 1.1.
Таблица 1.1.
ПАРАМЕТРЫ p,q К ЗАДАНИЮ 1.
| n(mod 10) | p | q | n(mod 10) | p | q |
Задание 2.
На плоскости даны точки А (x1;y1), В (x2;y2) и С (x3;y3). Сделайте чертеж треугольника АВС и найдите:
а) длину и уравнение стороны ВС (записать общее уравнение,
каноническое, параметрическое и с угловым коэффициентом);
б) косинус угла А и угол А (в градусах);
в) уравнение пряной, проходящей через точку А параллельно
стороне ВС;
г) высоту, проведенную к стороне ВС,и ее уравнение;
д) уравнение медианы, проведенной к стороне ВС;
е) уравнение биссектрисы угла А;
ж) координаты центра и радиус вписанной окружности;
з) координаты центра и радиус описанной окружности:
и) площадь треугольника;
к) координаты центра (тяжести) треугольника.
Таблица 1.2.
КООРДИНАТЫ ТОЧЕК А, В, С К ЗАДАНИЮ 2.
| N | x1 | y1 | x2 | y2 | x3 | y3 |
| -1 -7 -1 -5 -1 -5 -2 -3 -3 -9 -7 -2 -1 -7 -6 -5 -5 -1 -3 -7 -1 -3 -7 -5 -2 -4 -3 -2 -6 -1 -5 -3 -3 -4 -1 -1 -2 -3 -8 -3 -11 -14 -1 -6 -9 -7 -7 -3 -7 -3 -3 -8 -7 -13 -3 -2 | -1 -2 -1 -2 -6 -6 -11 -7 -4 -9 -1 -3 -6 -1 -1 -3 -8 -4 -1 -1 -9 -3 -8 -5 -2 -6 -9 -2 -6 -3 -2 -3 -6 -3 -1 -7 -1 -5 -1 -5 -2 | -1 -3 -1 -5 -5 -9 -7 -2 -7 -14 -7 -1 -9 -8 -4 -7 -8 -7 -1 -7 -2 -6 -2 -5 -11 -11 -3 -7 -1 -3 -7 -3 -7 -5 -4 -3 -6 -6 -3 -3 -3 -5 -5 -5 -1 -1 -1 | -1 -2 -2 -2 -6 -4 -2 -1 -4 -6 -9 -7 -1 -1 -1 -1 -3 -1 -3 -6 -2 -1 -3 -7 -6 -1 -6 -10 -5 -6 -1 -6 -9 -8 -3 -8 -1 -1 -7 -5 -11 -1 -4 -1 -1 -4 -1 -4 -3 | -5 -5 -4 -3 -7 -3 -7 -1 -11 -14 -9 -2 -8 -6 -1 -3 -3 -3 -4 -1 -7 -1 -7 -5 -14 -1 -3 -11 -3 -2 -5 -8 -6 -7 -3 -1 -2 -11 -1 -5 -7 -7 -3 | -1 -2 -1 -3 -3 -5 -1 -4 -8 -2 -3 -7 -1 -3 -1 -6 -3 -5 -9 -2 -11 -7 -7 -1 -1 -18 -4 -5 -6 -1 -9 -3 -6 -1 -4 -2 -2 |
Задание 3.
Решите планиметрическую задачу (см. табл.1.3.).
Таблица 1.3.
ЗАДАЧИ К ЗАДАНИЮ 3.
| n | Условие задачи. |
| На прямой 2x + y + 11=0 найти точку, равноудаленную от двух точек А (1;1),В (3;0) | |
| Найти координаты точки, симметричной точке (2;-4) относительно прямой 4x + 3y + 1=0 | |
| Найти уравнение диагонали параллелограмма, проходящей через точку пересечения его сторон x + y - 1=0 или y + 1=0, если известно, что диагонали параллелограмма пересекаются в точке В (-1;0) | |
| Составить уравнение прямой, проходящей через точку А(2;6) и образующей с осями координат треугольник, который находится во второй четверти и имеет площадь 3 кв.ед. | |
| Составить уравнение прямой, проходящей черев точку А(-1;2) так, что середина ее отрезка заключенного между параллельными прямыми х + 2y + 1=0 и x + 2у - 3 = 0, лежит на прямой х - у - 6 =0 | |
| Даны уравнения двух сторон треугольника 4х-5у+ 9=0 и х + 4у -3=0. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке (3;1) | |
| Вычислить координаты вершин ромба, если известны уравнения двух его сторон 2х - у+4=0 и 2х – у + 10=0 и уравнение одной из него диагоналей х + у + 2=0 | |
| Составить уравнения сторон треугольника, если А(-5;5), В(3;1) - две его вершины, а D(2;5) - точка пересечения его высот | |
| Дано уравнение одной из сторон квадрата х + 3у – 7=0 и точка пересечения его диагоналей Р(0;-1). Найти уравнения трех остальных сторон этого квадрата | |
| Даны уравнения одной ид сторон ромба х - 3у + 10 =0 и одной из его диагоналей х + 4у - 4=0. Диагонали ромба пересекаются в точке Р(0; 1). Найти уравнения трех остальных сторон ромба | |
| Уравнения двух сторон параллелограмма х + 2у + 2=0 и х + у – 4=0, а уравнение одной из диагоналей x – 2=0. Найти координаты вершин | |
| Даны вершины А(-3;-2) и В(8;-4) трапеция АВСD (АГ || ВС). Известно, что диагонали трапеция равны и точка пересечения диагоналей. О(0;2). Найти координат вершин С и 1) этой трапеции | |
| Даны вершины А(2;-2) и В(-1) и точка Р(1;0) пересечения медиан треугольника. Составить уравнение высоты треугольника, проведенной через третью вершину С | |
| Даны уравнения двух высот треугольника 3х + 2у- 34=0 и х + у – 1=0 и одна из вершин А(6; 5). Составить уравнения сторон | |
| Даны уравнения двух медиан 2х -11y+ 28=0 и 5х + 7у – 22=0 и одна из вершин (-2;-2) треугольника. Составить уравнения сторон | |
| Две стороны треугольника заданы уравнениями 2х+ + у - 1 =0 и х - 3у +14=0, а середина третьей стороны совпадает с началом координат. Составить уравнение третьей стороны | |
| Даны уравнения сторон треугольника: (АВ) 7х - 2у + 32=0;(АС) x + у + 2 =0; (ВС) 4х + у - 1=0. Найти точку пересечения его высот | |
| Составьте уравнения катетов прямоугольного равностороннего треугольника, если уравнение гипотенузы 3х - у + 11=0 и С (4;3) - вершина прямого угла | |
| В равнобедренном треугольнике известны: уравнение основания 5х 4 - 63 =0, уравнение одной из боковых сторон х + 4у – 14=0 и точка на второй боковой стороне (3;7). Найдите уравнение второй боковой стороны | |
| Одна и сторон квадрата лежит на прямой х -5y+32=0, а одна из вершине находится в точке (2;1). Найдите уравнения остальных сторон квадрата | |
| Составить уравнения трех сторон квадрата, если известно, что четвертой стороной является отрезок прямой 4х - 7у + 28=0, концы которого лежат на осях координат | |
| Точки К (1;3) и L (-1;1) являются серединами оснований равнобедренной трапеции, а точки Р (3;0) и Q (-3;5) лежат на ее боковых сторонах. Составить уравнения сторон трапеции | |
| Даны стороны треугольника: (АС) 2х - 15у – 55= 0; (АВ) 4x- 3у + 25=0; (BC) 14х + 3у- 61 - 0. Составить уравнение прямой, проходящей через вершину С и черев точку на стороне АВ, делящую ее (считая от вершины А) в отношении 1:4 | |
| Точки В (7;1) и D (9;-3) являются противоположнымивершинами квадрата. Определить координаты двух других вершин | |
| В треугольнике известны уравнения высоты х + у- 3=0 и медианы х - 4у + 10=0, проведенных из различных вершин. Написать уравнения сторон треугольника, зная одну его вершину (8;9) | |
| Написать уравнение сторон треугольника, зная одну его вершину (6;3), уравнения высоты х - 9у + 75=0 и биссектрисы х - 13у +79=0, проведенных из одной вершины | |
| Точка А (2;0) является вершиной правильного треугольника, а противолежащая ей сторона лежит на прямой х + у -1=0. Составить уравнения двух других сторон | |
| Длина стороны ромба с острым углом 60° равна 2. Диагонали ромба пересекаются в точке М (1;2), причем большая диагональ параллельна оси абсцисс. Составить уравнения сторон ромба | |
| Точка А (1;2) является серединой одного из оснований прямоугольной трапеции, а точка В (3;-1) - серединой средней линии. Боковая сторона, перпендикулярная основаниям, лежит на прямой 4х - 3у + 10=0. Составить уравнения остальных сторон трапеции | |
| Написать уравнения сторон треугольника, зная одну его вершину (9;2), уравнения биссектрисы х + у- 5=0 и медианы х - у =0, проведенных из различных вершин | |
| Даны координаты двух вершин треугольника А (-1;3), В (2;5) и ортоцентр - точка Н (1;4). Найти координаты третьей вершины треугольника. Ортоцентром треугольника называется точка пересечения его высот. | |
| Точка Н (-3;2) является точкой пересечения высот треугольника, две стороны которого лежат на прямых 2х-у=0 и х + у- 3=0. Составить уравнение третьей стороны | |
| Найти радиус и координаты центра окружности, проходящей через точку А (-1;3) и касающейся прямых 7х + у =0 и х - у + 8=0 | |
| Окружность проходит через точки М (1;0) и N (2;1). Найдите центр этой окружности, если известно, что он лежит на прямой 5х - у -4=0 | |
| Точки В (1;2) и С (3;-6) симметричны относительно некоторой прямой. Составить уравнение этой прямой | |
| Диагонали параллелограмма пересекаются в точке К (-2;4). Составить уравнение диагонали, не проходящей через точку пересечения сторон 4х - у + 4=0 и 4х + 3у + 20=0 | |
| Площадь прямоугольного треугольника, катетами которого является оси координат, равна 8. Составить уравнение гипотенузы, если известно, что они проходит через точку А (-4;8) | |
| Составить уравнение прямой L1, параллельной прямойL2:2х + 3у – 23=0, если середина отрезка прямой L3: 5х + 2 + 3=0,заключенного между параллельными прямыми L1 и L2 лежит на прямой L4: 5х - у + 24=0 | |
| Составить уравнение стороны треугольника, в котором известны точка пересечения медиан (-1;7): уравнения двух других сторон x + 4у -37=0, 2х - у +16=0 | |
| Даны две стороны х - у + 5=0 и х – у + 10=0 диагональ 3х + у -10=0 ромба. Найти вершины ромба | |
| В треугольнике известны две вершины А (-2;9), В (2;-3) и точка пересечения высот О (2;7). Написать уравнения сторон | |
| Точка А (3:-2) является вершиной квадрата, а точка М(1;1) - точкой пересечения его диагоналей. Составить уравнения сторон квадрата | |
| Даны уравнения одной ив сторон ромба х + у - 39=0 и одной из его диагоналей х-3у+11=0. Найти уравнения остальных сторон ром ба, если его центр - точка N (-2;3). |
| Найти координаты вершин параллелограмма, в котором известны две стороны 2х - 5у – 5=0 и 2х + 5у – 15=0 и диагональ 6х + 5у – 35=0 | |
| Найти координаты точек С и D четырехугольника АВСD, в котором отрезки АВ и DС параллельны, BD и АС перпендикулярны друг другу и заданы вершины А(9;-1), В (0;5) | |
| Даны две вершины (3;-1), (1;4) и центр тяжести (0-.2) треугольника. Найти координаты третьей вершины треугольника и составить уравнения его сторон | |
| Даны уравнения двух высот треугольника 3х + 4у - 23 =0 и 12х - 5у - 24 =0 и одна из его вершин (1;1). Составить уравнения сторон | |
| Написать уравнения сторон треугольника, две медианы которого лежат на прямых х + у - 3 = 0 и 2х +3у -1=0, а точка А (1;1) является вершиной треугольника | |
| Две стороны треугольника заданы уравнениям: х + 3у - 21=0 и 7х + у + 13 = 0, середина третьей стороны - точка (2;3). Составить уравнение третьей стороны | |
| Даны уравнения сторон треугольник: (NM) 3х - 5у+ +17=0, 8x + 6у – 32=0, (NР) 5х + 11у + 9=0. Найти ортоцентр треугольника. (Ортоцентром треугольника называется точка пересечения его высот) | |
| Гипотенуза прямоугольного треугольника лежит на прямой 2х + у -2=0, а точка С (3;-1) является вершиной прямого угла. Площадь треугольника равна 9/4. Составить уравнения прямых, на которых лежат катеты | |
Основание равнобедренного треугольника лежит на прямой х + 2у-2=0, а одна из боковых сторон - на прямой у + 2х – 1=0. Составить уравнение другой боковой стороны треугольника, зная, что её расстояние от точки пересечения данных прямых равно 
| |
| Составить уравнения сторон квадрата, в котором одна из вершин - точка (8;7) и одна из сторон лежит на прямой 5х + 2у + 4=0 | |
| Составить уравнения трех сторон квадрата, если известно, что четвертой стороной является отрезок прямой 2х + у – 8=0, концы которого лежат на окружности (х -3)2+y2= 4 | |
| Точки М(3;7) и. К (2;3) являются серединами оснований равнобедренной трапеции. Точки К(1;7) и Р(4;6,5) лежат на ее боковых сторонах. Составить уравнения сторон трапеции | |
| Даны стороны треугольника: (АВ) 4х + 3у - 10 =0; (ВС) 8х + 2у - 8 =0; (АС) 8х + 5у – 18=0. Составить уравнение прямой, проходящей через точку С и долящей сторону АВ в отношении 2:3 (считая от вершины А) | |
| Противоположными вершинамиквадрата являются точки (-5;-3) и (3;17). Найти координаты двух других вершин | |
| Написать уравнения сторон треугольника, зная одну его вершину (2;7), уравнение медианы 9х +у + 4=0 и высоты х + 3у – 11=0, проведенных из различных вершин | |
| Написать уравнения сторон треугольника, зная одну его вершину (-5;4), уравнения высоты 6х + у – 61=0 и биссектрисы 4х - 3у + 7=0 | |
| Точка М(6;4)является вершиной правильного треугольника, а противолежащая ей сторона лежащего на прямой 3х – у + 2 = 0. Найти уравнения остальных сторон треугольника. | |
| Длина стороны ромба с тупым углом 120° равна 6/2. Меньшая диагональ параллельна биссектрисе 2 и 4 координатных углов. Диагонали пересекаются в точке (-4:6). Составьте уравнения сторон ромба | |
| Точка Р(8;1) является серединой одного из оснований прямоугольной трапеции, а точка N(2:3) - серединой средней линии. Боковая сторона, перпендикулярная основаниям, лежит на прямой 4х + 3у +1=0. Составить уравнения сторон | |
| Составьте уравнения трех сторон треугольника, в котором медиана 3х + 2у – 6=0 и биссектриса х – у =0 проведены не из вершины (4;0), а из двух других вершин | |
| Даны стороны треугольника: 4х - 3у + 26 =0 (АВ); х + 2у + 1=0 (АС); 7x+ 3у-37=0 (ВС). Найти точку пересечения медианы, проведенной из вершины В и высоты, преходящей через вершину С | |
| Найти радиус и координаты центра окружности, проходящей через точку А(-1;8) и касающейся прямых х + 10=0 и 4х-3у+10=0 | |
| Точка К отстоит на одинаковых расстояниях от точек Р(7;8) и Q (1;2). Найти координаты точки К, если известно, что она лежит на прямой 4х - 5у + 27=0 | |
| Найти координаты точки N симметричной точке М относительно прямой х + у - 5 =0. Точка М отстоит от прямой на расстоянии вдвое большем, чем точка К (-2;7) и находится с ней по одну сторону от прямой, причем отрезок КМ перпендикулярен прямой | |
| В параллелограмме две стороны заданы уравнениями х - 5у + 7=0 и 5х – 3 у - 9=0. Составить уравнение диагонали параллелограмма, не проходящей через точку пересечения этих сторон, если известно, что диагонали пересекаются в точке М(2;4) | |
| Найти координаты вершин треугольника, симметричного треугольнику АВС относительно центра описанной около треугольника АВС окружности, если А(9;-1) В(5;1), С(0;-5) | |
| Составить уравнение прямой, перпендикулярной прямой х + 3у-13=0 и образующей с осями координат треугольник, площадь которого равна 6 |
| Составить уравнение прямой, проходящей через точку А(1;2) так, что отрезок этой прямой, заключенный между прямыми 3х + у + 2=0 и 4х + у – 1=0, в точке А делится пополам | |
Центр тяжести треугольника - точка ( ; ;  ).
Уравнения двух его сторон 4х + у + 14=0 и
- 6y - 9=0. Составить уравнение третьей стороны ).
Уравнения двух его сторон 4х + у + 14=0 и
- 6y - 9=0. Составить уравнение третьей стороны
| |
| Известны уравнения двух сторон ромба 7х - 9y - 39 =0 и 3х + 11y -91=0 и одной из его диагоналей 5х + у - 13=0. Вычислить координаты вершин ромба | |
| Составить уравнение третьей стороны треугольника, если известны уравнения двух его сторон 6х - у - 11=0 и 4х + 5у + 13=0 и ортоцентр- точка (-1;2) | |
| Написать уравнения сторон квадрата, центр которого - точка (1-3), а одна из вершин - точка (-4:7) | |
| Написать уравнения сторон ромба, если известны диагональ х + у – 2=0, точка её пересечения с другой диагональю (0;2) и одна из сторон 3х - у – 10=0 | |
| Вычислить координаты вершин параллелограмма, в котором две стороны лежат на прямых 2х - 5у- 5=0 и 2х + 5у -15=0, а одна из диагоналей на прямой 6х + 6у - 35=0 | |
| Диагонали трапеции ABCD (АD || BC) перпендикулярны друг другу и заданы вершины А (4;-1) и В(iЗ;6). Найти координаты вершин C и D трапеции | |
Составить уравнения сторон треугольника, в котором даны две вершины (-7;6) и (7;4) и точка пересечения отрезков, соединяющих эти вершины с серединами противоположных сторон 
| |
| Даны уравнения двух высот треугольника x - 5у + 16 = 0 и 9x + 7у + 14=0 и одна из ёе вершин (-6:-З). Написать у равнения сторон треугольника | |
| Даты уравнения двух медиан 3x+ 3y+2=0 и 2х + 2у – 21=0 треугольника и одна из вершин М(5;-1). Найти уравнения сторон треугольника | |
| Середина одной из сторон треугольника - точка (0;3).Две другие стороны лежат на прямых х - 9у + 52= 0 и х + у – 8= 0. Составить уравнение третьей стороны | |
| Найти точку пересечения высот треугольника, стороны которого лежат на прямых 6х + у – 23=0, 9х - 4у – 7=0, 3х - 5у – 17=0 | |
| Точка С (6;1) - вершина прямого угла в треугольнике, а гипотенуза лежит на прямой 2х-3у+5=0. Написать уравнения катетов, один из которых лежит на прямой, содержащей точку (-4;-25). |
Точки А (1;2) и В(3;0) - вершины равнобедренного треугольника АВС, углы А и В при основании равны аrссоs  . Найти координаты вершины С, зная, что она лежит по ту же сторону от прямой АВ, что и точка М(2;3) . Найти координаты вершины С, зная, что она лежит по ту же сторону от прямой АВ, что и точка М(2;3)
| |
| Составить уравнения сторон квадрата по известному уравнению одной из сторон х + 8у – 17=0 и одной ив вершин (2;9) | |
| Даны уравнения сторон квадрата 4х + у - 9=0 и 4х + у + 36=0. Составить уравнения двух других его сторон при условии, что точка А (6;2) лежит на стороне этого квадрата | |
Точки М(5;-1) и N(-3;7) являются серединами оснований равнобедренной трапеции, а точки P(-1;-  ) )  и К (4;6) лежат на боковых сторонах. Составить уравнения сторон трапеции и К (4;6) лежат на боковых сторонах. Составить уравнения сторон трапеции
| |
| Даны стороны треугольника 9х - 2у - 51 =0 (АС), 4х + 3у +24 =0 (АВ), x + 2у + 1=0 (ВС). Составить уравнение прямой, проходящей через вершину С и точку К на стороне AB, делящую ее в отношении 3:7 (считая от вершины В) | |
| Точки а(9;8) и D (-1;4) являются противоположными вершинами квадрата. Определить координаты других вершин | |
| Известны одна из вершин треугольника (4;-5), уравнения высоты 7х - у + 17=0 и медианы 2x-11у – 13=0. Составить уравнения сторон | |
| Составить уравнения сторон треугольника, зная одну его вершину (4;1), уравнения высоты 2 х- у + 11 =0 и биссектрисы 7х - 8у + 25=0, проведенных из одной вершины | |
| Стороны треугольника заданы уравнениями: 4х-3у=0 (АВ); 3х -4у=0 (ВС); 5х+ 12у - 10 =0 (АС). Найти радиус описанной окружности | |
| Известны уравнение одной из сторон правильного треугольника 5х-у+1=0 и одна из вершин (5;-3). Составить уравнения двух других сторон треугольника | |
Диагонали ромба пересекаются в точке К (3;-7). Большая диагональ образует с осью ординат угол 46°, а со сторонами 30°. Длина стороны равна 4 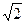 .Составить уравнения сторон ромба .Составить уравнения сторон ромба
| |
Точка М(6;1) является серединой одного из оснований прямоугольной трапеции, а точка N( ;1)-
серединой средней линии. Боковая сторона, перпендикулярная основаниям, лежит на прямой х + + 4у + 7= 0. Составить уравнения остальных сторон трапеции ;1)-
серединой средней линии. Боковая сторона, перпендикулярная основаниям, лежит на прямой х + + 4у + 7= 0. Составить уравнения остальных сторон трапеции
| |
| Из одной вершины треугольника проведена биссектриса 3х + у – 1=0, из другой - медиана 11х - - 5у – 25=0, а третья вершина-точка А(-3;-2). Составить уравнения сторон треугольника | |
| Ортоцентр треугольника - точка Q(-1;5),Составить уравнения сторон треугольника, если известны две его вершины А(2;1) и В(2;11) | |
| Даны уравнения сторон треугольника х + 2у + 1=0; 2х - у - 2 =0, 2х+ y + 2= 0.Найти точку пересечения высот. | |
| Найти координаты центра окружности, проходящей через точку А (-3;5) и касающейся прямых х - 3у- 2 =0 и 13х - 7у + 102=0. |
Задание 4.
В пространстве даны точки А(-2;α1;1), B(3;α2;-1), C(5;α3;1), S(1;α1;0). Сделать чертеж пирамиды SABC и найти:
а) длину и уравнение ребра AB;
б) площадь и уравнение грани ABC;
в) высоту, проведенную из вершины S к грани ABC, и ее уравнение;
г) проекцию вершины S на плоскость ABC;
д) уравнение прямой, проходящей через вершину S параллельно ребру АВ;
е) уравнение плоскости, проходящей через вершину S параллельно грани АВС;
ж) уравнение плоскости, проходящей через ребро AS перпендикулярно грани АВС;
з) уравнение проекции ребра AS на грань АВС;
и) угол между ребрами АВ и AS;
к) угол между ребром AS и гранью АВС;
л) угол между гранями АВС и ABS;
м) координаты центра и радиус вписанной в пирамиду SABC сферы;
н) координаты центра и радиус описанной около пирамиды SABC сферы;
о) координаты центра (тяжести) пирамиды SABC;
п) объем пирамиды.
Задание 5.
Дана точка М(1;0;-2). Найти:
а) точку М1 (x1;y1;z1), симметричную точке М относительно точки S(α1;α2;α3);
б) точку М2 (x2;y2;z2), симметричную точке М относительно прямой
 ;
;
в) точку М3(x3;y3;z3), симметричную точке М относительно плоскости
α1·x + α2·y+α3·z +1=0.
Задание 6.
Составить каноническое уравнение кривой второго порядка (эллипса, гиперболы или параболы (см. табл. 1.4.)), рассоложенной симметрично относительно декартовой системы координат, если ……..(доп. усл. см. табл. 1.5.). Построить кривую на чертеже и указать на нем фокусы и директрисы (для гиперболы еще и асимптоты) кривой.
Таблица 1.4.
ИНДИВИДУАЛЬНЫЕ УСЛОВИЯ К ЗАДАНИЮ 6.
| MOD (n,3) | Кривая | Расположение кривой относительно декартовой прямоугольной системы координат |
| Эллипс | Симметрично относительно начала координат. Фокусы лежат на оси Ox. | |
| Гипербола | Симметрично относительно начала координат. Фокусы лежат на оси Ox. | |
| Парабола | Симметрично оси Ox. Фокусы лежат на оси Ox. |
Таблица 1.5.
ДОПОЛНИТЕЛЬНЫЕ УСЛОВИЯ К ЗАДАНИЮ 6.
| n | Дополнительные условия |
| большая полуось а = 3 и фокусы имеют координаты F(±2;0) | |
| Фокусы имеют координаты F(±5;0) и расстояние между директрисами равно 6 | |
| фокальный параметр равен 3,5 и парабола лежит в полуплоскости х>0 | |
| малая полуось d= 2 и уравнение директрис х =4 | |
| фокальный параметр р = 5 и действительная полуось a = 6 | |
| уравнение директрисы х = -1,5 | |
| большая полуось а = 4 и фокальный параметр р = 6 | |
| действительная полуось а = 4 и расстояние между фокусами равно 10 | |
| точка М(-1;2) принадлежит кривой | |
| фокальные радиусы вершин эллипса, лежащих на оси х, равны 1 и 11 (r 1 =1, r 2 =11) | |
| фокусы имеют координаты Р(±7;0) и уравнение директрис х = ±4 | |
фокус имеет координаты F( ;0) ;0)
| |
малая полуось b= 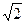 и расстояние между фокусами равно 2 и расстояние между фокусами равно 2
| |
| расстояние между фокусом и соответствующей ему директрисой р =0,5 и фокусы имеют координаты F(±6;0) | |
| уравнение директрисы х = 0,25 | |
| расстояние между фокусами равно 4 и расстояние между директрисами равно 6 | |
действительная полуось равна  и эксцентриситет равен и эксцентриситет равен 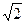
| |
| фокальный параметр р = 1,25 и парабола лежит в полуплоскости х ‹ 0 | |
| фокусы имеют координаты F(±3;0) и расстояние фокусов до соответствующих им директрис р = 1 | |
| действительная полуось а = 3 и уравнение асимптот у = ±2х | |
| парабола проходит через точку М(4;1) | |
большая полуось а =  и эксцентриситет равен и эксцентриситет равен 
| |
расстояние между директрисами равно 2 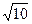 и уравнение асимптот у = ±3х и уравнение асимптот у = ±3х
| |
| фокус имеет координата F(-1;0) | |
эксцентриситет равен  и расстояние между директрисами равно 10 и расстояние между директрисами равно 10
| |
| фокальные радиусы вершин r 1 =5 и r 2 = 7 | |
директриса имеет уравнение х = 
| |
| малая полуось b=3 и фокальный параметр р = 9 | |
| расстояние между фокусами равно 12 и эксцентриситет равен 2 | |
| парабола проходит через точку М(-4;2) | |
| фокусы имеют координаты F(±2;0) и эксцентриситет равен 0,5 | |
мнимая полуось b =  и расстояние между директрисами равно 2 и расстояние между директрисами равно 2 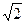
| |
| фокус имеет координаты F(1,5;0) | |
| расстояние между фокусами равно 4, а расстояние между директрисами равно 6 | |
фокусы имеют координаты F(±3;0) и уравнения асимптот y = 
| |
| фокальный параметр равен 3 и парабола расположена в полуплоскости х < 0 | |
уравнения директрис х = ± 4 и фокальный радиус вершин, лежащих на оси у, равен 2 
| |
мнимая полуось b= 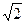 и расстояние между соответствующими друг другу фокусами и директрисами равно 0.5 и расстояние между соответствующими друг другу фокусами и директрисами равно 0.5
| |
| уравнение директрисы х = 1,25 | |
малая полуось b = 2 и эксцентриситет равен 
| |
| мнимая полуось b = 2 и фокусы имеют координата F(3;0) | |
| парабола проходит через точку М(1;4) | |
| большая полуось a = 2 и расстояние между директрисами равно 3 | |
мнимая полуось b = 2 и эксцентриситет равен 
| |
фокус имеет координаты F(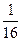 ,0) ,0)
| |
и фокальный радиус вершин эллипса, расположенных на оси Оy, равен 
| |
эксцентриситет равен 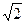 и расстояние между директрисами равно 2 и расстояние между директрисами равно 2
| |
| расстояние между фокусом и директрисой равно 1,5 и парабола расположена р полуплоскости х > 0 | |
эксцентриситет равен  и фокальный радиус вершин эллипса, расположенных на оси Оу, равен 6 и фокальный радиус вершин эллипса, расположенных на оси Оу, равен 6
| |
| мнимая полуось b = 6 и уравнения асимптот у =1.5 х | |
| уравнение директрисы х = -0.75 | |
| расстояние между фокусами равно 6 и фокальный радиус вершин эллипса, расположенных на оси Оу, равен 4 | |
| действительная полуось а = 2 и уравнения директрис х = ± 1 | |
| точка М(-8:2) принадлежит параболе | |
большая полуось а =  и расстояние между фокусами равно 4 и расстояние между фокусами равно 4
| |
| фокальные радиусы вершил гиперболы, расположенных на оси их, равны 4 и 8 | |
| фокус имеет координаты F(0,125;0) | |
малая полуось b = 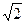 и расстояние между директрисами равно 6 (расстояние между фокусами меньше 3) и расстояние между директрисами равно 6 (расстояние между фокусами меньше 3) 
| |
действительная полуось а = 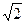 и фокусы имеют координаты F(±5:0) и фокусы имеют координаты F(±5:0)
| |
| фокальный параметр равен 0,25 и парабола расположена в полуплоскости х < 0 | |
| малая полуось b = 2 и фокусы имеют координаты F(±3;0) | |
эксцентриситет равен  и уравнение директрис х = ±2 и уравнение директрис х = ±2
| |
уравнение директрисы х = 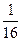
| |
большая полуось а = 2 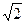 и эксцентриситет равен 0,5 и эксцентриситет равен 0,5
| |
мнимая полуось b = 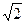 и расстояние между фокусами равно 4 и расстояние между фокусами равно 4
| |
| точка М(2;3) принадлежит параболе | |
| фокальные радиусы вершин эллипса, расположенных на оси Ох, равны 3 и 7 | |
действительная полуось а = 2 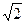 и эксцентриситет равен 2 и эксцентриситет равен 2
| |
| фокус имеет координаты F(-2,5;0) | |
| малая полуось b = 3 и эксцентриситет равен 0.5 | |
| фокальный параметр равен 3 и расстояние между фокусами равно 10 | |
| расстояние между фокусом и директрисой равно 0,25 и парабола расположена в полуплоскости х > 0 | |
эксцентриситет равен  и расстояние между фокусами равно 2 и расстояние между фокусами равно 2
| |
действительная полуось а =  и уравнения асимптот у = ± 2/3 · и уравнения асимптот у = ± 2/3 ·  ·x ·x
| |
| уравнение директрисы х = 1 | |
большая полуось равна  и расстояние между директрисами равно 7 и расстояние между директрисами равно 7
| |
| мнимая полуось b = 3 и эксцентриситет равен 2 | |
| парабола переходит через точку М(3;6) | |
| расстояние между фокусами равно 6 и уравнения директрис х = ±5 | |
мнимая полуось b = 2  и фокальный параметр р = 3 и фокальный параметр р = 3
| |
| фокус имеет координаты F(0,5;0) | |
| эксцентриситет равен 0,5 и уравнения директрис х = ± 6 | |
расстояние между фокусами равно  и уравнения асимптот у = ± х и уравнения асимптот у = ± х
| |
| расстояние между фокусом и директрисой равно 3,5 и парабола расположена в полуплоскости х < 0 | |
малая полуось b = 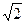 и фокальный радиус вершин эллипса. расположенных на оси Оу, равен и фокальный радиус вершин эллипса. расположенных на оси Оу, равен 
| |
| фокусы имеют координаты Р(19;0) и эксцентриситет равен 3 | |
| уравнение директрисы x = -1 | |
| фокальный параметр равен 3 и расстояние между фокусами равно 4 | |
| действительная полуось а = 4 и расстояние между директрисам равно 4 | |
| парабола проходит через точку М(-4;5) | |
| фокусы имеют координаты F(±4;0) и фокальные радиусы вершин эллипса, расположенных на оси Оу, равны 5 | |
мнимая полуось b =  и уравнения асимптот y = и уравнения асимптот y = 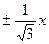
| |
| фокус имеет координаты F(1;0) | |
расстояние между директрисами равно 10 и фокальные радиусы вершин на оси Оу равны 
| |
расстояние между директрисами равно  и уравнение асимптот у = ±0,5х и уравнение асимптот у = ±0,5х
| |
| фокальный параметр равен 2,5 и парабола расположена в полуплоскости х > 0 | |
малая полуось b =  и фокальный параметр р = 5 и фокальный параметр р = 5
| |
мнимая полуось b = 2 и уравнения директрис
x = ± 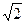
| |
| фокус имеет координаты F(-0,5;0) | |
| большая полуось а = 2 и фокальный параметр р = 3 |
ЗАДАНИЕ 7.
Составить уравнение линии, для каждой точки М, которой отношение расстояния до точки F( ;
;  ) и до прямой х =
) и до прямой х =  равно е =
равно е =  . Привести уравнение к каноническому виду, определить тип линии и построить линию на чертеже. Показать на чертеже фокусы, директрисы, асимптоты (если они имеются у построенной линии).
. Привести уравнение к каноническому виду, определить тип линии и построить линию на чертеже. Показать на чертеже фокусы, директрисы, асимптоты (если они имеются у построенной линии).
Задание 8.
Линия задана уравнением r =  в полярной системе координат (см. табл. 1.6, 1.7.).Требуется:
в полярной системе координат (см. табл. 1.6, 1.7.).Требуется:
а) построить линию по точкам, начиная от φ = 0 до φ = 2π и придавая φ значения с шагом ∆φ =  ;
;
б) найти уравнение линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью;
в) привести уравнение кривой в декартовой прямоугольной системе координат к каноническому виду, определить какая это линия.
Таблица 1.6.
ФУНКЦИЯ f(φ) К ЗАДАНИЮ 8.
| MOD(n,2) | f(φ) |
| cos φ sin φ |
ПАРАМЕТРЫ a, b, c К ЗАДАНИЮ 8.
| n | a | b | c | n | a | b | c |
| -3 -1 -3 -3 -1 -1 -4 -2 -1 -4 -2 -1 -4 -3 -3 -3 -1 -2 -1 -4 -1 -5 -4 | -5 -2 -1 -3 -4 -1 -2 -2 -1 -1 -5 -1 -4 -1 -4 -2 -4 -2 -1 -5 -2 -3 -1 -4 |
 1.2.9. Задание 9. Построить поверхность второго порядка.
1.2.9. Задание 9. Построить поверхность второго порядка.
Уравнение поверхностей к заданию 9
| Вари- ант | 1-е уравнение | 2-е уравнение | Вари- ант | 1-е уравнение | 2-е уравнение |

| 
| 
| 
| ||

| 
| 
| 
| ||
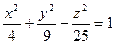
| 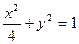
| 
| 
| ||

| 
| 
| 
| ||

| 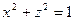
| 
| 
| ||

| 
| 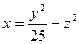
|   
| ||
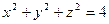
| 
| 
| 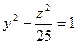
| ||

| 
| 
| 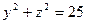
| ||

| 
| 
| 
| ||

| 
| 
| 
| ||

| 
| 
| 
| ||

| 
| 
| 
| ||

| 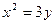
| 
| 
| ||

| 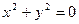
| 
| 
| ||

| 
| 
| 
| ||

| 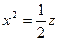
| 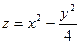
| 
|
Продолжение таблицы

| 
| 
| 
| ||

| 
| 
| 
| ||

| 
| 
| 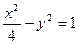
| ||

| 
| 
| 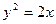
| ||

| 
| 
| 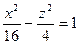
| ||

| 
| 
| 
| ||

| 
| 
| 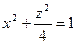
| ||

| 
| 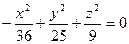
| 
| ||

| 
| 
|  
| ||

| 
| 
| 
| ||

| 
| 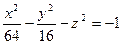
| 
| ||

| 
| 
| 
| ||

| 
| 
| 
| ||

| 
| 
| 
| ||

| 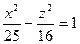
| 
| 
| ||

| 
| 
| 
| ||

| |||||
|
|
|
|
|
Дата добавления: 2016-10-30; Мы поможем в написании ваших работ!; просмотров: 757 | Нарушение авторских прав
Лучшие изречения:






