1. Работа в печатной тетради № 2.
Задание № 182.
– Прочитайте текст. Можно ли его назвать задачей?
– Что известно?
– Поставьте вопрос к условию задачи так, чтобы она решалась делением. (Во сколько раз у Вити марок больше, чем у Миши? Во сколько раз у Миши марок меньше, чем у Вити?)
Решение:
54: 9 = 6 (раз).
– Объясните, что обозначают выражения:

2. Работа по учебнику.
Задание № 28 (с. 115).
– Прочитайте текст задачи.
– Что известно?
– Что требуется узнать?
– Запишите кратко условие задачи.
Запись:

Решение:
1) Какова высота чайника?
18 + 9 = 27 (см).
2) Во сколько раз высота чайника выше высоты кружки?
27: 9 = 3 (раза).
Ответ: в 3 раза выше.
3. Решение математического кроссворда.
По горизонтали:
3. Период в 100 лет. (Век.)
4. Результат сложения. (Сумма.)
6. Четырехугольник, у которого все углы прямые. (Прямоугольник.)
8. Что получится, если к разности прибавить вычитаемое? (Уменьшаемое.)
9. Результат вычитания. (Разность.)
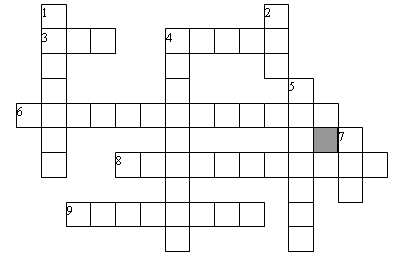
По вертикали:
1. Прямоугольник, у которого все стороны равны. (Квадрат.)
2. Промежуток времени, равный 60 минутам. (Час.)
4. Что получится, если из суммы вычесть слагаемое. (Слагаемое.)
5. Прибор для измерения длины предметов. (Линейка.)
7. Промежуток времени, равный 12 месяцам. (Год.)
VI. Итог урока.
Домашнее задание: № 35, 36 (учебник); № 177 (рабочая тетрадь).
Урок 124
Повторение по теме
«ФИГУРЫ И ВЕЛИЧИНЫ»
Цели: совершенствовать умения и навыки решения геометрических задач на нахождение периметра и площади; закреплять знание определений и основных свойств геометрических фигур; развивать пространственное мышление.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Отгадайте загадку.
В сенокос горька,
А в мороз сладка.
Что за ягодка?
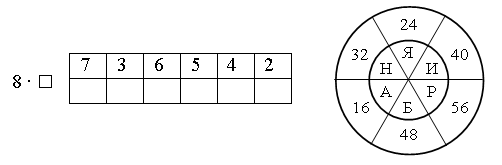
2. Вставьте арифметические знаки так, чтобы равенства были верными.

3. Из каждого столбика выберите «лишнее» число.
6 32 66
18 28 88
24 16 77
2229 55
30 24 13
4. Сколько треугольников лежит внутри круга, сколько пересекается с кругом, сколько лежит вне круга?

III. Сообщение темы урока.
IV. Работа по теме урока.
- Работа по учебнику.
Задание № 1 (с. 104) выполняется устно.
На доске можно составить схему:
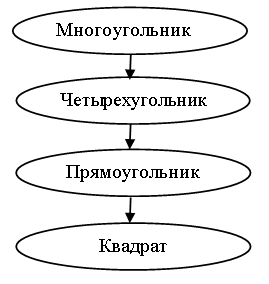
Опираясь на данную схему, учащиеся называют свойства и дают определения.
Задание № 2 (с. 104).
учащиеся выполняют самостоятельно. Взаимопроверка в парах.
Задание № 3 (с. 105).
учащиеся соединяют верные утверждения с геометрической фигурой.
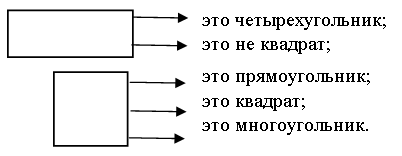
Задание № 4 (с. 105).
Учащиеся определяют верность утверждений.
• Любой квадрат является прямоугольником. (Да.)
• Не любой прямоугольник является квадратом. (Да.)
• Среди четырехугольников есть прямоугольники. (Да.)
• Квадрат – это не прямоугольник. (Нет.)
• Бывают прямоугольники с четырьмя равными сторонами. (Да.)
Задание № 5 (с. 105).
Чертеж:
– Сколько осей симметрии у квадрата? (4 оси симметрии.)

Задание № 8 (с. 106).
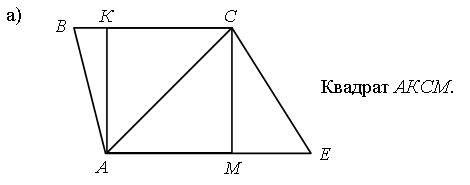
– Сколько треугольников на чертеже?
– Сколько четырехугольников на чертеже?
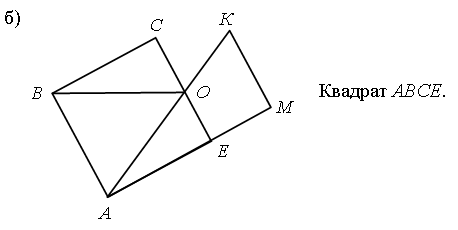
Задание № 9 (с. 106).
Утверждение: «Если два квадрата имеют общую сторону, то эти квадраты равны» – верно.
Учащиеся выполняют построение в тетради и проверяют данное утверждение.
Задание № 10 (с. 106).
– Какая фигура является пересечением (общей частью):
а) квадрата и луча?
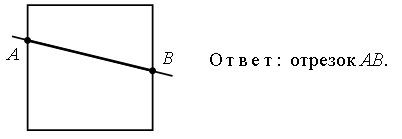
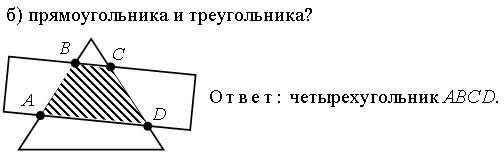
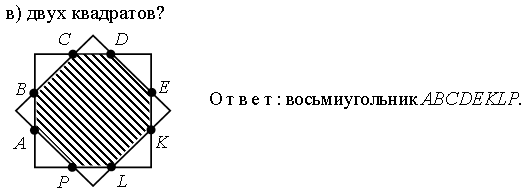
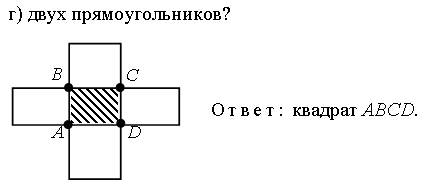
Задание № 11 (с. 106).
– Рассмотрите чертежи и назовите отрезки, которые являются диагоналями прямоугольника АВМС.
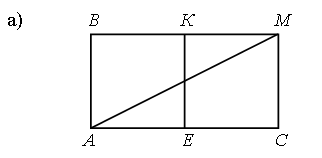
Ответ: АМ.
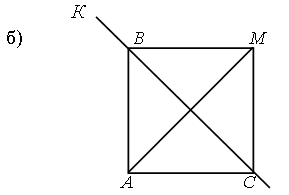
Ответ: АМ и ВС.
– Назовите основные свойства прямоугольника.
– Что такое диагональ прямоугольника?
– Назовите свойства диагоналей прямоугольника.
2. Работа в печатной тетради № 2.
Задание № 191.
Учащиеся проводят оси симметрии каждой фигуры:
Чертеж:
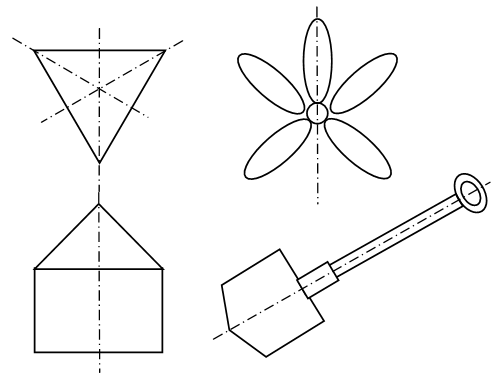
– Сколько осей симметрии имеет треугольник? (Три оси симметрии.)
– Почему? (У данного треугольника все стороны равны.)
– Почему текст письма не имеет ни одной оси симметрии?
Задание № 192.
– Назовите признаки окружности.
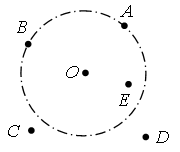
– Пройдет ли окружность с центром в точке О через каждую красную точку?
Далее учащиеся выполняют построение с помощью циркуля.