II. Устный счет.
1. Чем похожи и чем отличаются друг от друга числа в каждой паре:
| 12 и 13 | 62 и 26 | 42 и 62 |
| 13 и 14 | 37 и 73 | 57 и 79 |
2. По какому правилу записан каждый ряд чисел:
а) 90, 60, 70, 40, 50, 20, 30, 0, 10;
б) 10, 30, 20, 40, 30, 50, 40, 60, 50.
3. Найдите значения выражений:
30 + 20 – 40 + 60 – 50 + 20 + 40 = 
80 – 30 – 10 + 50 – 70 + 60 – 80 =
90 – 60 + 20 – 40 + 60 + 20 – 50 =
30 + 40 – 60 + 80 – 20 – 60 + 10 =
20 + 70 – 50 + 30 – 60 + 80 – 90 =
4. Сколько отрезков с отмеченными концами можно найти на этом рисунке?
III. Сообщение темы урока.
– Сравните выражения каждого столбика:
| 25 + 12 | 25 + 19 |
| 46 + 24 | 46 + 25 |
– Чем отличаются выражения первого столбика от выражений второго столбика?
– Сегодня на уроке рассмотрим сложение двузначных чисел в пределах 100 с переходом через десяток.
IV. Изучение нового материала.
Подготовительные задания:
1) Назовите число, которое на 1 больше каждого из чисел:
6, 4, 8, 7, 0, 2, 9, 1, 5, 3.
2) Число 6 можно записать так: 
. Какое число означает каждая из записей: 
?
Примечание.
Очень важно выработать у учащихся умение воспринимать подобные записи. Например, как запись числа 6, являющегося суммой 5 и 1. Во-первых, это предупредит весьма распространенную ошибку, допускаемую детьми: в тех случаях, когда при сложении единиц в результате получается число, большее 10, они, сложив десятки, забывают прибавлять к ним еще 1 десяток. Во-вторых, представляется возможность сократить число шагов алгоритма сложения, что тоже немаловажно для выработки скорости вычислений.
Задание № 1 (с. 56).
– Рассмотрите рисунок на с. 56 и объясните, как Волк и Заяц выполняли сложение вида 27 + 15.
Один из учащихся рассказывает, что и как выполняют Волк и Заяц, а остальные дети работают параллельно, используя наборы оранжевых и белых палочек.
Задача: найти сумму 27 и 15.
Волк и Заяц составили «поезд» из 2 оранжевых и 7 белых «вагонов» и «поезд» из 1 оранжевого и 5 белых «вагонов». Затем к первому «поезду» они прицепляют слева один оранжевый, а справа – 5 белых «вагонов» из второго «поезда». Получился новый «поезд», в котором 3 оранжевых и 12 белых «вагонов». Но 12 – это 1 десяток и 2 единицы. Поэтому Волк и Заяц десяток белых «вагонов» заменили одним оранжевым «вагоном».
Длина «поезда» не изменилась. Получилось 4 оранжевых и 2 белых «вагона». Поезд обозначает число 42. Значит, сумма 27 и 15 равна 42.
Далее переходите к рассмотрению записи сложения этих чисел столбиком.
7 + 5 – двенадцать: 1 десяток (пишем маленькую цифру 1 над цифрой 2) и 2 единицы (пишем 2 под 5), 3 + 1 – четыре (пишем 4 под 1). Получается 42. В дальнейшем можно сократить рассуждение, сделать его более лаконичным.
Рассмотрите со всем классом следующие примеры:
Пример 1: сложить 64 и 29.
Объяснение: 4 + 9 – тринадцать: 1 десяток 3 единицы, 7 + 2 – девять. Сумма 93.
Пример 2: сложить 75 и 6.
Объяснение: 5 + 6 – одиннадцать: 1 десяток 1 единица, 8 + 0 – восемь. Сумма 81.
Пример 3: сложить 4 и 58.
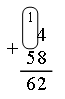
Объяснение: 4 + 8 – двенадцать: 1 десяток 2 единицы, 1 + 5 – шесть. Сумма 62.
Задание № 2 (с. 57).
Учащиеся работают в парах. Используя цветные палочки, они находят значение сумм с переходом через десяток.
Задание № 3 (с. 57).
Учащиеся выполняют задание с комментированием у доски, записывая сложение чисел в столбик.
