II. Устный счет.
1. Игра «Веселый счет».
2. Поставьте знак «+» или «–» так, чтобы равенства были верными.
| 3 … 4 = 7 | 10 … 2 = 12 | 98 … 6 = 92 |
| 4 … 3 = 1 | 10 … 2 = 8 | 89 … 3 = 86 |
| 9 … 6 = 3 | 30 … 9 = 39 | 37 … 1 = 38 |
| 5 … 3 = 8 | 67 … 2 = 65 | 22 … 4 = 26 |
3. Сравните тексты задач. Чем они похожи? Чем отличаются? Решите задачи.
| Из одного старого дома выехали в новые дома 9 семей, из другого – 4. На сколько семей уменьшилось население старых домов? | Из одного старого дома выехали в новые дома 9 семей, из другого – 4. Сколько всего семей переехало в новые дома? |
III. Сообщение темы урока.
– Прочитайте данные на доске записи:
| 2 + 5, | АВ, |
| 8 – y, | О (3). |
– Какие у вас возникли затруднения?
– Сегодня на уроке мы узнаем, что обозначает запись О (3).
IV. Работа над новым материалом.
Задание № 5 (с. 24).
– Что изображено на рисунке?
– Что называют числовым лучом?
– Прочитайте его название. (ОВ.)
– Какие числа соответствуют точкам М, К, А, В? (М – число 2, К – число 5, А – число 6, В – число 9.)
– Как же называются эти числа?

– Итак, координата – это число. Давайте рассмотрим таблицу в учебнике на с. 25. Точка О, ее координата – нуль. Запись О (0) читают так: «Точка О с координатой нуль» или «Точка О имеет координату нуль».
– Прочитайте таблицу до конца.
– Прочитайте записи в таблице: М (2) и А (6).
– Запишите в тетради координаты остальных точек.
Запись: К (5), В (9).
– А теперь научимся изображать числовой луч. Необходимо помнить о том, что числовой луч всегда чертят строго горизонтально в направлении слева направо. Направление надо указывать стрелкой.
Задание № 4 (с. 24).
– Итак, проводим горизонтально луч, обозначим его буквами ОX, указываем направление стрелкой, под точкой О напишем число 0 (нуль).
Далее выбираем единичный отрезок (2 см) и откладываем на луче единичный отрезок. Расставим точки.
– Рассмотрите числовой луч на с. 24.
– Числа можно сравнивать с помощью числового луча. Сравните длины отрезков ОА и ОВ на числовом луче ОX. (Длина отрезка ОА равна 5 единичным отрезкам, а длина отрезка ОВ равна 7 единичным отрезкам. На луче точка А лежит левее точки В, отрезок ОА меньше отрезка ОВ, т. е. 5 меньше 7.)
Задание № 6 (с. 25).
– Рассмотрите рисунок. Прочитайте координаты точек, где сидят улитки. (Точка М с координатой 2; точка К с координатой 6; точка В с координатой 8; точка С с координатой 11.)
– Какая точка находится левее: М (2) или В (8)?
– Какая точка имеет наибольшую координату?
V. Повторение пройденного материала.
1. Работа в печатной тетради № 1.
Задание № 31.
Учитель должен обратить внимание учащихся на то, что единичный отрезок равен 2 клеткам (или 1 см). Значит, чтобы отметить точку С с координатой 3, надо от начала луча отсчитать 3 раза по 2 клетки:

Чертеж:

Задание № 33.
– Рассмотрите верхний числовой луч. Что вы можете о нем сказать? (От начала луча отложены равные по длине отрезки, причем единичный отрезок содержит в себе два таких отрезка.)
– Сколько единичных отрезков укладывается от начала луча до точки А? (6 единичных отрезков, значит, координата точки А равна 6.)
– До точки В? (В(8).)
– До точки С? (С(12).)

– Рассмотрите нижний числовой луч. Что вы можете о нем сказать? (Здесь изображена часть числового луча, нет точки 0, т. е. начала луча. И не указан единичный отрезок.)
– Как можно восстановить единичный отрезок? (На этом числовом луче отмечены точки Е(45) и А(48). Отрезок между этими точками содержит три единичных отрезка. Разделим длину отрезка ЕА на 3, получим единичный отрезок.)
Чертеж:

2. Работа по учебнику.
Задание № 15 (с. 27).
– Рассмотрите чертеж. Что на нем изображено?
– На какие отрезки разбивает отрезок АВ точка М?
– На какие отрезки разбивает отрезок АВ точка С?
– Сколько всего отрезков на чертеже? (Всего шесть отрезков: АВ, АМ, АС, ВС, ВМ, МС.)
– Из суммы длин каких трех отрезков складывается длина отрезка АВ?
– Длины каких отрезков нам известны?
– Длину какого отрезка надо найти?
– Запишите решение этой задачи.
Решение:
| I способ: | II способ: |
| 1) 6 + 3 = 9 (см) 2) 18 – 9 = 9 (см) Ответ: МС = 9 см. | 1) 18 – 6 = 12 (см) 2) 12 – 3 = 9 (см) |
Задание № 16 (с. 27).
– Какое отношение изображено на первом графе? (Отношение «меньше».)
– Прочитайте все высказывания о числах на этом графе. (50 меньше 98; 34 меньше 50; 34 меньше 98; 34 меньше 41; 41 меньше 50; 41 меньше 90.)
– Какое отношение показано на втором графе? (Отношение «больше».)
– Прочитайте все высказывания о числах на этом графе. (Учащиеся должны прочитать шесть высказываний, так как здесь три стрелки и три петли: 78 больше 65; 96 больше 65; 96 больше 78; 78 равно 78; 65 равно 65; 96 равно 96.)
Задание № 19 (с. 28).
– Прочитайте задачу.
– Что известно в задаче? Что надо узнать?
– Запишите кратко условие задачи.

– Какое арифметическое действие надо выбрать, чтобы ответить на вопрос «на сколько меньше»?
– Запишите решение этой задачи.
Задание № 20 (с. 28).
– Прочитайте задачу.
– Сколько грибов нашла Таня? (9 грибов.)
– Что сказано про количество грибов у Лиды? (На 5 грибов меньше, чем Таня.)
– Прочитайте, что требуется узнать.
– Запишите кратко условие задачи и решите ее.
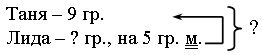
Решение:
1) 9 – 5 = 4 (гр.) – нашла Лида.
2) 9 + 4 = 13 (гр.) – всего.
Ответ: 13 грибов.
VI. Итог урока.
– Что нового узнали на уроке?
– Что называют координатой?
– Как можно сравнивать числа, используя числовой луч?
Домашнее задание: № 17, 18 (учебник); № 31, 33 (рабочая тетрадь).
Урок 12
Числовой луч
Цели урока: закрепить умение чертить числовой луч, выбирать единичный отрезок, отмечать точки с заданными координатами; совершенствовать навык сравнения чисел с использованием числового луча; рассмотреть способы восстановления числового луча; совершенствовать вычислительные навыки; развивать внимание и память.
Ход урока






