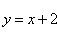

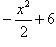 .
.
В) Вычислить площадь фигуры, ограниченной линиями  ,
, 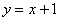 ,
,  ,
,  .
.
Решение: Сначала выполним чертеж:

Фигура, площадь которой нам нужно найти, заштрихована синим цветом (внимательно смотрите на условие – чем ограничена фигура!). Но на практике по невнимательности нередко возникает сомнение, что нужно найти площадь фигуры, которая заштрихована зеленым цветом!
Этот пример еще полезен и тем, что в нём площадь фигуры считается с помощью двух определенных интегралов. Действительно:
1) На отрезке  над осью
над осью 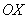 расположен график прямой
расположен график прямой 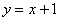 ;
;
2) На отрезке 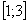 над осью
над осью 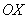 расположен график гиперболы
расположен график гиперболы  .
.
Совершенно очевидно, что площади можно (и нужно) приплюсовать, поэтому:
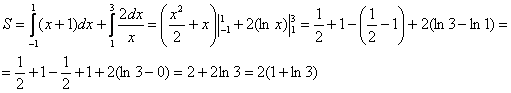
Ответ: 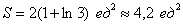
Решение.
Находим точки пересечения заданных линий. Для этого решаем систему уравнений:

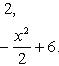
Для нахождения абсцисс точек пересечения заданных линий решаем уравнение:
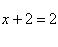
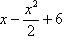 или
или 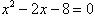 .
.
Находим: x 1 = -2, x 2 = 4.
Итак, данные линии, представляющие собой параболу и прямую, пересекаются в точках A (-2; 0), B (4; 6).
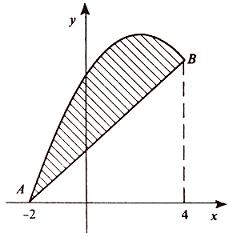
Эти линии образуют замкнутую фигуру, площадь которой вычисляем по указанной выше формуле:



По формуле Ньютона-Лейбница находим:


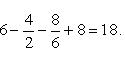
Пример 7.
a) Необходимо найти определенный интеграл

Имеем:
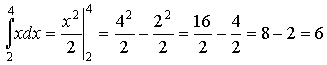
Таким образом искомый интеграл равен 6.
b)Вычислить интеграл: 
Решение:
 =(3
=(3 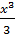 + 4
+ 4 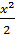 +5x)
+5x) 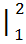 =
=  +2
+2 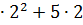 -
-
- (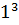 +2
+2  26- 8=18.
26- 8=18.
Пример 8. Найти неопределенные интегралы:

Решение
При решении примеров следует пользоваться свойствами неопределенных интегралов, таблицей интегралов, в которую включена формула интеграла функции линейного аргумента, непосредственным интегрированием и методом подстановки.
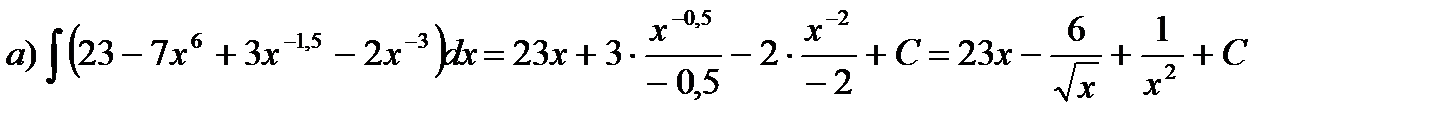
б) Выполнив почленное деление в подынтегральной функции, получим:

в)
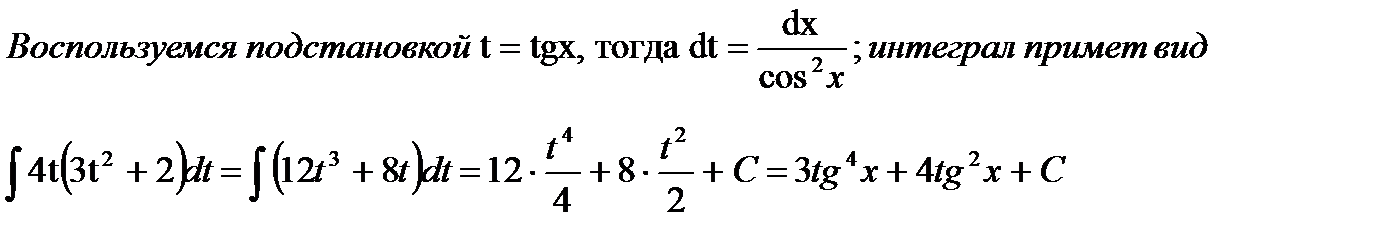
г) Будем использовать подстановку:
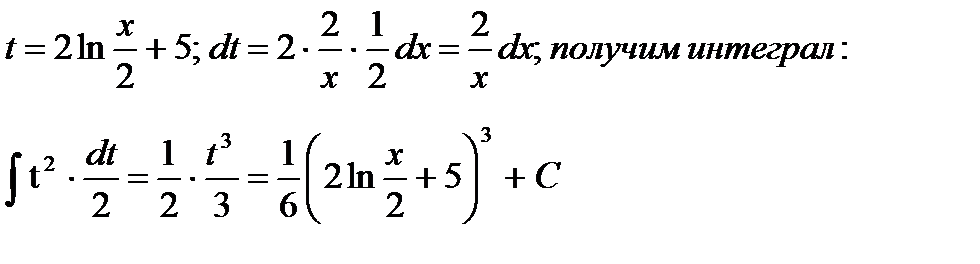
д) Воспользуемся подстановкой:
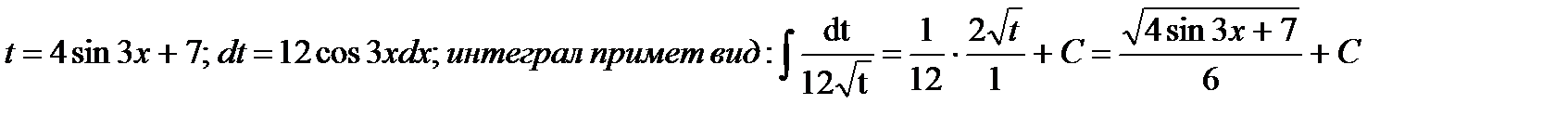
1) Вычислить определенные интегралы:
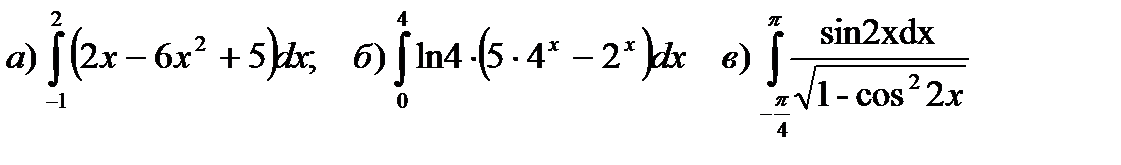
Решение
При вычислении определенных интегралов используем формулу Ньютона-Лейбница
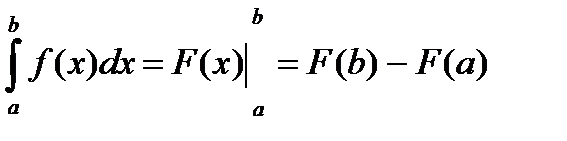 . Получение первообразной функции F(x) будем выполнять или непосредственно или способом подстановки.
. Получение первообразной функции F(x) будем выполнять или непосредственно или способом подстановки.
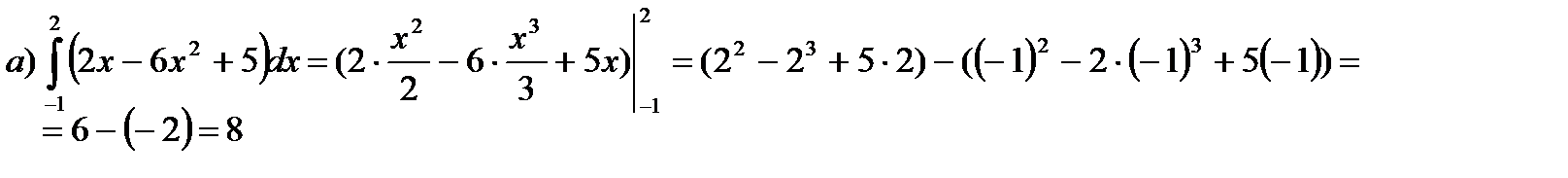
б)
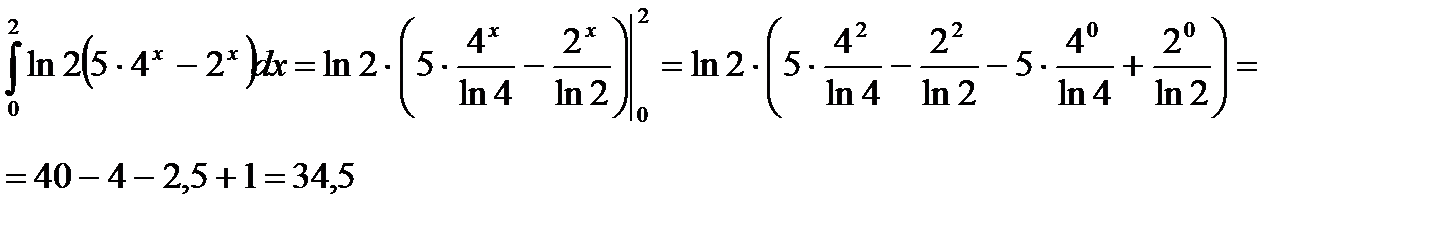


Пример 8.
1) Выполнить действия сложения, вычитания, умножения, деления над комплексными числами в алгебраической форме.
Z1=3+4i, Z2=2i18-5i15
Решение
Предварительно преобразуем второе число, используя значения степеней мнимой единицы. i18=i16+2=i16i2=1i2=-1, i15=i12+3=i12i3=i3=-i, Z2=-2+5i
Выполним действия над числами:
Z1+Z2=(3+4i)+(-2+5i)=3+4i-2+5i=(3-2)+(4i+5i)=1+9i
Z1-Z2=(3+4i)-(-2+5i)=3+4i+2-5i=(3+2)+(4i-5i)=5-I
Z1 .Z2=(3+4i) . (-2+5i)=-6+15i – 8i +20i2=-6+7i – 20= - 26 + 7i
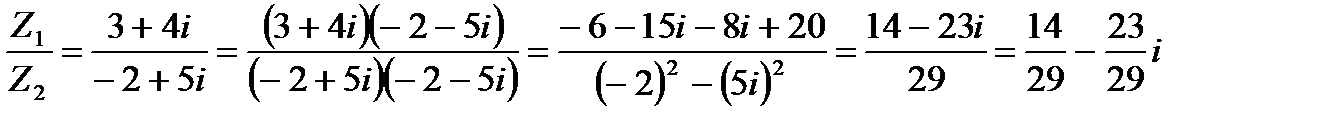
Пример 9.
a) Имеется набор разноцветных шариков, среди которых 5 синих, 3 красных и 2 зеленых. Наугад извлекают 4 шарика. Найти вероятность того, что среди извлеченных шариков 2 синих, 1 красный и 1 зеленый.
Решение
Для определения вероятности случайного события будем использовать классическую формулу  , в которой n – число всех возможных исходов, m- число исходов, благоприятных появлению события. В задаче значения этих величин следует находить при помощи сочетаний.
, в которой n – число всех возможных исходов, m- число исходов, благоприятных появлению события. В задаче значения этих величин следует находить при помощи сочетаний. 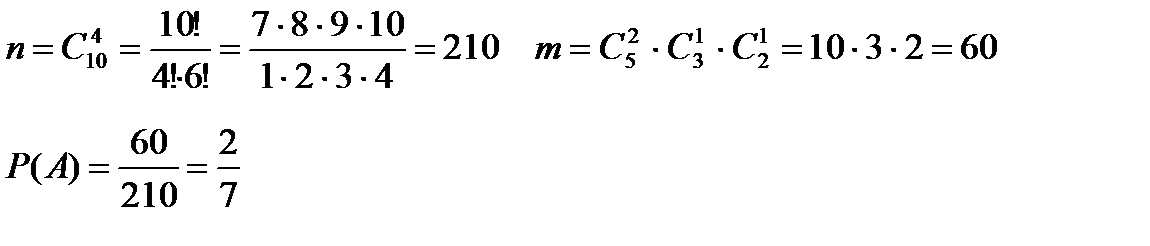
b) Из карточек разрезной азбуки составлено слово «панорама». Карточки перемешали и наудачу по одной извлекают 5 карточек, выкладывая их в порядке извлечения. Найти вероятность того, что окажется составленным слово «роман».
Решение
В этой задаче можно воспользоваться произведением зависимых случайных событий
А – получение слова «роман»;
В1 – извлечение первой карточки с буквой «р»;
В2 – извлечение второй карточки с буквой «о»; и т.д.
Тогда А=В1 . В2 . В3 . В4 . В5
Р(А)=Р(В1) . Р(В2) . Р(В3) . Р(В4) . Р(В5)= 






