| Характеристика источника | Пример оформления |
| Один, два или три автора | Котаў, А.І. Гісторыя Беларусі і сусветная цывілізацыя / А.І. Котаў. – 2-е выд. – Мінск: Энцыклапедыкс, 2003. – 168 с. |
| Чикатуева Л.А. Маркетинг: учеб. пособие / Л.А. Чикатуева, Н.В. Третьякова; под ред. В.П. Федько. – Ростов н/Д: Феникс, 2004. – 413 с. | |
| Дайнеко, А.Е. Экономика Беларуси в системе всемирной торговой организации / А.Е. Дайнеко, Г.В. Забавский, М.В. Василевская; под ред. А.Е. Дайнеко. – Минск: Ин-т аграр. экономики, 2004. – 323 с. | |
| Четыре и более авторов | Культурология: учеб. пособие для вузов / С.В. Лапина [и др.]; под общ. ред. С.В. Лапиной. – 2-е изд. – Минск: ТетраСистемс, 2004. – 495 с. |
| Коллективный автор | Сборник нормативно-технических материалов по энергосбережению / Ком. по энергоэффективности при Совете Министров Респ. Беларусь; сост. А.В. Филипович. – Минск: Лоранж-2, 2004. – 393 с. |
| Военный энциклопедический словарь / М-во обороны Рос. Федерации, Ин-т воен. истории; редкол.: А.П. Горкин [и др.]. – М.: Большая рос. энцикл.: РИПОЛ классик, 2002. – 1663 с. |
Таблица распределения контрольных вопросов и заданий по вариантам
| Предпоследняя цифра шифра | Последняя цифра шифра | |||||||||
| 1,11,21,31 41,51,61 | 2,12,22, 3242,52. | 3,13,23, 3343,53, | 4,14 24,34 44,54,64 | 5,15 25,35 45,55,65 | 6,16 26,36 46,56,66 | 7,17 27,37 47,57,67 | 8,18 28;38 48,58,68 | 9,19 29,39 49,59,69 | 10,20 30,40 50,60,70 | |
| 2,13 24,35 46,57,71 | 3,14 25,36 47,58,72 | 4,25 26,37 48,59,73 | 5,16 28,39 49,60,74 | 6,17 29,36 41,51,75 | 7,18 26,31 41,52,76 | 8,19 21,32 42,53,77 | 9,20 27,33 43,54.78 | 10,11 22,38 44,55,79 | 1,12 23,34 45,56,80 | |
| 3,15 27,39 42,53,81 | 4,16 28,39 43,5,825 | 5,17 29,31 44,55,83 | 6,16 22,32 46,57,84 | 7,19 21,33 46,58,85 | 8,16 22,34 47,56,86 | 9,11 23,35 48,59,87 | 10,12 24,36 49,6,880 | 1,13 25,37 46,51,89 | 2,14 26,38 41,52,90 | |
| 4,17 29,33 48,60,91 | 5,18 21,34 49,51,92 | 6,19 22,35 44,52,93 | 7,16 23,36 41,53,94 | 8,11 24,37 42,54,95 | 9,12 25,38 43,55,96 | 10,13 26,39 44,56,97 | 1,14 27,40 45.57,98 | 2.15 28.31 46.58,99 | 3.16 29.32 47.59,100 | |
| 5.19 23.37 43.56,61 | 6.20 24,38 44,57,62 | 7,11 25,39 45,58,63 | 8,12 26,36 46.59,64 | 9,13 27,31 47,60,75 | 10,14 28,32 47,60,76 | 1,15 29,33 49,52,65 | 2,16 27,34, 46,53,66 | 3,17. 21,35 41,54,67 | 4,18 22,36 42,55,68 | |
| 6,12 26,38 44,52,69 | 7,13 27,39 45,53,70 | 8,14 28,40 46,54,71 | 9,15 29,31 47,55,72 | 10,16 22,32 48,56,73 | 1,17 21,33 49,57,74 | 2,18 22,34 40,58,75 | 3,19 23,35 41,59,76 | 4,12 24,36 42,60,77 | 5,11 25,37 43,51,78 | |
| 7,14 29,32 47,54,79 | 8,15 28,33 48,69,80 | 9,16 21,34 49,56,81 | 10.17 22.35 45.57,82 | 1.18 23.36 41.58,83 | 2.19 24.37 42.59,84 | 3.13 25.38 43.60,85 | 4.11 26.39 44.6 1,86 | 5.12 27.32 45.52,87 | 6.13 28.31 46.6 3,88 | |
| 8,16 22,34 45,55,89 | 9,17 23,35 46,56,90 | 10,18 24,36 47,51,67 | 1.19 25.37 48.58,90 | 2.11 26.38 49.59,81 | 3.14 27.39 50.60,82 | 4.12 28.38 41.51,83 | 5.13 29.31 42.6 2,84 | 6.14 25.32 43.53,85 | 7.15 21.33 44.70,86 | |
| 9,18 25,38 44,68,87 | 10,19 26,31 41,60,71 | 1,16 27,32 42,51,72 | 2.11 28.33 43.52,73 | 3.12 29.34 44.53,74 | 4.13 21.35 45.54,75 | 5.14 21.36 46.65,76 | 6.11 22.37 47.56,77 | 7.16 23.38 48.57,79 | 8.17 24.39 49.64,80 | |
| 4,18 28,38 49,51,60 | 1,11 29,37 44,59,65 | 2,12 26,38 41,55,67 | 3.13 21.39 42.51,66 | 4.14 22.30 43.52,65 | 5.15 23.31 44.53,64 | 6.16 24.32 45.54,63 | 7.17 25.33 46.57,62 | 8.18 26.34 47.66,76 | 9.19 27.35 48.57,69 |


31- 40. Исследовать свойства функции и построить её график
y = 
| |
y = 
| |
y = 
| |
y = 
| |
y = 
| |
y = 
| |
y = 
| |
y = 
| |
y = 
| |
y = 
|
Найти интегралы и проверить результат дифференцированием
41.  42.
42.  43.
43. 
44.  45.
45. 

47.  48.
48. 

50. 
 52.
52. 



56. Проверить, является ли функция 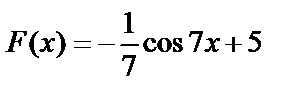 первообразной для функции
первообразной для функции 
57. Докажите, что функция F (x) является первообразной функции f (x) и найдите неопределенный интеграл:
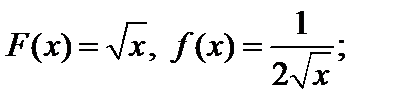
Методом подстановки найти интеграл:
58.  59.
59.  60.
60. 
62-70. Вычислите площадь фигуры, ограниченной линиями:
62.  у= 3х.
у= 3х.
63.  у=-х+7,
у=-х+7,
64. 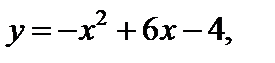 у=2х,
у=2х,
65. у=2х2+4,у= х+5,
66. у=2х-х2 +3, у=х2 - 4х-+3.
67. у=3х2 _4, у=1/2х,
68. у=3х2 _2, у=2х,
69. у=2х+5, у= х2-3,
70. у=х2-4,у= х+3,
71-80. Выполните задание.
71. Укажите произведение элементов  матрицы матрицы 
|
72. Вычислите 
|
73. Укажите сумму элементов матрицы X, являющейся решением уравнения  где где  
|
74. Найти произведение матриц АВ = С, если А, В даны: А =  , В = , В = 
|
75. Укажите сумму элементов матрицы  если если 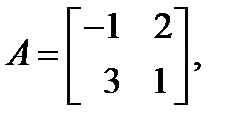 
|
76. Найдите элемент 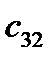 матрицы матрицы  если если  
|
77. Решите уравнение 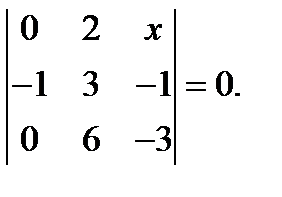
|
78. Укажите сумму элементов матрицы  если если  
|
79.. Укажите сумму элементов матрицы, обратной данной 
|
80. Вычислите 
|
Выполнить действия
| (1+3i)+(-3+i) | (5-3i)×(2-5i) | (5+4i)-(-3+4i) | (2+3i)/(2-3i) | |
| (-4+3i)+(4-3i) | (3+5i)×(2+3i) | (4+2i)-(-1+2i) | (5-4i)/(-3+2i) | |
| (-2+5i)+(2-5i) | (3-4i)×(-7+3i) | (7-2i)-(-4+3i) | (-5+2i)/(6-7i) | |
| (3-4i)+(-3+4i) | (6+7i)×(-5+2i) | (-9+4i)-(3+5i) | (1+8i)/(-3+i) | |
| (7-2i)+(-7+3i) | (1+8i)×(-9+4i) | (2+3i)-(-3+i) | (-8+i)/(7-2i) | |
| (-5+2i)+(5-2i) | (3+4i)×(-8+i) | (-3+4i)-(6+7i) | (6-7i)/(-1+2i) | |
| (-6+7i)+(6-7i) | (7-2i)×(-3+i) | (3+5i)-(-9+4i) | (3+4i)/(-5+2i) | |
| (1+8i)+(-8+i) | (2+3i)×(6-7i) | (-5+2i)-(3+4i) | (-9+4i)/(5-7i) | |
| (-9+4i)+(9-4i) | (-5+2i)×(7-2i) | (-4+3i)-(2+3i) | (6+7i)/(1+8i) | |
| (8-5i)+(-8+5i) | (-1+2i)×(6+7i) | (7-5i)-(-8+i) | (3+5i)/(-4+3i) | |
Решить задачу
| Номер варианта | Задание: |
| В партии из 8 деталей имеется 6 стандартных. Найти вероятность того, что среди пяти взятых наугад деталей ровно три стандартных. | |
| В цехе работают 6 мужчин и 4 женщины. По табельным номерам наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц окажутся 3 женщины. | |
| В группе 12 студентов, среди которых 8 отличников. По списку отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов пять отличников. | |
| В урне 5 белых и 4 черных шаров. Из урны наугад вынимают 3 шара. Найти вероятность того, что среди вынутых шаров будет 2 белых. | |
| В партии из 10 деталей имеется 8 стандартных. Найти вероятность того, что среди 6 взятых наугад деталей ровно 4 стандартных. | |
| В группе 16 студентов, среди которых 10 отличников. По списку отобраны 12 студентов. Найти вероятность того, что среди отобранных студентов 6 отличников | |
| В цехе работают 7 мужчин и 5 женщин. По табельным номерам наудачу отобраны семь8 человек. Найти вероятность того, что среди отобранных лиц окажутся 4 женщины. | |
| В урне 7 белых и 5 черных шаров. Из урны наугад вынимают 6 шаров. Найти вероятность того, что среди вынутых шаров будет 4 белых. | |
| В партии из 12 деталей имеется 8 стандартных. Найти вероятность того, что среди 7 взятых наугад деталей ровно 5 стандартных. | |
| В группе 14 студентов, среди которых 9 отличников. По списку отобраны 11 студентов. Найти вероятность того, что среди отобранных студентов 5 отличников |

Пример 2. Выполнить действия над матрицами 
Составить матрицу М=(2А – В)(В+Е)
Решение
Составим матрицу 2А – В, для чего все элементы матрицы А умножим на 2, а затем из каждого элемента матрицы 2А вычтем соответствующий элемент матрицы В.

Составим матрицу В+Е, где матрица Е является единичной матрицей третьего порядка:
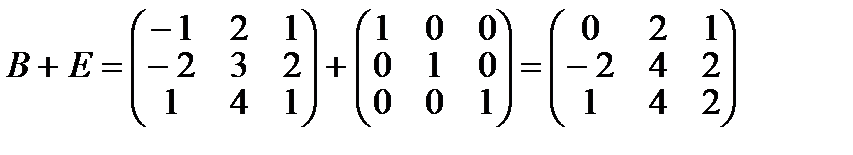
Матрица М является произведением полученных матриц, то-есть каждый ее элемент равен сумме произведений соответствующих элементов строки матрицы 2А-В и столбца матрицы В+Е
 Пример 3. Вычислить определитель матрицы:
Пример 3. Вычислить определитель матрицы:
а) 
Решение
а) Для вычисления определителя второго порядка воспользуемся правилом, изложенным в учебной литературе:

б) Для вычисления определителя третьего порядка воспользуемся одним из правил, называемым разложением по элементам первой строки:
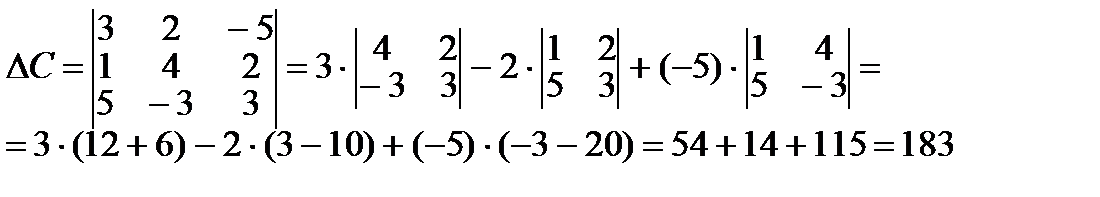
Пример 4. Решить систему уравнений по формулам Крамера 
Решение
Для решения задачи нужно вычислить четыре определителя третьего порядка:
· главный определитель, составленный из коэффициентов при неизвестных;
· дополнительный для х, полученный из главного определителя заменой чисел первого столбца на свободные члены;
· дополнительный для у, полученный из главного определителя заменой чисел второго столбца на свободные члены;
· дополнительный для z, полученный из главного определителя заменой чисел третьего столбца на свободные члены;

Для получения значений неизвестных требуется разделить значения дополнительных определителей на главный определитель.

Решение задачи можно проверить при помощи найденных значений в уравнения системы.
Пример 5. Вычислить пределы функций:




Пример 6.
а) Найти площадь фигуры, ограниченной линиями: у=1 – х2 + 4х и 2х – у – 2 =0
Для определения точек пересечения линий составим уравнение из равенства выражений этих линий: 1 – х2 + 4х = 2х – 2; получим уравнение: х2 – 2х – 3 = 0.
Корнями этого уравнения являются числа: (-1) и 3. Для построения линий найдем значения функций и составим их таблицы:
| х | -1 | х | -1 | ||||||
| у1 | -4 | у2 | -4 |
Построив фигуру на плоскости, вычислим ее площадь, определив значение интеграла