Определение взаимного положения прямой и плоскости - позиционная задача, для решения которой применяется метод вспомогательных секущих плоскостей. Сущность метода заключается в следующем:
через прямую проведем вспомогательную секущую плоскость g и установим относительное положение двух прямых а и в, последняя из которых является линией пересечения вспомогательной секущей плоскости g и данной плоскости a(рис.5.13).

Рисунок 5.13. Метод вспомогательных секущих плоскостей
Каждому из трех возможных случаев относительного расположения этих прямых соответствует аналогичный случай взаимного расположения прямой и плоскости. Так, если обе прямые совпадают, то прямая а лежит в плоскости a, параллельность прямых укажет на параллельность прямой и плоскости и, наконец, пересечение прямых соответствует случаю когда прямая а пересекает плоскость a.
Таким образом возможны три случая относительного расположения прямой и плоскости:
· Прямая принадлежит плоскости;
· Прямая параллельна плоскости;
· Прямая пересекает плоскость, частный случай – прямая перпендикулярна плоскости.
Рассмотрим каждый случай.
Прямая линия, принадлежащая плоскости
Аксиома 1. Прямая принадлежит плоскости, если две её точки принадлежат той же плоскости
Аксиома 2. Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости
Главные линии в плоскости
Среди прямых линий, принадлежащих плоскости, особое место занимают прямые, занимающие частное положение в пространстве:
1. Горизонтали h - прямые, лежащие в данной плоскости и параллельные горизонтальной плоскости проекций (hÎАВС, h//P1, h2//Ох,h3//Оy)(рис.5.16).

А) модель

Б) эпюр
Рисунок 5.16. Горизонталь
2. Фронтали f - прямые, расположенные в плоскости и параллельные фронтальной плоскости проекций (fÎАВС, f//P2, f1//Ох, f3//Оz)(рис.5.17).
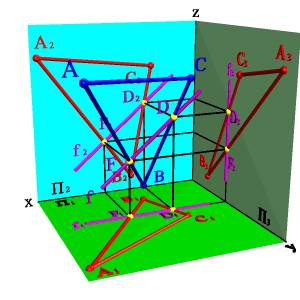
А) модель
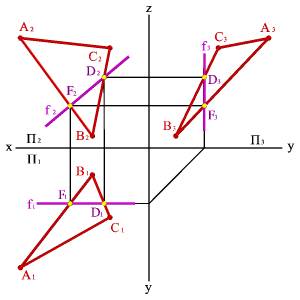
Б) эпюр
Рисунок 5.17. Фронталь
3. Профильные прямые р - прямые, которые находятся в данной плоскости и параллельны профильной плоскости проекций (рÎАВС, р//P3, р1^Ох, р2^Ох) (рис.5.18).

А) модель

Б) эпюр
Рисунок 5.18. Профильная прямая
Следует заметить, что следы плоскости можно отнести тоже к главным линиям. Горизонтальный след - это горизонталь плоскости, фронтальный - фронталь и профильный - профильная линия плоскости.
4. Линия наибольшего ската и её горизонтальная проекция образуют линейный угол j, которым измеряется двугранный угол, составленный данной плоскостью и горизонтальной плоскостью проекций (рис.5.19).

А) модель

Б) эпюр
Рисунок 5.19. Линия наибольшего ската
Очевидно, что если прямая не имеет двух общих точек с плоскостью, то она или параллельна плоскости, или пересекает ее.






