Комплексные числа. Арифметические действия с ними.
Виет, который занимался решениями квадратных уравнений и их свойствами придумал символ, который помог различать уравнения, в «старом» смысле не имеют решений. Для этого он взял букву i (мнимый) наделил его свойством и обозвал мнимая единица.
ii=  = -1
|
“Решение” уравнения:
1) 
можно записать так 
2) 
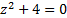можно записать так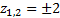 
Числа подобного вида, т.е. вида a+bi, где a и b обычные действительные, вещественные числа, а i определенная выше мнимая единица. Принято называть комплексные (составные) или мнимыми числами a-действительное, а bi-чисто мнимые
(-2+/-3i) 
+4(-2+/-3i)+13=4+(-/+12i)+(-9)-8+/-12i+13=0+0i=0
Арифметические действия
с комплексными числами осуществляются так, будто бы они обычным образом осуществляются с двучленами.
Деление таких чисел производится так, будто бы избавляетесь от i(как от корня) в знаменателе
Тригонометрическая и показательная формы комплексного числа
Так как, любое комплексное число фактически определяется двумя действительными (как координаты точки или вектора), то их принято обозначать на обычной, вещественной, координированной плоскости
При этом действительную часть принято считать абсциссой этой точки, а коэффициент при i мнимой части принято считать ординаты этой же точки.
!При этом ось абсцисс будем называть реальной осью, а ось ординат - мнимой осью!
Но чаще мы будем считать изображением компл.числа соответствующей радиусу вектора. Отсюда следует, что точка (0;1) является изображением числа i.
Следует, 1) Понятие“ 
” для компл. чисел не имеет смысла 2) для них(для чисел) можно(как и для векторов) ввести понятие длина-модуль 
! Будем называть аргументом комплексного числа любой угол на который отклоняется от полож. полуоси абсцисс радиус векторов, который является изображением данного комплексного числа.
При этом главным считается тот, который удовлетворяет неравенство
Обозначают обычно его arg z или 
Из определения 
и 
как отношений в прям треугол. 
, 
А значит, число тригонометрическая формула
–Алгебраическая форма.
Формула Эйлера 1.
2. 
Показательная формула
Из формулы Эйлера следует
Возведение в натуральную степень и извлечение корня из комплексных чисел
Свойства степеней
Из определения алгебраического корня n-степени из любого числа z как любого числа w, которая в n-степени превращается в z, те является решением уравнения
=z
Можно показать, что таких корней существует ровно n штук и все они могут быть найдены по формуле:
Линейные действия с матрицами
Матрицей принято называть таблицу, элементами которой, могут быть как числа, так функции, векторы и даже матрицы.
При этом матрицей размерами m*n называется таблица, состоящая из m строк,n-столбцов. Обозначать матрицы принято заглавными буквами любого алфавита, а их элементы(матрицы) соответствующими малыми буквами тго же алфавита где первый нижний индекс i указывает n строчки, а второй j n столбика. Изображают матрицы:
Действия с матрицами:
Транспонирование. 2 матрицы называются взаимно транспонированными, если строки любой из них являются соответствующими строчками(по номеру) другой из них, а обозначать такие взаимно-транспонированные матрицы принято одной и той же буквой приписывыя одной из них верхний индекс Т.
Сложение- сумма 2х и более матриц одинаковых размеров.
А и В называется новая матрица тех размеров С для которых
Умножение матриц
Произведением любой матрицы на число (лямбда) будет матрица тех же размеров, все элементы которой умноженное на это число
Последние 2 действия принято называть линейными действиями с матрицами, а выражение «лямбдаА+лВ» такого вида называют линейной комбинацией
Будем называть произведение матрицы строки (S) на матрицу столбик
Матрицами размером 1*1 единственный элемент которой будет
Произведением Матрицы А размерами m*n на матрицу В n*p называется С m*p элементами которой являются произведения соответствующей строчки А на столбик матрицы В, те.
Пример
Замечание: Очевидно, что такое умножение матриц не обладает свойством перестановочности, тк В*А может не существовать, а если оно и существует, то А*В не равно (=/) В*А
Однако имеет место быть:
Делить матрицы нельзя!
