Діагностична контрольна робота з геометрії
У 9-х класах
Контрольна робота містить 20 варіантів. Кожен із них складається з трьох частин, які відрізняються складністю та формою тестових завдань.
У І частині контрольної роботи запропоновано п’ять завдань з вибором однієї правильної відповіді, що відповідають початковому та середньому рівням навчальних досягнень учнів. До кожного завдання подано чотири варіанти відповіді, з яких тільки одна правильна. Завдання вважається виконаним правильно, якщо учень записав тільки літеру, якою позначено правильний варіант відповіді. Правильна відповідь за кожне із п’яти завдань оцінюється одним балом.
ІІ частина контрольної роботи складається з двох завдань, що відповідають достатньому рівню навчальних досягнень учнів. Розв’язання повинно мати короткий запис без обґрунтування. Правильне розв’язання кожного із завдань цього блоку оцінюється двома балами.
ІІІ частина контрольної роботи складається з одного завдання, що відповідає високому рівню навчальних досягнень учнів, розв’язання якого повинно мати розгорнутий запис з обґрунтуванням. Правильне розв’язання завдання оцінюється трьома балами.
Сума балів нараховується за правильно виконані учнем завдання відповідно максимально можливій кількості запропонованих балів для кожної частини (5; 4; 3–всього 12балів).
Контрольна робота розрахована на 45 хвилин. Роботи виконуються у зошитах або на окремих аркушах. При виконанні роботи необхідно вказати номер завдання. Текст завдань переписувати не обов’язково.
Примітка. У тексти завдань можна вносити корективи: збільшити (зменшити) кількість завдань або посилити (послабити) ступінь складності.
Зразок підпису роботи
Діагностична контрольна робота
геометрії
учня (учениці) 9_____ класу
______________________________
назва навчального закладу
______________________________
прізвище ім’я в родовому відмінку
Варіант _____
Звіт з математики
Місто (район)_________________________________________
Табл.1. Кількісний звіт
| Кількість учнів | Писало | Результати | |||||||
| І рівня | ІІ рівня | ІІІ рівня | ІV рівня | ||||||
| кількість | % | кількість | % | кількість | % | кількість | % | ||
Табл.2. Якісний звіт
| Всього учнів | Писало | Правильна відповідь завдань у % | Кількість набраних балів у % | Кількість набраних балів у % | Кількість набраних балів у % | ||||||||||||
| Кількість учнів | % | 6 завдання | 7 завдання | 8 завдання | |||||||||||||
Аналітичний звіт: матеріал, засвоєний учнями якісно; допущені типові помилки, причини та шляхи їх подолання.
Примітка. Якщо до тексту завдань були внесені корективи, то необхідно надіслати змінені тексти з обґрунтуванням необхідності такого кроку.
Виконавець підпис прізвище, ініціали
Варіант 1
I частина (5 балів)
Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.
1. Знайдіть кути даного паралелограма.
А) 65°, 65°,115°, 115°; Б) 80°, 80°, 100°, 100°;
В) 120°, 120°, 60°, 60°; Г) 40°, 40°, 40°, 40°.
2. Сторони трикутника дорівнюють 8 см, 10 см, 12 см. Знайдіть сторони трикутника, вершинами якого є середини сторін даного трикутника.
А) 16 см, 20 см, 24 см; Б) 4 см, 5 см, 6 см;
В) 2 см, 2,5 см, 3 см; Г) 10 см, 12 см, 14 см.
3. Висота рівнобедреного трикутника дорівнює 15 см, а основа – 16 см. Знайдіть бічну сторону трикутника.
А) 34 см; Б) 17 см;
В) 31 см; Г) 23 см.
4. Точка О – центр кола,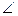 
В =500. Знайдіть градусну міру 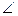АОС?
А) 960; Б) 480;
В) 240; Г) 1000.
5. Чи подібні трикутники АВС і А1В1С1, якщо АВ = 20 см, АС = 40 см, ВС = 30 см, А1В1 = 10 см, А1С1 = 20 см, В1С1 = 15 см?
А) так; Б) ні; В) встановити не можна.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.
6. Периметр паралелограма дорівнює 244 см. Одна із його сторін більша від другої на 50 см. Знайдіть довжини сторін паралелограма.
7. Розв’яжіть прямокутний трикутник АВС (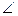 С=900) за відомими елементами: АВ = 8 см, АС = 5 см.
ІІІ частина (3 бали)
Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.
8. В трикутнику одна із сторін 29 см, а інша ділиться точкою дотику вписаного в трикутник кола на відрізки 24 см та 1 см, починаючи від кінця першої сторони. Знайдіть площу трикутника.
Варіант 2
I частина (5 балів)
Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.
1. Знайдіть кути даного паралелограма.
А) 40°, 40°, 140°, 140°; Б) 60°, 60°, 120°, 120°;
В) 20°, 20°, 160°, 160°; Г) 60°, 60°, 60°, 60°.
2. Сторони трикутника дорівнюють 12 см, 14 см, та 18 см. Знайдіть периметр трикутника, вершинами якого є середини сторін даного трикутника.
А) 44 см; Б) 88 см;
В) 22 см; Г) 11 см.
3. Бічна сторона рівнобедреного трикутника дорівнює 29 см, а висота, проведена до основи, дорівнює 21 см. Чому дорівнює основа трикутника?
А) 50 см; Б) 8 см;
В) 40 см; Г) 25 см.
4. Точка О – центр кола, зображеного на рисунку. Яка градусна міра 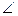СDE?
А) 32°; Б) 43°;
В) 26°; Г) 16°.
5. Трикутники АВС і А1В1С1 подібні. АС = 8 см, А1В1 = 12 см, і В1С1 = 14 см, А1С1 = 16 см. Знайдіть сторони АВ і ВС.
А) АВ=7 см, ВС=6 см; Б) АВ=6 см, ВС=7 см;
В) АВ=24 см, ВС=28 см; Г) АВ=4 см, ВС=6 см.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.
6. Периметр паралелограма дорівнює 299,2 дм. Одна сторона довша за другу на 20%. Обчисліть усі сторони паралелограма.
7. Розв’яжіть прямокутний трикутник АВС (
) за відомими елементами: АВ = 12 см, 
.
ІІІ частина (3 бали)
Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.
В трикутнику, периметр якого 60 см, одна із сторін ділиться точкою дотику вписаного в трикутник кола на відрізки 24 см та 5 см. Знайдіть площу трикутника. Варіант 3
I частина (5 балів)
Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.
1. 
Знайдіть за рисунком кути паралелограма АВСD.
А) 105°, 75°, 105°, 75°; Б) 110°, 70°, 110°, 70°;
В) 135°, 135°, 135°, 135°; Г) 130°, 50°, 130°, 50°.
2. Знайдіть середню лінію трапеції, якщо її основи дорівнюють 5 см та 7 см.
А) 6 см; Б) 12 см;
В) 2 см; Г) 24 см.
3. Площа прямокутника дорівнює 48 см2, одна з його сторін 6 см. Знайдіть периметр прямокутника.
А) 30 см; Б) 56 см;
В) 28см; Г) 14 см.
4. Яка градусна міра ВАD чотирикутника АВСD, зображеного на рисунку?
А) 52°; Б) 72°;
В) 80°; Г) 76°.
5. В рівнобедреному трикутнику АВС з основою АС, 
А=0,6, АВ = 10 см. Знайдіть висоту, проведену до основи.
А) 10 см; Б) 8 см;
В) 6 см; Г) 3 см.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.
6. З однієї точки до даної прямої проведені перпендикуляр і дві похилі. Знайдіть довжину перпендикуляра, якщо похилі дорівнюють 41 см і 50 см, а їхні проекції на дану пряму відносяться, як 3: 10.
7. Знайдіть дві сторони трикутника, якщо їх сума дорівнює 72 см, а бісектриса кута між ними ділить третю сторону у відношенні 3: 5.
ІІІ частина (3 бали)
Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.
8. З точки В до прямої a проведені дві похилі: ВА = 20 см і ВС = 13 см. Проекція похилої ВА більше проекції похилої ВС на 11 см. Знайдіть проекції цих похилих.
Варіант 4
I частина (5 балів)
Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.
1. Знайдіть за рисунком кути паралелограма АВСD.
А) 35°, 145°, 35°, 145°; Б) 55°, 125°, 55°, 125°;
В) 45°, 135°, 45°, 135°; Г) 65°, 115°, 65°, 115°.
2. Основи трапеції дорівнюють 14 дм і 10 дм. Знайдіть середню лінію трапеції.
А) 4 дм; Б) 24 дм;
В) 12 дм; Г) 48 дм.
3. Периметр прямокутника 30 см, одна з його сторін 9 см. Знайдіть площу прямокутника.
А) 48 см2; Б) 54 см2;
В) 64 см2; Г) 45 см2.
4. 
Чому дорівнює градусна міра АDС, чотирикутника АВСD, зображеного на рисунку?
А) 28°; Б) 62°;
В) 116°; Г) 128°.
5. В рівнобедреному трикутнику АВС з основою АВ 
, а бічна сторона дорівнює 20 см. Знайдіть АВ.
А) 32 см; Б) 30 см;
В) 12 см; Г) 16 см.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.
6. З однієї точки до даної прямої проведені перпендикуляр і дві похилі. Знайдіть довжину перпендикуляра, якщо довжини похилих відносяться, як 10: 17, а їх проекції на дану пряму дорівнюють 12 см і 30 см.
7. Знайдіть дві сторони трикутника, якщо їх різниця дорівнює 33 см, а бісектриса кута між ними ділить третю сторону у відношенні 2: 5.
ІІІ частина (3 бали)
Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.
8. З точки А до прямої b проведено дві похилі: АС = 20 см і АВ = 13 см. Сума проекцій цих похилих дорівнює 21 см. Знайдіть проекції похилих.
Варіант 5
I частина (5 балів)
Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.
1. В колі проведені радіуси OM і ON. Знайдіть градусну міру дуги MN, якщо відповідний їй центральний кут дорівнює 120°.
А) 60°; Б) 240°;
В) 120°; Г) 180°.
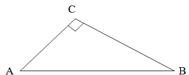2. В прямокутному трикутнику АВС, АВ = 4 см, АС = 
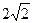см. Знайдіть 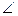АВС.
А) 60°; Б) 30°;
В) 45°; Г) 90°.
3. Менша основа трапеції дорівнює 
її більшої основи. Знайдіть середню лінію трапеції, якщо її більша основа дорівнює 12 см.
А) 10 см; Б) 8 см;
В) 6 см; Г) 4 см.
4. Точки М і Р лежать відповідно на сторонах АВ і ВС трикутника АВС, причому МР || АС. Знайдіть довжину сторони АС, якщо РС = 4 см, ВС = 12 см, МР = 6 см.
А) 
см; Б) 4 см;
В) 12 см; Г) 9 см.
5. Діагональ прямокутника дорівнює 10 см, а одна з його сторін 8 см. Знайдіть периметр прямокутника.
А) 28 см; Б) 20 см;
В) 40 см; Г) 36 см.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.
6. Кути, які утворені діагоналями ромба з однією з його сторін, відносяться як 4: 5. Знайдіть ці кути.
7. Діагональ вписаного в коло прямокутника утворює з його стороною кут 24°. Знайдіть, на які частини поділяється коло вершинами цього прямокутника.
ІІІ частина (3 бали)
Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.
