Кривые поверхности широко применяются в различных областях науки и техники при создании очертаний различных технических форм или как объекты инженерных исследований. Существуют три способа задания кривых поверхностей:
- 1. Аналитический - при помощи уравнений;
- 2. При помощи каркаса;
- 3. Кинематический, т. е. перемещением линий в пространстве.

| Рис. 7.1. Пример поверхности, заданной аналитически |
Составлением уравнений поверхностей занимается аналитическая геометрия; она рассматривает кривую поверхность как множество точек, координаты которых удовлетворяют некоторому уравнению. На рис. 7.1 приведен пример поверхности, заданной аналитически (системой алгебраических уравнений).
При каркасном способе задания кривая поверхность задается совокупностью некоторого количества линий, принадлежащих поверхности.
Каркас поверхности
Другим способом образования поверхности и ее изображения на чертеже может служить каркас поверхности.
Каркасом поверхности принято называть упорядоченное множество точек или линий, принадлежащих поверхности.
В зависимости от того, чем задается каркас поверхности, точками или линиями, каркасы называют точечными или линейными. Линейным каркасом называется множество таких линий, которые имеют единый закон образования и связаны между собой определенной зависимостью. Условия связи между линиями каркаса называются зависимостью каркаса. Эта зависимость характеризуется некоторой изменяющейся величиной, которая называется параметром каркаса. Если параметр линейного каркаса является непрерывной функцией, то каркас называется непрерывным, а если параметр - прерывная функция, то каркас называется дискретным.
На рис. 7.2 приведен пример каркаса поверхности, состоящей из двух ортогонально расположенных семейств линий а1, а2, а3,..., аn, b1, b2, b3,...bn.

Рис. 7.2. Пример линейного каркаса поверхности
Определитель поверхности
Кинематический способ образования поверхности можно представить как множество положений движущейся линии или поверхности.
Этот способ дает возможность сформулировать понятие определителя поверхности. Под этим понятием обычно подразумевают необходимую и достаточную совокупность геометрических фигур и кинематических связей между ними, которые однозначно определяют поверхность.
Определитель поверхности состоит из двух частей:
Геометрической части - совокупности геометрических фигур, с помощью которых можно образовать поверхность.
Алгоритмической части - алгоритма формирования поверхности при помощи фигур, входящих в геометрическую часть определителя.
Чтобы найти определитель поверхности, следует исходить из кинематического способа образования поверхности.
Для того чтобы построить чертеж поверхности, необходимо предварительно выявить ее определитель. Определитель поверхности выявляется путем анализа способов образования поверхности или ее основных свойств. В общем случае поверхность может быть образована несколькими способами и поэтому может иметь несколько определителей. Обычно из всех способов образования поверхности выбирают простейший.
Поверхность на чертеже задают проекциями геометрической части ее определителя. Определитель кривой поверхности Ф может быть записан в символической форме: Ф (Г) [А], где (Г) - геометрическая часть, [А] - алгоритмическая часть. Для каждой поверхности обе части определителя имеют вполне конкретное содержание.
Поверхность считается заданной на комплексном чертеже, если относительно любой точки пространства, заданной на чертеже, можно однозначно решить вопрос о принадлежности ее данной поверхности. Построение проекций любых точек и линий, принадлежащих поверхности, а также второй их проекции, если одна задана, выполняется на основании ее определителя.
Точка принадлежит поверхности, если она принадлежит линии, принадлежащей поверхности.
Рассмотрим примеры выявления определителя для некоторых простейших поверхностей:
Через три точки А, В, С, не принадлежащие одной прямой, можно провести одну и только одну плоскость (на рис. 7.3, а). Точки А, В и С составляют геометрическую часть определителя плоскости.
Вторая часть определителя, т. е. алгоритм построения в плоскости (А, В, С) любых линий и точек, выражается рассмотренными ранее условиями принадлежности прямой и точки плоскости.
На чертеже (рис. 7.3, б) плоскость задана проекциями геометрической части своего определителя: А(А1А2), В(В1В2), С(С1С2).
Цилиндрическая поверхность вращения может быть образована вращением прямой 1 || i вокруг оси i (рис. 7.4, а).

а б
Рис.7.3. Примеры определителя:
а - алгоритмическая часть; б - геометрическая часть
Геометрическая часть определителя поверхности состоит из образующей 1 и оси i. Алгоритмическая часть определителя состоит из операции вращения образующей линии 1 вокруг оси i.
Определитель цилиндрической поверхности вращения имеет вид Ф(l i, i) [А]. На чертеже (рис. 7.4, б) цилиндр вращения задан проекциями геометрической части своего определителя.
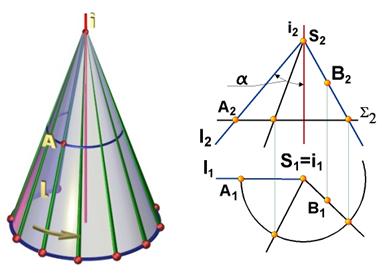
Коническая поверхность вращения может быть образована вращением прямой l, пересекающей ось вращения i под некоторым углом (рис. 7.5, а). Алгоритмическая часть определителя состоит из словесного указания о том, что поверхность образуется вращением образующей l вокруг оси i.
Определитель конической поверхности вращения имеет вид Ф(l ∩ i)[A].
На чертеже (рис. 7.5, б) конус вращения задан проекциями геометрической части его определителя:
l(l1l2) Λ i(i1i2}

а б
Рис. 7.4. Определитель цилиндрической поверхности:
а - поверхность образована вращением прямой l i вокруг оси i;
б - цилиндр вращения задан проекциями геометрической части
своего определителя
В указанных примерах определитель поверхности выявляется путем анализа способов ее образования. Рассмотрим пример выявления определителя поверхности путем анализа ее основных свойств. Возьмем, например, сферу. Сферой называется поверхность, образованная множеством точек пространства, находящихся на расстоянии | r | от данной точки O (рис. 7.6, а). Геометрическая часть определителя сферы состоит из точки O (центра сферы) и точки М, принадлежащей ее поверхности. Алгоритм построения любой точки сферы заключается в проведении через точку О произвольной прямой и откладывания на ней от точки О отрезка | OM' = | ОМ | = | r |. Определитель сферы имеет вид Ф(О, М) [А]. На рис. 7.6, б (справа) сфера задана проекциями точек О(O1O2) и М(М1М2), которые составляют геометрическую часть ее определителя, и показано построение произвольной точки Мn(Мn1 Мn2) сферы. При чтении чертежа немаловажную роль играет его наглядность. Задание поверхности проекциями геометрической части ее определителя не обеспечивает наглядности изображений. Поэтому для придания чертежу поверхности большей наглядности и выразительности прибегают к построению очерков ее проекций или проекций достаточно плотного каркаса ее образующих.
а б
Рис. 7.5. Изображение определителя конической поверхности:
а - алгоритмическая часть; б - геометрическая часть
При проецировании поверхности на какую-либо плоскость проекций часть проецирующих лучей касается ее, образуя проецирующую поверхность. Точки касания при этом образуют линию видимого контура поверхности относительно этой плоскости проекций (рис. 7.7). Очерк проекции поверхности является проекцией соответствующей линии видимого контура. Линия видимого контура поверхности разделяет ее на две части - видимую, обращенную к наблюдателю, и невидимую. Никакая точка поверхности не может спроецироваться за пределы очерка.
На чертежах (рис. 7.8, а, в) конус вращения и сфера заданы проекциями геометрической части своего определителя, а на чертежах (рис. 7.8, б, г) для тех же поверхностей построены очерки их проекций. Последние, безусловно, обладают большей наглядностью и выразительностью.
Кривые поверхности разделяются на линейчатые и нелинейчатые, закономерные и незакономерные. Поверхность называется линейчатой, если она может быть образована перемещением прямой линии, в противном случае - нелинейчатой.

Рис. 7.6. Изображение определителя сферы:
а - алгоритмическая часть; б - геометрическая часть
Если поверхность может быть задана каким-либо уравнением, она называется закономерной, в противном случае - незакономерной, или графической (задается только чертежом).
Закономерные поверхности, в зависимости от вида уравнения, разделяются на алгебраические и трансцендентные.
Алгебраическое уравнение n-й степени (в декартовых координатах) задает алгебраическую поверхность n-го порядка (трансцендентные поверхности порядка не имеют). Алгебраическая поверхность n-го порядка пересекается плоскостью по кривой n-го порядка, а с прямой линией - в n точках.
Плоскость, имеющую уравнение первой степени (с произвольной плоскостью пересекается по прямой линии, а с прямой - в одной точке), можно рассматривать как поверхность первого порядка. Примерами кривых поверхностей второго порядка могут служить поверхности, образованные вращением кривых второго порядка вокруг одной из своих осей.
Поверхности второго порядка пересекаются с произвольной плоскостью по кривым второго порядка, а с прямой - в двух точках. Примером поверхности четвертого порядка может служить тор (см. поверхности вращения).

Рис. 7.7. Образование проекций сферы
Определитель может быть положен в основу классификации поверхностей. К одному и тому же классу относятся поверхности, имеющие одинаковую структуру определителя.
Наибольшее применение в технике получили кинематические кривые поверхности с образующими постоянной формы:
1. Линейчатые поверхности:
а) развертывающиеся;
б) неразвертывающиеся;
В) винтовые.
Поверхности вращения.
7.2. Линейчатые поверхности
Как уже отмечалось, поверхность называется линейчатой, если она может быть образована перемещением прямой линии. Поверхность, которая не может быть образована движением прямой линии, называется нелинейчатой. Например, конус вращения - линейчатая поверхность, а сфера - нелинейчатая. Через любую точку линейчатой поверхности можно провести, по крайней мере, одну прямую, целиком принадлежащую поверхности. Множество таких прямых представляет собой непрерывный каркас линейчатой поверхности. Линейчатые поверхности разделяются на два вида:

Рис. 7.8. а, в - проекции геометрической части определителей конуса и сферы; б, г - очерки проекций конуса и сферы






