1. Методы проецирования начертательной геометрии
1.1. Предмет начертательной геометрии
1.2. Из истории начертательной геометрии
1.3. Способы проецирования
1.4. Инвариантные свойства параллельного проецирования
1.5. Ортогональное проецирование
1.6. Система трех плоскостей проекций. Эпюр Монжа
2. Точка, прямая и плоскость на комплексном чертеже
2.1.Способы задания точки и прямой на комплексном чертеже
2.2. Свойства прямой на комплексном чертеже
2.3. Частные положения прямой в пространстве
2.4. Следы прямой линии
2.5. Плоскость. Способы задания плоскости на комплексном чертеже
2.6. Общее и частные положения плоскости в пространстве
2.7. Следы плоскости
3. Взаимное расположение геометрических элементов. Основные позиционные задачи
3.1. Определение позиционных задач
3.2. Метод конкурирующих точек
3.3. Прямая и точка
3.4. Взаимные положения прямых
3.5. Прямая и точка на плоскости
3.6. Взаимное положение прямой и плоскости
3.7. Пересечение прямой и плоскости
4. Перпендикулярность прямых и плоскостей. Метрические задачи
4.1.Условие перпендикулярности двух прямых на комплексном чертеже
4.2. Условие перпендикулярности прямой и плоскости
4. 3. Условие перпендикулярности двух плоскостей
4.4. Определение длины отрезка и углов его наклона к плоскостям проекций
4.5. Линии наибольшего наклона (ската)
5. Способы преобразования комплексного чертежа
5.1. Необходимость преобразований комплексного чертежа
5.2. Задачи на преобразование комплексного чертежа
6. Метрические задачи
6.1. Общие положения
6.2. Задачи на определение расстояний между геометрическими фигурами
6.3. Задачи на определение действительных величин плоских геометрических фигур и углов между ними
7. Поверхности
7.1. Понятия и определения
7.2. Линейчатые поверхности
7.3. Неразвертывающиеся (косые) линейчатые поверхности
8. Позиционные задачи на поверхности
8.1. Пересечение поверхности плоскостью
8.2. Конические сечения
8.3. Взаимные пересечения поверхностей
9. Построение разверток
9.1. Основные понятия и свойства
9.2. Построение разверток многогранников
9.3. Построение разверток кривых развертывающихся поверхностей
9.4. Построение условных разверток неразвертывающихся поверхностей
1.3. Способы проецирования
Проекцией точки А на плоскость проекций p1 называется точка А1пересечения проецирующей прямой ℓ с плоскостью проекций p 1, проходящей через точку А (рис. 1.1):
Проекция любой геометрической фигуры есть множество проекций всех ее точек. Направление проецирующих прямых ℓ и положение плоскостей p1определяют аппарат проецирования.
Центральным проецированием называется такое проецирование, при котором все проецирующие лучи исходят из одной точки S - центра проецирования (рис. 1.2).
Параллельным проецированием называют такое проецирование, при котором все проецирующие прямые параллельны заданному направлению S
(рис. 1.3).
Параллельное проецирование представляет собой частный случай центрального проецирования, когда точка S находится на бесконечно большом расстоянии от плоскости проекций p1.
При заданном аппарате проецирования каждой точке пространства соответствует одна и только одна точка на плоскости проекций.
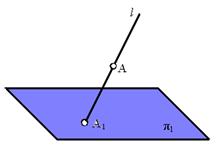
Рис. 1.1. Проекция точки А а плоскость проекций π 1
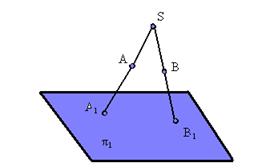
| Рис. 1.2. Пример центральногопроецирования |

Одна проекция точки не определяет положения этой точки в пространстве. Действительно, проекции А1 может соответствовать бесчисленное множество точек А', А'',..., расположенных на проецирующей прямой ℓ (рис. 1.4).
Для определения положения точки в пространстве при любом аппарате проецирования необходимо иметь две ее проекции, полученных при двух различных направлениях проецирования (или при двух различных центрах проецирования).
Так, из рис. 1.5 видно, что две проекции точки А (А1 и А2), полученные при двух направлениях проецирования S1 и S2, определяют единственным образом положение самой точки А в пространстве - как пересечение проецирующих прямых ℓ1 и ℓ2, проведенных из проекций А1 и А2 параллельно направлениям проецирования S1 и S2.


Рис. 1.5. Определение положения точки А в пространстве
1.4. Инвариантные свойства параллельного проецирования
Геометрические фигуры в общем случае проецируются на плоскость проекций с искажением. Проекции не сохраняют линейные и угловые величины оригинала. Характер искажений зависит от положения геометрической фигуры в пространстве, от аппарата проецирования и от положения плоскости проекций.
Однако некоторые геометрические свойства фигур остаются неизменными в процессе проецирования. Такие свойства геометрических фигур называются независимыми или инвариантными для данного аппарата проецирования.
Рассмотрим основные инвариантные свойства параллельного проецирования.
1. Проекция точки есть точка
Это очевидно из самого определения проекции как точка пересечения проецирующей прямой с плоскостью.
2. Проекция прямой есть прямая (рис. 1.6)

Рис. 1.6. Изображения инвариантных свойств 2, 3, 4
Все проецирующие прямые, проходящие через точки прямой а параллельно направлению проецирования S, образуют проецирующую, или лучевую, плоскость a.
Проекция прямой а на плоскость p1 определяется как линия пересечения этой лучевой плоскости a с плоскостью p1.
3. Если точка К принадлежит прямой а, то и проекция этой точки принадлежит проекции прямой (рис. 1.6).
Это свойство следует непосредственно из определения проекции геометрической фигуры как множества проекций всех точек.
Если точка К принадлежит прямой а и плоскости a, то и проецирующий луч lКпринадлежит плоскости a. Следовательно, этот луч пересечет плоскость p1 в линии пересечения плоскостей a и p1, т. е. в точке К1, принадлежащей проекции прямой а1.
4. Если точка К делит отрезок АD в отношении m: n то и проекция этой точки делит в таком же отношении проекцию этого отрезка (рис. 1.6):
Фигура ADD1A1 - трапеция. Прямая КК1 параллельна основаниям трапеции АА1 и DD1, следовательно делит ее стороны АD и А1D1 на пропорциональные части.
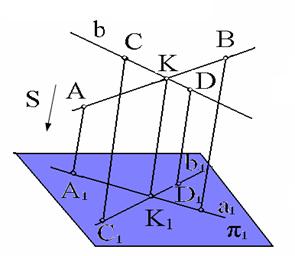
5. Проекция точки пересечения прямых есть точка пересечения проекций этих прямых (рис. 1.7)
a
|
Рис. 1.7. Пример инвариантного свойства 5
Действительно, точка К принадлежит одновременно отрезкам АВ и CD прямых а и b. По третьему инвариантному свойству проекция этой точки К1должна принадлежать проекциям этих прямых, т.е. должна являться точкой пересечения этих проекций.
6. Проекции параллельных прямых параллельны (рис. 1.8)
Лучевые плоскости a и b, проходят через параллельные прямые АВ и CD. Они параллельны, так как две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости (АВ½÷ CD и АА1÷÷ СС1). Но две параллельные плоскости пересекаются с третьей по параллельным прямым, следовательно, А1В1÷÷ С1D1.
7. Плоский многоугольник в общем случае проецируется в многоугольник с тем же числом вершин.
Исключение составляет многоугольник (плоская ломаная или кривая линия) расположенный в проецирующей (лучевой) плоскости. Такой многоугольник проецируется в прямую линию (рис. 1. 9).
8. Прямая, параллельная направлению проецирования, проецируется в точку (рис. 1.9)
9. Проекция плоской фигуры, параллельной плоскости проекций, конгруэнтна этой фигуре (рис. 1.10).
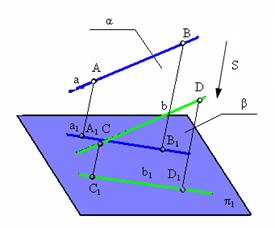
Рис. 1.8. Пример инвариантного свойства 6

Рис. 1. 9. Примеры инвариантных свойств 7, 8
Следствия этого инвариантного свойства следующие:
1. Проекция отрезка прямой, параллельной плоскости проекций, конгруэнтна и параллельна самому отрезку (рис. 1.10):
2. Проекция угла, стороны которого параллельны плоскости проекций, конгруэнтна этому углу (рис. 1.10).
1.5. Ортогональное проецирование
Направление проецирования перпендикулярно (ортогонально) плоскости проекций S ^ p1 (рис. 1.11). Ортогональное проецирование является частным случаем параллельного проецирования.
Ортогональное проецирование находит широкое применение в инженерной практике для изображения геометрических фигур на плоскости, т. к. обладает рядом преимуществ перед центральным и параллельным (косоугольным) проецированием к которым можно отнести:
а) простоту графических построений для определения ортогональных проекций точек;
б) возможность при определенных условиях сохранить на проекциях форму и размеры проецируемой фигуры.
Указанные преимущества обеспечили широкое применение ортогонального проецирования в технике, в частности для составления машиностроительных чертежей.

Рис. 1.10. Пример инвариантного свойства 9
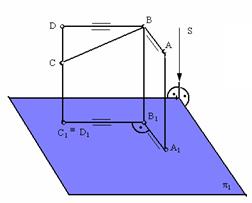
Рис. 1.11. Ортогональная проекция прямого угла
Для ортогонального проецирования справедливы все девять инвариантных свойств, рассмотренных выше. Кроме того, необходимо отметить еще одно, десятое, инвариантное свойство, которое справедливо только для ортогонального проецирования.
10. Если хотя бы одна сторона прямого угла параллельна плоскости проекций, то на эту плоскость проекций прямой угол проецируется без искажения (рис. 1.11)
На рис. 1.11 показан прямой угол АВD, обе стороны которого параллельны плоскости проекций π 1. По инвариантному свойству 9 этот угол проецируется на плоскость π 1 без искажения, т. е.  А1В1D1=90°.
А1В1D1=90°.
Возьмем на проецирующем луче DD1 произвольную точку С, тогда полученный  АВС будет прямым, т. к. АВ
АВС будет прямым, т. к. АВ  ВВ1DD1.
ВВ1DD1.
Проекцией этого прямого угла АВС, у которого только одна сторона АВ параллельна плоскости проекций π 1, будет прямой угол А1В1D1.
1.6. Система трех плоскостей проекций. Эпюр Монжа
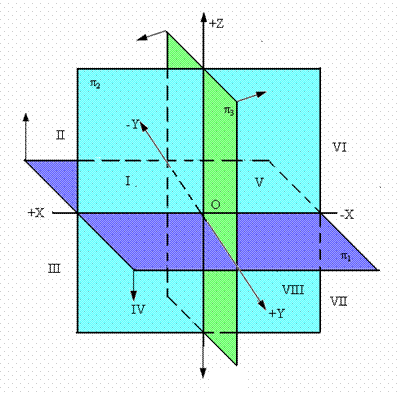
Все пространственные геометрические фигуры могут быть ориентированы относительно декартовой прямоугольной системы координатных осей - системы трех взаимно перпендикулярных координатных плоскостей (рис. 1.12).
Эти координатные плоскости обозначаются:
1. Горизонтальная плоскость проекций - π 1;
2. Фронтальная плоскость проекций - π 2;
3. Профильная плоскость проекций - π 3.
Линии пересечения этих плоскостей образуют координатные оси: ось абсцисс - Х; ось ординат - Y; ось аппликат - Z. Точка О пересечения координатных осей принимается за начало координат и обозначается буквой О. Положительными направлениями осей считают: для оси x - влево от начала координат, для оси Y - в сторону зрителя от плоскости π2, для оси z - вверх от плоскости π1; противоположные направления считают отрицательными.
 -z
-z
|
Рис. 1.12. Изображение системы трех плоскостей проекций
Для упрощения дальнейших рассуждений будем рассматривать только часть пространства, расположенную влево от профильной плоскости проекций π3.
При таком допущении три координатные плоскости проекций образуют четыре пространственных угла - октанта (в общем случае - 8 октантов).
Из рис. 1.12 видно, что ось абсцисс Х делит горизонтальную плоскость проекций π1 на две части: переднюю полу π1 (оси Х и Y) и заднюю полу π1 (оси Х и - Y).
Ось абсцисс Х делит фронтальную плоскость проекций p2 также на две части: верхнюю полу π2 (оси Х и Z) и нижнюю полу π2 (оси Х и - Z).
Оси ординат Y и аппликат Z делят профильную плоскость проекций π3 на четыре части:
- 1. Верхнюю переднюю полу π3 (оси Y и Z)
- 2. Верхнюю заднюю полу π3 (оси -Y и Z)
- 3. Нижнюю переднюю полу π3 (оси Y и -Z)
- 4. Нижнюю заднюю полу π3 (оси - Y и -Z)
Для того, чтобы получить плоскую (двухмерную) модель пространственных координатных плоскостей проекций, горизонтальную π1 и профильную p3плоскости совмещают с фронтальной π2 в том порядке как это показано стрелками на рис. 1.12.
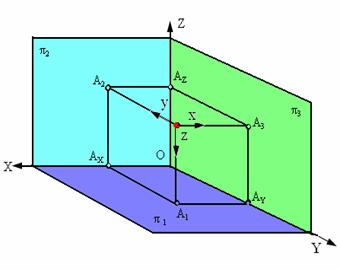
Рис. 1.13. Пространственная модель точки А
При этом горизонтальная плоскость проекций π1 вращается вокруг оси Х на 90°, а профильная плоскость проекций π3 вращается вокруг оси Z также на 90° (направление вращения показано на рис. 1.12).
Полученное таким образом совмещение трех плоскостей проекций является плоской моделью системы трех пространственных координатных плоскостей.
Для построения плоской модели пространственной геометрической фигуры каждая ее точка проецируется ортогонально на плоскости проекций π1, π2 и π3, которые затем совмещаются в одну плоскость. Полученная таким образом плоская модель пространственной геометрической фигуры называется эпюром Монжа.
Порядок построения эпюра точки, расположенной в первом октанте.
На рис. 1.13 изображена пространственная точка А, координаты которой (x, y, z) показывают величины расстояний, на которые точка удалена от плоскостей проекций.
Для того чтобы получить ортогональные проекции точки А, необходимо из этой точки опустить перпендикуляры на плоскости проекций.
Точки пересечения этих перпендикуляров с плоскостями проекций образуют проекции точки А:
А1 - горизонтальную проекцию точки;
А2 - фронтальную проекцию точки;
А3 - профильную проекцию точки.

| Рис. 1.14. Эпюр точки А |
На рис. 1.14 плоскости проекций π1 и π3 совмещены с плоскостью чертежа (с плоскостью проекции π2), а вместе с ними совмещены с плоскостью чертежа и проекции точки А (А1, А2, А3) и таким образом получена плоскостная модель координатных плоскостей проекций и плоскостная модель пространственной точки А - ее эпюра.
Положение проекций точки А на эпюре однозначно определяется ее тремя координатами АХ, АY, AZ (рис. 1.14).
На рис. 1.13 и рис. 1.14 также видно, что на эпюре горизонтальная и фронтальная проекции точки лежат на одном перпендикуляре к оси Х, а также фронтальная и профильная проекции - на одном перпендикуляре к оси Z:
А1А2 ┴ Х, А2А3 ┴ Z.
Из рис 1.12 видно, что точки, расположенные в различных октантах, имеют определенные знаки координат.
В таблице приведены знаки координат точек, расположенных в различных октантах
Таблица знаков координат
| Октанты | Знаки координат | ||
| Х | Y | Z | |
| + | + | + | |
| + | - | + | |
| + | - | - | |
| + | + | - | |
| - | + | + | |
| - | - | + | |
| - | - | - | |
| - | + | - |
2.1.Способы задания точки и прямой на комплексном чертеже
Точка, как математическое понятие, не имеет размеров. Очевидно, если объект проецирования является нульмерным образом, то говорить о его проецировании бессмысленно.
В геометрии под точкой целесообразно понимать физический объект, имеющий линейные измерения. Условно за точку будем принимать шарик с бесконечно малым радиусом. При такой трактовке понятия точки можно говорить о ее проекциях.
Прямая на комплексном чертеже может быть задана проекциями прямой; проекциями двух точек, принадлежащих прямой; проекциями отрезка прямой
2.2. Свойства прямой на комплексном чертеже
- 1. Прямая линия определяется двумя точками, поэтому на комплексном чертеже всякая прямая может быть задана проекциями двух ее точек. Прямую на комплексном чертеже можно задать и ее проекциями.
- 2. Всякая непрофильная прямая вполне определяется двумя своими проекциями, для определения же профильной прямой необходимо задать на проекциях прямой проекции ее двух точек
- 3. Чтобы задать на одной профильной прямой какую-нибудь точку, достаточно задать ее проекции на одноименных проекциях данной прямой.
- 4. Для деления данного отрезка в данном отношении достаточно разделить в этом отношении одну из проекций данного отрезка, а затем спроецировать делящую точку на другую проекцию отрезка.
2.3. Частные положения прямой в пространстве
На рис. 2.1 показаны прямые общего положения, т. е. прямые, произвольно расположенные относительно плоскостей проекций.
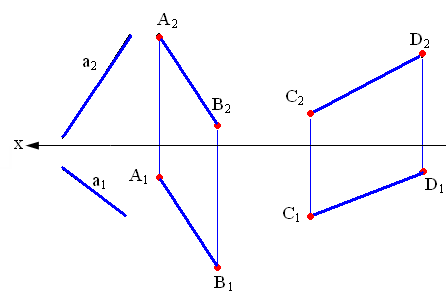
Рис. 2.1. Прямые общего положения
Особый интерес представляют прямые частного положения, т. е. прямые, расположенные определенным образом относительно плоскостей проекций: параллельные, перпендикулярные и принадлежащие плоскостям проекций.
Рассмотрим изображение на эпюре и отметим основные свойства этих прямых.
Прямые, параллельные плоскостям проекций
- 1. Горизонтальная прямая h (рис. 2.2) - горизонталь
Горизонтальная прямая - это прямая, параллельная горизонтальной плоскости проекций π1.
Так как все точки этой прямой равноудалены от плоскости проекций π1 (координаты Z всех точек прямой одинаковы), то фронтальная и профильная проекции прямой соответственно параллельны координатным осям Х и Y. На плоскость проекций π1проецируются без искажения отрезок прямой АВ (А1В1=АВ) и углы наклона прямой к плоскостям проекций π2 и π3 (углы β° и γ°).
- 2. Фронтальная прямая f (рис. 2.3) - фронталь
Фронтальная прямая - это прямая параллельная фронтальной плоскости проекций p2.
Так как все точки этой прямой равноудалены от плоскости проекций π2 (координаты Y всех точек прямой одинаковы), то горизонтальная и профильная проекции прямой соответственно параллельны координатным осям Х и Z. На плоскость проекций π2проецируются без искажений отрезок этой прямой CD (C2D2+CD) и углы наклона прямой к плоскостям проекций π1 и π3 (углы α° и γ°)
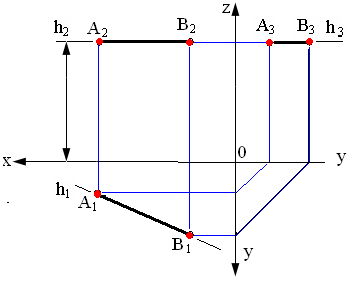
Рис. 2.2. Горизонтальная прямая на комплексном чертеже
- 3. Профильная прямая p (рис. 2.4)
Профильная прямая - это прямая, параллельная профильной плоскости проекций π3
Так как все точки этой прямой равноудалены от плоскости проекций π3 (координаты Х всех точек прямой одинаковы), то горизонтальная и фронтальная проекции прямой соответственно параллельны координатным осям Y и Z. На плоскость проекций p3проецируется без искажения отрезок этой прямой EF (E3F3=EF) и углы наклона прямой к плоскостям проекций π1 и π2 (углы α° и β°).
Прямые, принадлежащие плоскостям проекций
Прямые, принадлежащие плоскостям проекций, являются частным случаем горизонтальных, фронтальных и профильных прямых. Характерным признаком для эпюра, на котором изображена подобная прямая будет принадлежность одной из проекций прямой соответствующей оси.

Рис. 2.3. Изображение фронтальной прямой

Рис. 2.4. Изображение профильной прямой
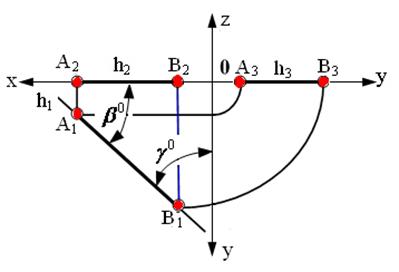
Рис. 2.5. Изображение прямой, принадлежащей горизонтальной плоскости проекций
На рис. 2.5, 2.6, 2.7 показаны прямые, принадлежащие соответственно горизонтальной плоскости проекций (частный случай горизонтальной прямой Z=0), фронтальной плоскости проекций (частный случай фронтальной прямой Y=0) и профильной плоскости проекций (частный случай профильной прямой Х=0).
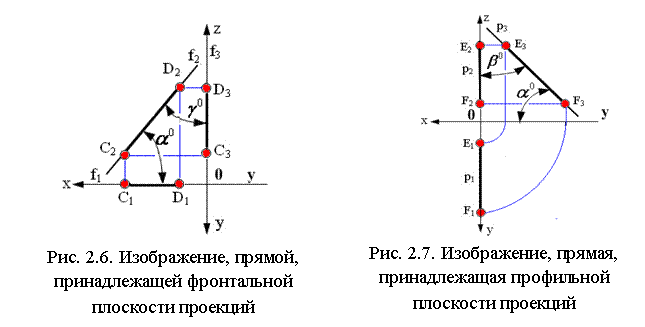
Прямые, перпендикулярные плоскостям проекций
Проецирующие прямые
На рис. 2.8, 2.9 и 2.10 показаны прямые на комплексном чертеже, перпендикулярные соответственно горизонтальной, фронтальной и профильной плоскостям проекций.
Прямая, перпендикулярная горизонтальной плоскости проекций - горизонтально-проецирующая прямая. Такая прямая проецируется на плоскость π1 в точку; ее фронтальная проекция перпендикулярна оси Х (рис. 2.8).
Прямая, перпендикулярная фронтальной плоскости проекций - фронтально-проецирующая прямая. Эта прямая проецируется на плоскость π2 в точку, а ее горизонтальная проекция перпендикулярна оси Х (рис. 2.9).
Прямая, перпендикулярная профильной плоскости проекций - профильно-проецирующая прямая. Эта прямая проецируется на плоскость π3 в точку, а ее фронтальная проекция перпендикулярна оси Z.
2.4. Следы прямой линии
Следом прямой линии называется точка пересечения прямой с плоскостью проекций.
В системе двух плоскостей проекций p1 и p2 прямая в общем случае имеет два следа:
- 1. Горизонтальный Н (Н1, Н2);
- 2. Фронтальный F (F1, F2).
Это точки пересечения прямой соответственно с горизонтальной и фронтальной плоскостями проекций (рис. 2.11, а).
Установим правило нахождения следов прямой.
Для нахождения горизонтального следа прямой необходимо:
1) продолжить фронтальную проекцию прямой а до пересечения с осью Х (получим точку НХ º Н2)
2) восстановить перпендикуляр в точке НХ к оси Х (провести линию связи перпендикулярную к оси Х);
3) продолжить горизонтальную проекцию прямой а до пересечения с перпендикуляром;
4) полученная точка пересечения и будет горизонтальным следом прямой а Н º Н1 (рис. 2.11, б).
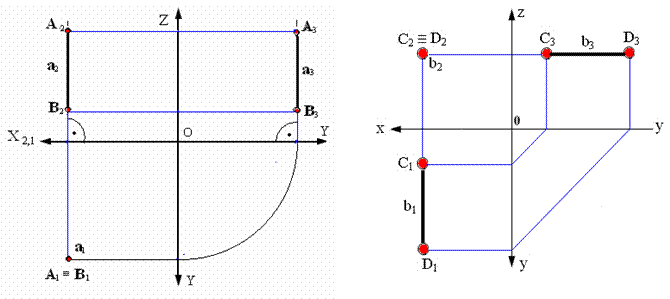
Рис. 2.8. Прямая, перпендикулярная Рис. 2.9. Прямая, перпендикулярная
горизонтальной плоскости проекций фронтальной плоскости проекций

Рис. 2.10. Прямая, перпендикулярная профильной плоскости проекций

а б
Рис. 2.11. Изображение следов прямой линии:
а - в пространстве; б - на эпюре
Для нахождения фронтального следа прямой необходимо:
1) продолжить горизонтальную проекцию прямой а до пересечения с осью Х (точка FXº F1);
2) восстановить перпендикуляр в точке FX к оси Х;
3) продолжить фронтальную проекцию прямой до пересечения с перпендикуляром;
4) полученная точка пересечения Fº F2 будет фронтальным следом прямой а (рис. 2.11, б).
В начертательной геометрии считается, что наблюдатель расположен в первом пространственном углу на бесконечном расстоянии от плоскостей проекций, поэтому видимыми геометрическими фигурами будут только те, которые расположены в первом октанте.
Проекции этих фигур в ортогональных и аксонометрических проекциях показываются сплошными линиями. Фигуры, расположенные в других пространственных углах, не видны наблюдателю, и их проекции показываются штриховыми линиями.
2.5. Плоскость. Способы задания плоскости на комплексном чертеже
На эпюре плоскость может быть задана графически одним из следующих способов, показанных на рис. 2.12.

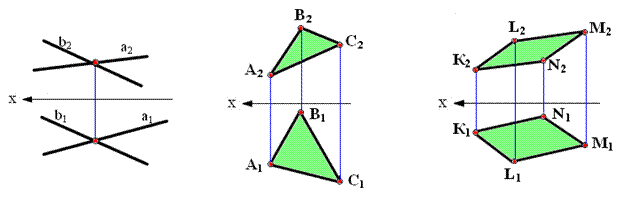

Рис. 2.12. Способы задания
плоскости:
а - тремя точками, не лежащими на одной прямой; б - прямой и точкой вне ее; в - двумя пересекающимися прямыми; г - двумя параллельными прямыми; д,е - плоской фигурой;
ж - следами плоскости
2.6. Общее и частные положения плоскости в пространстве
Плоскость общего положения
Плоскость, которая занимает произвольное положение по отношению к плоскости проекций (углы наклона этой плоскости к плоскостям проекций - произвольные, но отличные от 0° и 90°) называется плоскостью общего положения (рис. 2.12.а).
На комплексном чертеже следы плоскости общего положения составляют с осью проекций также произвольные углы.
Рассмотрим изображение на комплексном чертеже и свойства плоскостей частного положения: плоскости, перпендикулярные и параллельные плоскостям проекций.
Плоскости, перпендикулярные плоскостям проекций
(проецирующие плоскости)
- 1. Горизонтально-проецирующая плоскость α ┴ π1.
Плоскость α, перпендикулярная горизонтальной плоскости проекции π1, называется горизонтально проецирующей (рис. 2.13).
Основным свойством горизонтально-проецирующей плоскости является то, что любая фигура, расположенная в этой плоскости, проецируется на π1 в прямую линию (горизонтальный след плоскости h0α).
Угол b, который составляет горизонтальный след плоскости h0a c координатной осью Х, равен углу наклона плоскости a к плоскости проекций p2. Фронтальный след такой плоскости перпендикулярен оси Х (f0a ┴ X).
- 2. Фронтально-проецирующая плоскость β ┴ π2.
Плоскость b перпендикулярная фронтальной плоскости проекций π2 называется фронтально проецирующей (рис. 2.14).

а б в

г д е

ж
| Рис. 2.12. Способы задания плоскости: а - тремя точками, не лежащими на одной прямой; б - прямой и точкой вне ее; в - двумя пересекающимися прямыми; г - двумя параллельными прямыми; д,е - плоской фигурой; ж - следами плоскости |

Рис. 2.13. Горизонтально-проецирующая плоскость

Рис. 2.14. Фронтально-проецирующая плоскость
Основным свойством фронтально-проецирующей плоскости является то, что любая фигура, расположенная в этой плоскости, проецируется на π2 в прямую линию (фронтальный след плоскости f0β). Угол a, который составляет фронтальный след плоскости f0β с координатной осью Х, равен углу наклона плоскости b к плоскости проекций π1. Горизонтальный след такой плоскости перпендикулярен оси Х.
Плоскости, параллельные плоскостям проекций
(плоскости уровня)
1. Горизонтальная плоскость γ || π1.
Плоскость γ, параллельная плоскости π1, называется горизонтальной (рис. 2.15).
Любая фигура, расположенная в такой плоскости, проецируется на горизонтальную плоскость проекций в натуральную величину (Δ А1В1С1 = ΔАВС, рис. 17). Фронтальный след этой плоскости параллелен оси Х (f0g | | Х).
2. Фронтальная плоскость δ | | π2.
Плоскость δ, параллельная плоскости π2, называется фронтальной.
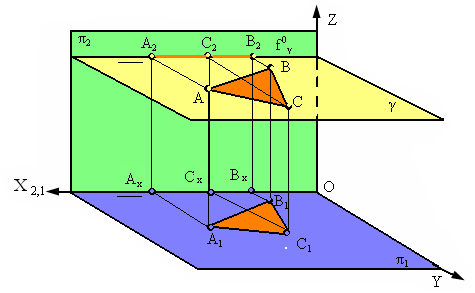
Рис. 2.15. Плоскость, параллельная горизонтальной плоскости проекций
Любая фигура, расположенная в такой плоскости, проецируется на фронтальную плоскость проекций без искажения, т. е. в натуральную величину.
Горизонтальный след фронтальной плоскости параллелен оси Х.
Примечание. Плоскость, параллельная одной из плоскостей проекций, является частным случаем проецирующих плоскостей.
2.7. Следы плоскости
Следом плоскости a называется линия пересечения этой плоскости с плоскостью проекций.
В системе двух плоскостей проекций π1 и π2 плоскость в общем случае имеет два следа: горизонтальный ha0 и фронтальный fa0, которые являются пересечением плоскости a соответственно с горизонтальной и фронтальной плоскостями проекций (рис. 2.16).
Точки пересечения плоскости a с координатными осями X, Y, Z называются точками схода следов и обозначаются соответственно Sx, Sy, Sz
(рис. 2.16.а).
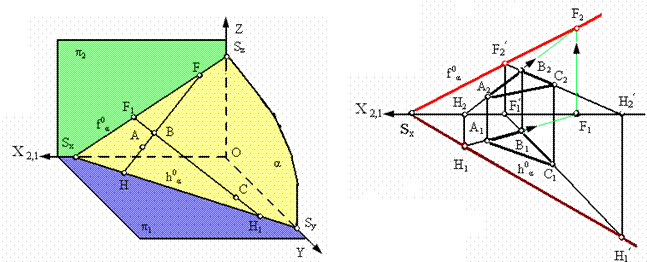
а б
Рис. 2.16. Пример изображения следов плоскости:
а - в пространстве; б - на комплексном чертеже
3.1. Определение позиционных задач
Позиционными задачами называются такие задачи, в которых определяется взаимное расположение различных объектов и элементов геометрических фигур относительно друг друга.
3.2. Метод конкурирующих точек
Метод конкурирующих точек используется в начертательной геометрии для определения взаимной видимости двух геометрических фигур.
Конкурирующими точками называются такие точки пространства, которые имеют одинаковые координаты в плоскости проекций.
На рис. 3.1 показаны конкурирующие точки А и В (совпадают горизонтальные проекции А1 ≡ В1) и C и D (совпадают фронтальные проекции С2 ≡ D2).
Метод конкурирующих точек заключается в определении взаимной видимости точек (фигур) по координатам их несовпадающих проекций. Точка В находится выше точки А относительно плоскости π1 (ZB>ZA), поэтому на плоскости π1видна точка В, которая закрывает точку А (считается, что наблюдатель смотрит на плоскости проекций из бесконечности и направление луча зрения параллельно проецирующему лучу S).
На плоскости π2 видна точка D, так как она находится ближе к наблюдателю (дальше от плоскости π2, YD>YC) и закрывает невидимую точку С.
Методом конкурирующих точек пользуются при определении видимости элементов пересекающихся геометрических фигур.
3.3. Прямая и точка
Из инвариантного свойства 3 параллельного проецирования следует, что проекции точки К (К1, К2 и К3) принадлежащие прямой а, должны принадлежать соответствующим проекциям этой прямой, т. е. если хотя бы одна проекция точки не принадлежит соответствующей проекции прямой, то эта точка не принадлежит прямой.
Из инвариантного свойства 4 следует, что проекции точки К (К1, К2 и К3), принадлежащие прямой АВ, делят соответствующие проекции отрезка в том же отношении, в каком точка К делит отрезок АВ (рис. 3.2).

Рис. 3.1. Конкурирующие точки
Точки А и В, принадлежащие прямой а, и точки C, D и E, которые лежат вне этой прямой показаны на рис. 3.3.
3.4. Взаимные положения прямых
Две прямые в пространстве могут пересекаться, скрещиваться и могут быть параллельны.
1. Пересекающиеся прямые
Пересекающимися прямыми называются такие прямые, которые имеют одну общую точку.
Из инвариантного свойства 5 следует, что проекция точки пересечения проекций прямых а и b есть точка пересечения этих прямых (рис. 3.4).
2. Параллельные прямые
На рис. 3.5 изображены параллельные прямые - прямые, пересекающиеся в несобственной точке (прямые, лежащие в одной плоскости и пересекающиеся в бесконечно удаленной точке).
Из инвариантного свойства 6 следует, что проекции параллельных прямых а и b параллельны.
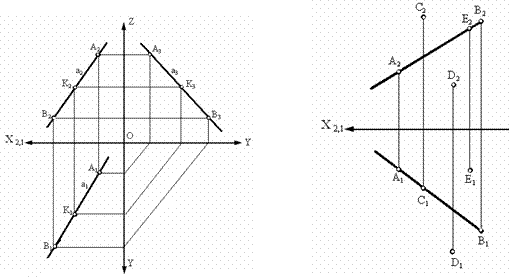
Рис. 3.2. Изображение принадлежности Рис. 3.3. Пример принадлежности
точек А, В, К прямой а точек прямой
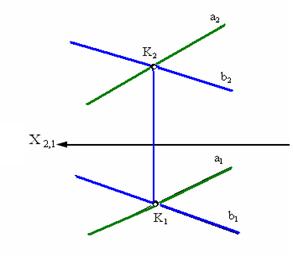
Рис. 3.4. Пересекающиеся прямые
3. Скрещивающиеся прямые
Скрещивающиеся прямые - это прямые, не лежащие в одной плоскости, это прямые не имеющие ни одной общей точки.
На комплексном чертеже (рис. 3.6) точки пересечения проекций этих прямых не лежат на одном перпендикуляре к оси Х (в отличие от пересекающихся прямых, см. рис. 3.4).

| Рис. 3.5. Параллельные прямые Рис. 3.6. Скрещивающиеся прямые |
3.5. Прямая и точка на плоскости
Прямая АВ принадлежит плоскости α, если две ее точки А и В принадлежат этой плоскости α. (∆КLM) Справедливо и обратное утверждение: если точки А и В принадлежат плоскости α ((∆КLM), то пряма АВ, проходящая через эти точки, принадлежит плоскости α.
Прямые АВ и CD, принадлежащие разным плоскостям показаны на рис. 3.7. Прямая АВ принадлежит плоской фигуре LKM, потому что на проекциях прямой и плоской фигуры имеются две общих точки (рис. 3.7, а). Прямая CD принадлежит плоскости, заданной параллельными прямыми с и d, т. к. она проходит через точки С и D, расположенные на этих прямых (рис. 3.7, б).
Прямая принадлежит плоскости, если ее следы принадлежат одновременно следам плоскости.
Справедливо и обратное утверждение: если следы прямой принадлежат следам плоскости, то эта прямая принадлежит плоскости.
Кроме того, существует еще одно свойство, определяющее взаимное положение точки и плоскости: точка принадлежит плоскости, если она расположена на прямой, принадлежащей этой плоскости (рис. 3.7).
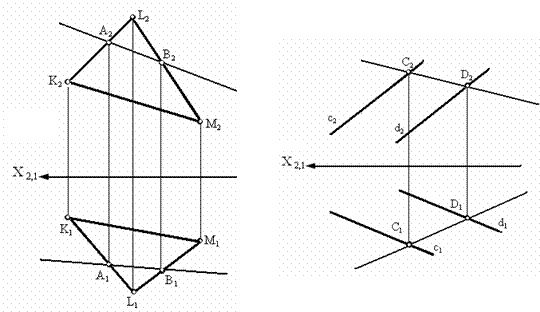
а б
Рис. 3.7. Изображение прямых, принадлежащих плоскостям
3.6. Взаимное положение прямой и плоскости
Рассмотрим два случая взаимного положения прямой и плоскости: прямая параллельная и перпендикулярная плоскости.
•1. Прямая параллельная плоскости.
Прямая параллельна плоскости, если она параллельна прямой b, принадлежащей этой плоскости.
Прямые, параллельные плоскостям, заданные различными способами показаны на рис. 3.8.
•2. Прямая перпендикулярная плоскости.
Прямая перпендикулярна плоскости, если она перпендикулярна
двум пересекающимся прямым этой плоскости.
Подробно перпендикулярность прямых рассмотрена в главе 4.
3.7. Пересечение прямой и плоскости
Для рассмотрения пересечения прямой и плоскости целесообразно начать с рассмотрения случая пересечения двух плоскостей (рис. 3.9), когда одна из пересекающихся плоскостей параллельна горизонтальной плоскости проекций (α | | π1, f0α | | Х). В этом случае линия пересечения а, принадлежащая плоскости α, будет также параллельна плоскости π1, (рис. 3.9. а), т. е. будет совпадать с горизонталью пересекающихся плоскостей (а ≡ h).
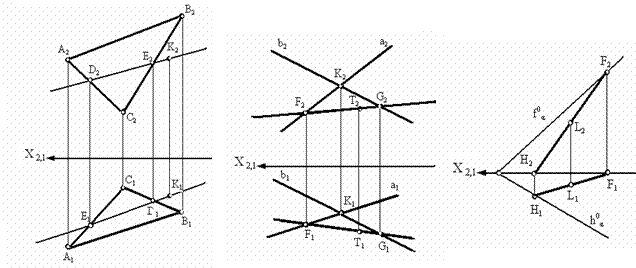
а б в
Рис. 3.8. Прямые, параллельные плоскостям, заданным:
а - плоскостью треугольника АВС;
б - двумя пересекающимися прямыми а ∩ b;
в - горизонтальным h0α и фронтальным f0α следами
Если одна из плоскостей параллельна фронтальной плоскости проекций (рис. 3.9. б), то линия пересечения а, принадлежащая этой плоскости, будет параллельна плоскости π2и будет совпадать с фронталью пересекающихся плоскостей (а ≡ f).
Пример построения точки пересечения (К) прямой а (АВ) с плоскостью α (DEF) показан на рис. 3.10. Для этого прямая а заключена в произвольную плоскость β и определена линия пересечения плоскостей α и β.
В рассматриваемом примере прямые АВ и MN принадлежат одной плоскости β и пересекаются в точке К, а так как прямая MN принадлежит заданной плоскости α (DEF), то точка К является и точкой пересечения прямой а (АВ) с плоскостью α. (рис. 3. 11).
Для решения подобной задачи на комплексном чертеже необходимо уметь находить точку пересечения прямой общего положения с плоскостью общего положения.
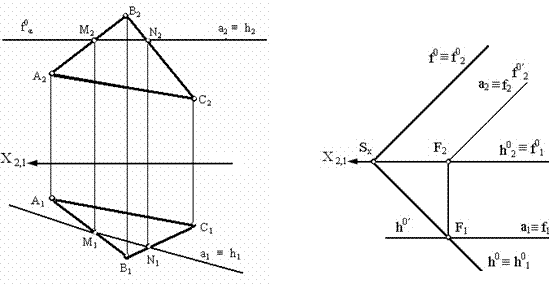
а б
Рис. 3.9. Частный случай пересечения плоскости общего положения с плоскостями: а - горизонтального уровня; б - фронтального уровня
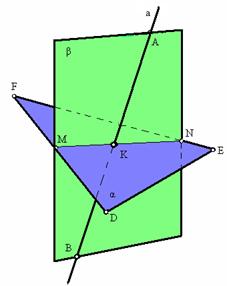
| Рис. 3. 10. Построение точки пересечения прямой с плоскостью |
Рассмотрим пример нахождения точки пересечения прямой АВ c плоскостью треугольника DEF представленный на комплексном чертеже (рис. 3.11).
Для нахождения указанной точки пересечения через фронтальную проекцию прямой А2В2 проведена фронтально проецирующая плоскость β которая пересекла треугольник по прямой MN. На фронтальной плоскости проекций (π2) эта прямая представлена проекциями двух точек M2, N2. Из условия принадлежности прямой плоскости на горизонтальной плоскости проекций (π1) находятся горизонтальные проекции полученных точек M1 N1. В пересечении горизонтальных проекций прямых А1В1 и M1N1 образуется горизонтальная проекция точки их пересечения (К1). По линии связи и условиям принадлежности на фронтальной плоскости проекций находится фронтальная проекция точки пересечения (К2).
Видимость отрезка АВ относительно треугольника DEF определена методом конкурирующих точек.
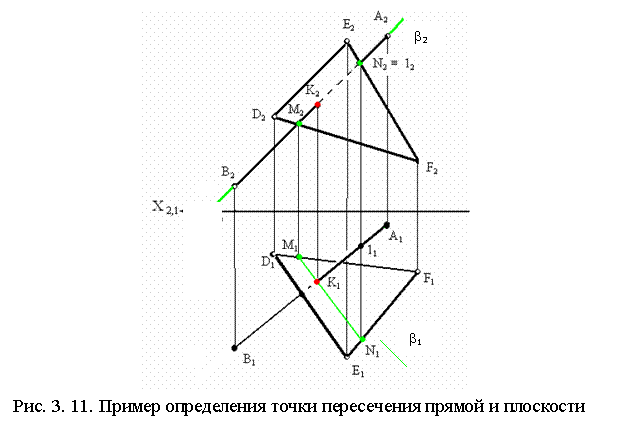
На плоскости π2 рассмотрены две точки N ∈ EF и 1∈ AB. По горизонтальным проекциям этих точек можно установить, что точка N расположена ближе к наблюдателю (YN>Y1), чем точка 1 (направление луча зрения параллельно S). Следовательно, прямая АВ, т. е. часть прямой АВ (К1) закрыта плоскостью DEF на плоскости π2 (ее проекция К212 показана штриховой линии). Аналогично установлена видимость на плоскости π1. Определение видимости прямой в горизонтальной плоскости проекций можно при выполнении аналогичных операций.
4.1.Условие перпендикулярности двух прямых на комплексном чертеже
Особый интерес с точки зрения решения задач начертательной геометрии представляют перпендикулярные прямые.
Из классической Евклидовой геометрии известно следующее свойство перпендикулярности двух прямых:
Две прямые перпендикулярны, если угол между ними составляет 90°.
Кроме того, в начертательной геометрии существует еще одно утверждение на эту тему:
Две прямые перпендикулярны, если одна из них линия уровня.
Для подтверждения этого заключения рассмотрим примеры, приведенные на рис. 4.1.
Предположим что необходимо через точку А провести прямую ℓ, пересекающую горизонталь h прямым углом ℓ ┴ h (рис. 4.1.а).
Так как одна из сторон h прямого угла параллельна плоскости π1, то на эту плоскость прямой угол спроецируется без искажения. Поэтому через горизонтальную проекцию А1 проведем горизонтальную проекцию искомой прямой ℓ1┴ h1. Отметим горизонтальную проекцию точки пересечения прямой и горизонтали M1= ℓ1 ∩ h1. Найдем по принадлежности фронтальную проекцию точки пересечения M2. Точки А2 и M2 определяют фронтальную проекцию искомой прямой ℓ. Две проекции прямой определяют ее положение в пространстве.
Если вместо горизонтали будет задана фронталь f, то геометрические построения по проведению прямой ℓ ┴ f аналогичны рассмотренным с той лишь разницей, что построения неискаженной проекции прямого угла следует начинать с фронтальной проекции (рис. 4.1.б).
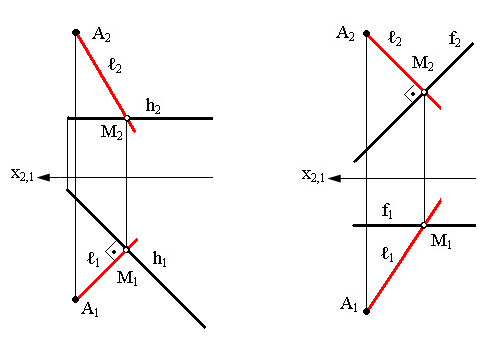
а б
Рис. 4.1. Примеры построения перпендикулярных прямых:
а) прямая l, перпендикулярна к горизонтали (h); ℓ ┴ h;
б) прямая l, перпендикулярна к фронтали (f); ℓ ┴ f
4.2. Условие перпендикулярности прямой и плоскости
Прямая а перпендикулярна плоскости α, если она перпендикулярна двум пересекающимся прямым b и с этой плоскости.
Если прямые b и с, принадлежащие плоскости α, расположены произвольно относительно плоскостей проекций, то прямые углы между прямой а и прямыми b и с спроецируются на плоскость проекций с искажениями.
Для того чтобы эти прямые углы спроецировались в натуральную величину, прямые b и с должны быть параллельны плоскостям проекций, т. е. являться соответственно горизонталью и фронталью плоскости α..
Прямая а перпендикулярна плоскости α, если она перпендикулярна пересекающимся горизонтали (h) и фронтали (f) этой плоскости.
При этом прямые углы между прямой а и прямыми h и f на соответствующие плоскости проекций спроецируются без искажений.
Кроме вышесказанного существует теорема:
Для того чтобы прямая в пространстве была перпендикулярна плоскости, необходимо и достаточно, чтобы на эпюре горизонтальная проекция прямой была перпендикулярна к горизонтальной проекции горизонтали плоскости, а фронтальная проекция - к фронтальной проекции фронтали этой плоскости.
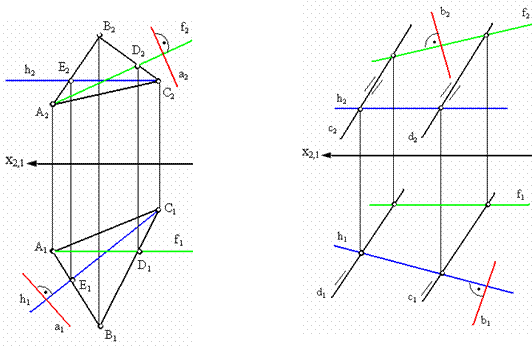
а б
Рис. 4.2. Изображение прямых, перпендикулярных к плоскостям заданным:
а - плоскостью фигуры АВС; б - прямыми c, d
Следовательно, прямая а перпендикулярна плоскости α, если ее проекции перпендикулярны соответствующим проекциям горизонтали h и фронтали f этой плоскости.
На рис. 4.2 изображены прямые а, b, c перпендикулярные плоскостям, заданным различными способами.
Если плоскость задана следами, то горизонталью и фронталью плоскости являются ее пересекающиеся следы.
Следовательно, прямая а перпендикулярна плоскости α, если ее проекции перпендикулярны соответствующим пересекающимся следам плоскости
(рис. 4.3).

Рис.4.3. Изображение прямой а перпендикулярной к плоскости,
заданной следами
4. 3. Условие перпендикулярности двух плоскостей
Плоскости α и β перпендикулярны, если одна плоскость проходит через перпендикуляр другой плоскости.
На рис. 4.3 показана прямая а перпендикулярная плоскости α, (следовательно, любая плоскость, проходящая через прямую а, будет перпендикулярна плоскости α). На рис. 4.4 изображены две проецирующие плоскости β и γ и произвольная плоскость δ, следы которой проходят через следы прямой а.
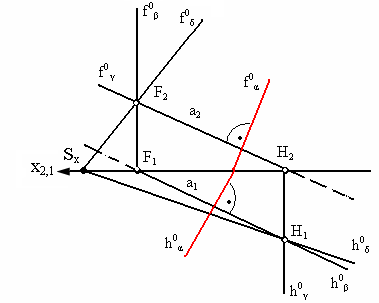
Рис. 4.4. Условие перпендикулярности плоскостей
На рис. 4.5 изображена прямая b, перпендикулярная плоскости Δ АВС, следовательно, любая плоскость, проходящая через прямую b, будет перпендикулярна плоскости Δ АВС.

Рис. 4.5. Условие перпендикулярности плоскостей
4.4. Определение длины отрезка и углов его наклона к плоскостям проекций
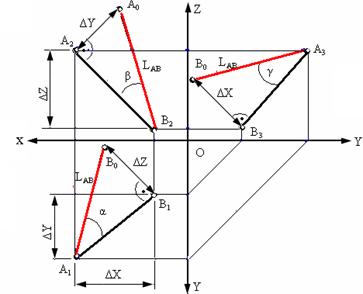
Рис. 4.6. Определение длины отрезка и углов наклона
к плоскостям проекций
На рис. 4.6 показан пример определения длины отрезка АВ и углов наклона его к плоскостям проекций.
Длина отрезка АВ равна гипотенузе этого треугольника, катетами которого являются горизонтальная проекция отрезка А1В1 и разность координат z точек А и В (Δz = zA- zB).
Как известно, угол наклона прямой к плоскости равен углу между этой прямой АВ и ее проекцией на плоскость (А1В1).
Следовательно, угол Δ АВВ', лежащий против катета Δz, равен углу наклона отрезка АВ и горизонтальной плоскости проекций π1 (угол α°).
Аналогично рассуждая (рис. 4.6), можно показать, что длина отрезка АВ равна гипотенузе треугольника, катетами которого являются фронтальная проекция отрезка А2В2 и разность координат Y точек А и В (ΔY =YA- YB).
Угол этого треугольника, лежащий против катета ΔY, равен углу наклона отрезка АВ к фронтальной плоскости проекций π2 (угол β°).
По аналогии длина отрезка АВ может быть определена и как гипотенуза треугольника, катеты которого профильная проекция отрезка А3В3 и разность координат Х (Δ Х = ХА - ХВ) точек А и В. Угол γ° этого треугольника, лежащий против катета Δ Х, определяет угол наклона отрезка АВ к профильной плоскости проекций π3. (рис. 4.6).
4.5. Линии наибольшего наклона (ската)
Линией наибольшего наклона (ската) плоскости γ называется прямая g, принадлежащая этой плоскости и перпендикулярная ее линиям уровня: горизонтали h и фронтали f (рис. 4.7).
На комплексном чертеже горизонтальная проекция линии наибольшего наклона перпендикулярна горизонтальной проекции горизонтали этой плоскости, а фронтальная - фронтальной проекции фронтали.
Главным свойством этой линии наибольшего ската является то, что она образует с горизонтальной плоскостью проекций π1 угол α°, равный углу наклона плоскости γ к плоскости π1.

Рис. 4.7. Пример построения линии наибольшего наклона
Это свойство линии наибольшего наклона (ската) используется для определения углов наклона плоскостей к плоскостям проекций.
5.1. Необходимость преобразований комплексного чертежа
Трудоемкость и, как следствие, точность графического решения задач часто зависят не только от сложности задач, но и от того, какое положение занимают геометрические фигуры, входящие в условие задачи, по отношению к плоскостям проекций.
Проецируемая фигура может занимать по отношению к плоскостям проекций произвольное, или частное положение.
В первом случае, как правило, получаются проекции, неудобные для решения задач. Решение задачи значительно упрощается, когда мы имеем дело с частным расположением геометрических фигур относительно плоскостей проекций. Наиболее выгодным частным положением проецируемой фигуры при ортогональном проецировании следует считать:
1) положение, перпендикулярное к плоскости проекций - при решении позиционных задач;
2) положение, параллельное плоскости проекций - для решения метрических задач.
Таким образом, при решении той или иной задачи бывает целесообразно привести фигуру к частному положению.
Переход от общего положения геометрической фигуры к частному можно осуществлять изменением взаимного положения проецируемой фигуры и плоскости проекции. При ортогональном проецировании это может быть достигнуто двумя путями:
1) перемещением в пространстве проецируемой фигуры, по отношению к плоскости проекций.
2) выбором новой плоскости проекций, по отношению к проецируемой фигуре.
Первый путь лежит в основе плоскопараллельного перемещения; второй - составляет теоретическую базу способа замены плоскостей проекций.
5.2. Задачи на преобразование комплексного чертежа
Все метрические и позиционные задачи можно свести к одной из следующих четырех задач.
Задача №1. Преобразовать комплексный чертеж так, чтобы прямая общего положения АВ оказалась параллельной одной из плоскостей проекций т.е. стала прямой уровня (горизонталь или фронталь) новой системы.
Для решения задачи необходимо заменить плоскость проекций П1, или П2 новой плоскостью проекций П4, параллельной прямой АВ и перпендикулярной к незаменяемой плоскости проекций. Для того чтобы прямая АВ в новой системе плоскостей проекций стала, например, фронталью, нужно заменить фронтальную плоскость проекций П2 новой плоскостью П4 ┴ П1 и параллельной прямой АВ (рис. 5.1, а).
Рассмотрим подробно этапы построения на комплексном чертеже
(рис. 5.1, б), необходимые для решения первой основной задачи на преобразование комплексного чертежа:
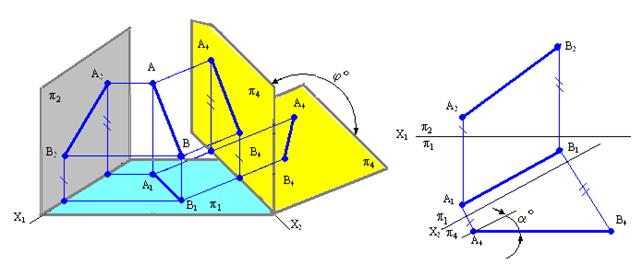
а б
Рис. 5.1. Изображение преобразования прямой общего положения
в прямую положения уровня:
а - в пространстве; б - на комплексном чертеже
1) провести новую ось проекций х14 параллельно А1В1 на произвольном расстоянии от нее; такое положение оси х14 обусловливается тем, что П4 параллельна АВ. В частном случае, если плоскость П4 проведена непосредственно через прямую АВ, ось х14 = А1В1;
2) выбрать на прямой две точки А(А1А2) и В(В1В2);
3) построить проекции точек А и В на плоскости П4.
Прямая А4В4 является проекцией прямой АВ на плоскость П4. Прямая AB в новой системе плоскостей проекций П1/П4 является фронталью.
Отрезок [АВ] прямой проецируется на плоскость П4 в истинную величину, т.е. | А4В4 | = | АB |, a- величина угла наклона прямой АВ к плоскости П1.
3адача 2. Преобразовать комплексный чертеж так, чтобы линия общего положения АВ стала проецирующей.
Для решения задачи необходимо заменить плоскость П2 исходной системы П2/П1плоскостью П4 // А1В1, при этом плоскость П4 будет перпендикулярной П1 так как АВ // П4 и образует с ней новую систему плоскостей проекций П1/П4.
Последовательность построений на комплексном чертеже показана на рис. 5.2:
1) провести новую ось проекций х14 // А1В1;
2) построить проекции точек А и В на плоскости П4, взяв координаты точек из плоскости П2;
3) заменить плоскость П1 на новую П5, которая будет П4 и А4В4. Для этого нужно провести новую ось проекций х4,5.
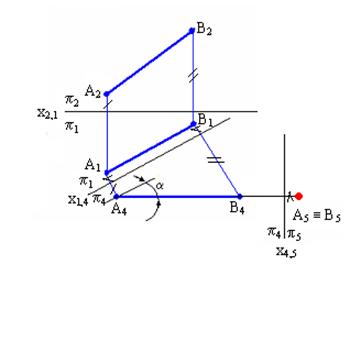
| Рис. 5.2. Преобразование прямой АВ общего положения в горизонтально-проецирующую. |
Так как расстояния точек А и В до плоскости П4 одинаковы, то проекции их на плоскости П5 совпадут, А5 ≡ В5, прямая АВ (А5В5) в новой системе плоскостей проекций заняла проецирующее положение и стала горизонтально проецирующей. Прямую общего положения преобразовать в проецирующую заменой только одной плоскости проекций нельзя, так как плоскость П5 перпендикулярная прямой, не будет перпендикулярна ни одной из «старых» плоскостей проекций, и, следовательно, не сможет образовать ни с одной из них прямоугольной системы плоскостей проекций.
Для того чтобы прямую общего положения преобразовать в проецирующую, необходимо выполнить две последовательные замены плоскостей проекций. Прямую общего положения следует преобразовать в линию уровня, а затем линию уровня преобразовать в проецирующую (рис. 5.2).
Задача №3. Преобразовать комплексный чертеж так, чтобы плоскость общего положения стала проецирующей (рис. 5.3).
Для решения задачи необходимо заменить плоскость П1 или П2 исходной системы П2/П1 новой плоскостью П4, перпендикулярной плоскости (АВС). Две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную к другой плоскости. Следовательно, если какую-либо прямую, принадлежащую плоскости ∑ преобразовать в проецирующую, то плоскость в новой системе плоскостей проекций станет проецирующей.
Проще всего для этой цели воспользоваться линией уровня.
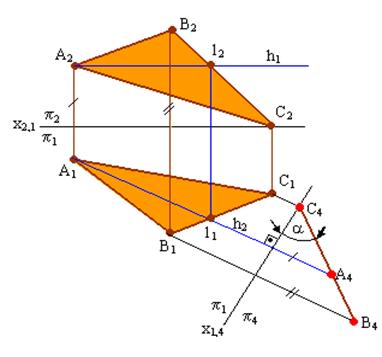
Рис. 5.3. Преобразование плоскости общего положения в проецирующую
На чертеже плоскость ∑ (АВС) преобразована во фронтально проецирующую (см. рис. 5.3) путем преобразования горизонтали h (h1,h2), принадлежащей плоскости ∑, во фронтально- проецирующую прямую. В новой системе плоскостей проекций П1/П4плоскость ∑ является фронтально проецирующей (∑┴ 4), и поэтому ее проекция на П4вырождается в прямую линию ∑4 (С4, А4, В4).
α - величина угла наклона плоскости ∑ к плоскости П1.
Задача №4. Преобразовать комплексный чертеж так, чтобы плоскость общего положения стала плоскостью уровня (параллельной одной из плоскостей проекций) новой системы.
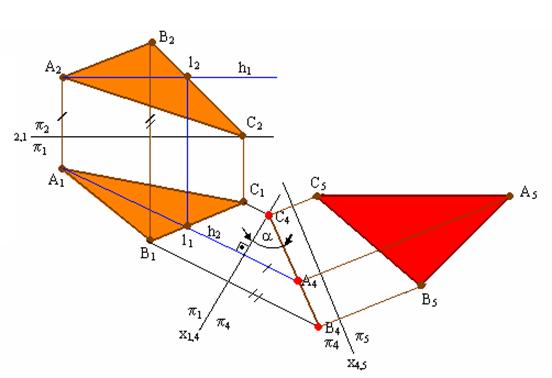
Рис. 5.4. Решение 4-й задачи на преобразование
плоскости общего положения в плоскость уровня
Плоскость общего положения преобразовать в плоскость уровня заменой только одной плоскости проекций нельзя, так как плоскость П4, параллельная ей, не будет перпендикулярна ни одной из старых плоскостей проекций и, следовательно, не образует ни с одной из них прямоугольной системы плоскостей проекций.
Для того чтобы плоскость общего положения преобразовать в плоскость уровня, необходимо выполнить две последовательные замены плоскостей проекций.
Вначале плоскость необходимо преобразовать в проецирующую, т. е. решить задачу 3 на преобразование комплексного чертежа, а затем проецирующую плоскость преобразовать в плоскость уровня. На рис. 5.4 показано преобразование плоскости ∆АВС в горизонтальную плоскость уровня.
6.1. Общие положения
Метрическими называются задачи, связанные с измерением расстояний и углов. В них определяются действительные величины и форма геометрических фигур, расстояния между ними и другие характеристики по их метрически искаженным проекциям. Решение метрических задач основано на том, что геометрическая фигура, принадлежащая плоскости, параллельной плоскости проекций, проецируется на нее в конгруэнтную ей фигуру (см. аксиомы параллельного проецирования). Поэтому при решении метрических задач широко используются способы преобразования комплексного чертежа.
Рассмотрим три группы метрических задач. К первой относятся задачи, в которых требуется найти расстояние между двумя геометрическими фигурами; ко второй - задачи на определение действительных величин плоских фигур и углов; к третьей группе принадлежат задачи, связанные с построением в плоскости общего положения геометрических фигур по заданным размерам.
6.2. Задачи на определение расстояний между геометрическими фигурами
Искомое расстояние во всех задачах этой группы измеряется длиной отрезка, заключенного между заданными геометрическими фигурами и перпендикулярного к одной из них или одновременно к обеим. Этот отрезок проецируется в конгруэнтный ему отрезок на плоскость проекций, которая будет перпендикулярна одной или обеим геометрическим фигурам, между которыми определяется расстояние. Алгоритм решения задач этой группы будет следующим:
1. Одним из способов преобразования комплексного чертежа привести обе заданные геометрические фигуры (или одну из них) в положение, перпендикулярное какой-либо плоскости проекций.
2. Построить проекцию искомого отрезка на эту плоскость. Выбирая способ преобразования комплексного чертежа при составлении алгоритма, следует учитывать требования к компактности чертежа, четкость и возможную простоту графических операций.
Задача 1. Определение расстояния от точки М до прямой АВ общего положения (рис. 6.1).
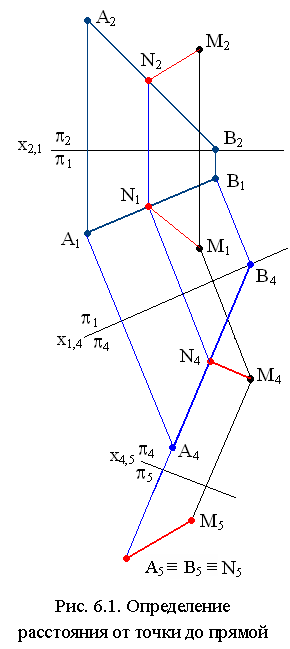
Искомое расстояние измеряется длиной отрезка /МN/ перпендикуляра, опущенного из точки М на прямую АВ. Отрезок [МN] спроецируется в конгруэнтный ему отрезок на плоскость проекций, перпендикулярную прямой АВ. Составляем алгоритм решения:
1. Преобразовать прямую АВ в проецирующую прямую способом замены плоскостей проекций.
2. Построить проекцию отрезка [МN] на плоскость П5 ┴АВ, длина которого М5N5определяет искомое расстояние.
Построение. Для преобразования прямой АВ общего положения в проецирующую выполнены две последовательные замены плоскостей проекций: вначале прямая АВ преобразована в линию уровня, затем линия уровня преобразована в проецирующую прямую. Построены проекций М4 и М5 точки М в системе П4/П5.
Отрезок [М5N5] является искомым: [М5N5] ≅ [МN] и /М5N5/ = /МN/.На рис. 6.1 показано построение проекций [М4N4], [М1N1] и [М2М2] отрезка [МN] обратным преобразованием.
Задача 2. Определить расстояние между параллельными прямыми а и b.
Для решения задачи необходимо выполнить две замены плоскостей проекций. Вначале прямые a и b необходимо сделать прямыми уровня. Для этого П4необходимо расположить параллельно a1 и b1. Затем названные прямые необходимо расположить перпендикулярно П5. Расстояние между а5 и b5 будет натуральной величиной между параллельными прямыми a и b (рис. 6.2).

Рис. 6.2. Определение расстояния между параллельными прямыми
Задача 3. Определение расстояния от точки до плоскости.
Решение задачи приведено на рис. 6.3.
Для определения расстояния от точки М до плоскости треугольника ∆АВС необходимо плоскость треугольника общего положения ∆АВС преобразовать в плоскость проецирующую. Для этого нужно произвести замену плоскости проекций П2 на П4 перпендикулярно h1.
Плоскость ∆АВС преобразуется в линию С4А4В4. На эту же плоскость П4спроецируется точка М (М4). Перпендикуляр из М4 на линию С4А4В4 будет натуральной величиной расстояния от точки М до плоскости ∆АВС. Проекции перпендикуляра переносятся в плоскости проекций П1 и П2 по соответствующим линиям связи, расстояния от точки М до плоскости ∆АВС. Проекции перпендикуляра переносятся в плоскости проекций П1 и П2 по соответствующим линиям связи.
Примечания: 1) Проекция перпендикуляра М1N1 в П1 располагается параллельно П4, потому что в плоскости П4 имеется ее натуральная величина.
2) Задачи 1- 3 можно также решать по следующей схеме: вначале определить метрически искаженные проекции искомого отрезка, а затем способом прямоугольного треугольника определить его действительную в






