Правила приближенных вычислений

При решении задач по электротехнике и электронике числовые значения, с которыми приходится иметь дело, большей частью являются приближенными. Задачи с приближенными данными следует решать, учитывая правила приближенных вычислений.

Правила приближенных вычислений состоят в следующем.

1.Учитывать количество значащих цифр, необходимых для соблюдения определенной точности вычислений. Значащими называют все цифры, кроме нуля, а также нуль в двух случаях: а) когда он стоит между значащими цифрами; б) когда он стоит в конце числа и известно, что единицы соответствующего разряда в данном числе нет. Например:

1603 - 4 значащих цифры;

1,03 - 3 значащих цифры;

1,00 - 3 значащих цифры;

0,00103 - 3 значащих цифры.

2. Так как с помощью вычислений получить результат более точный, чем исходные данные невозможно, то достаточно производить вычисления с числами, содержащими не более знаков, чем в исходных данных.

3. При сложении или вычитании приближенных чисел, имеющих различную точность, более точное должно быть округлено до точности менее точного. Например:

9.6 + 0.176 = 9.6 + 0,2 = 9.8

100,8 - 0,427 = 100,8 -0.4 = 100.4

4. При умножении и делении следует в полученном результате сохранять столько значащих цифр, сколько их имеет приближенное данное с наименьшим количеством значащих цифр. Например:

0.637 × 0.023 = 0.0132 но не 0.0132496;

6.32: 3 = 2 но не 2.107.

5. При возведении в квадрат или куб нужно сохранять столько значащих цифр, сколько их имеет возводимое в степень число. Например:

1.25² = 1.56, но не 1.5625;

1.01³ = 1.03, но не 1.030301.

6. При извлечении квадратного и кубического корней в результате нужно сохранять столько значащих цифр, сколько их имеет подкоренное число. Например:

10^1/2 = 3.1, но не 3.162;

10^1/3 = 2.1, но не 2.154.

7. При вычислении сложных выражений соблюдаются правила в зависимости от вида производимых действий.

8. Когда число мало отличается от единицы, можно пользоваться ниже приведенными приближенными формулами.

Если a, b, c малы по сравнению с единицей (меньше 0.1), то:

(1±a) ×(1±b) ×(1±c) = 1 ± a ± b ± c;

(1±a)^1/2 = 1± a/2; (1±a)ⁿ = 1± n × a;

1/ (1±a)ⁿ = 1 + n × a;

е^а = 1+a; ln(1±a) =±a - a²/2;

Если угол меньше 5⁰ и выражен в радианах, то в первом приближении можно принять sin a» tg a» a; cos a» 1.

Соблюдая эти правила, студент сэкономит время на вычислениях при решении задач по электротехнике и электронике.

Основные законы и формулы электротехники

Сила тока I = dq/dt

Закон Ома для замкнутой цепи I = e/ (R + r)

Закон Джоуля -Ленца для пост. тока Q = I²R t

То же для тока, зависящего от времени Q = ò I²(t)Rdt

Сопротивление однородного проводника R = r ℓ /S

Первый закон Кирхгофа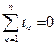

Второй закон Кирхгофа

Ток через индуктивность i=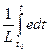

Ток через емкость i=C

Реактивное сопротивление индуктивности X_L=ωL

Реактивное сопротивление емкости X_C=

Полное реактивное сопротивление

последовательно соединенных элементов

Мощность в цепи переменного тока:

активная P = I·U cos φ

реактивная Q = I·U sin φ

полная S = I·U

Мощность в трехфазных цепях при симметричной нагрузке

активная P= 3 I_ф·U_ф cos φ = I_л·U_л cos φ

реактивная Q= 3 I_ф·U_ф sin φ = I_л·U_л sin φ

полная S= 3 I_ф·U_ф= I_л·U_л

Среднее значение в цепи переменного тока А_ср= 2А_мах/π ≈ 0,637 А_мах

Действующее значение в цепи переменного тока А = А_мах/ ≈ 0,707 А_мах,

где А – эдс, сила тока, напряжение, магнитный поток и т.д.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

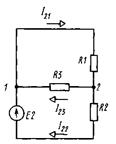
Пример 1. Два источника питания с эдс Е₁ = 60 В и Е₂ = 75 В включены в дифференциальную схему, как показано на рис. 1. Найти ток общей ветви, если сопротивление резисторов R₁ = 2 Ом; R₂ = 3 Ом; R₃ = 5 Ом.

Решение.На примере данной задачи рассмотрим основные методы расчета цепей постоянного тока.

Рис. 1

1) Метод наложения.

Для нахождения токов ветвей, создаваемых источником эдс Е₁, проводим расчет вспомогательной схемы на рис. 2, а. Эквивалентное сопротивление в данном случае

R_экв1 = R₁ + = 3,875 Ом.

Токи ветвей соответственно равны:

I₁₁= Е₁/ R_экв₁ = 15,5 A; I₁₂ = I₁₁ R₃/(R₂+ R₃) =9,6A; I₁₃ = I₁₁ – I₁₂ = 5,9 А.

Для нахождения токов ветвей, создаваемых источником эдс Е₂, проводим расчет вспомогательной схемы на рис. 2, б. Эквивалентное сопротивление R_экв2 = R₂+ = 4,4 Ом. Токи ветвей соответственно равны:

I₂₂ = Е₂/ R_экв2 = 17 А; I₂₃ = I₂₂ = 49А; I₂₁ = I₂₂ – I₂₃ = 12,1 А.

Учитывая направления токов на рис. 2, а, б, определяем искомые токи, как алгебраические суммы I₁ = I₁₁ + I₂₁ = 27,6 А; I₂ = I₁₂ + I₂₂ = 26,6 А; I₃ = I₁₃ – I₂₃ = 1 А.

2) Использование законов Кирхгофа.

Задаваясь направлениями токов, указанными на рис. 2, в, составляем уравнения для одного узла и двух контуров цепи:

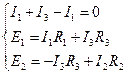или

а) б) в) г)

Рис. 2

Исключая один из токов I₃ = I₁ — I₂, получаем систему из двух уравнений:

Решением этой системы являются значения токов I₁ = 27,6 А; I₂ = 26,6 А. Ток I₃ = 1 А.

3) Метод контурных токов.

Выделим на исходной схеме два контура (рис. 2, г) и составим для них уравнения по второму закону Кирхгофа:

или

После несложных преобразований получаем систему из двух уравнений:

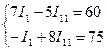
которая уже была решена в предыдущем случае, т. е. I₁ = 27,6 А и I ₁₁ = 26,6 А. В соответствии с принятыми обозначениями токов I₁ = I₁ = 27,6 А; I₂ = I₁₁ = 26,6 А; I₃ = I₁ – I₁₁ = 1 А.

4) Метод узловых напряжений.

Воспользовавшись формулой , где Y – проводимость соответствующей цепи между узлами 1 и 2, находим напряжение между узлами 1 и 2:

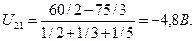
Токи ветвей соответственно равны I₁ = (E₁ — U₂₁)/R₁= 27,6 А; I₂ = (E₂ + U₂₁)/R₂ = 26,6 А; I₃ = U₂₁/R₃ = 1 А.

5) Метод эквивалентного источника.

Вначале выделим ветвь 1, заменив остальную часть цепи по отношению к ней в виде эквивалентного источника Е_х = U_x₁ и R_вн = R_в1 где

U_x1=E₁+U₁₂=E₁+E₂R₃/(R₂+R₃)= 107 B;

R_в1=R₂R₃/(R₂+R₃)= 1,875 Ом.

Следовательно, ток ветви 1 по закону Ома равен

I₁ = U_x₁/(R_B₁+R₁) = 7,6 А.

Аналогичные соотношения можно записать и для ветви 2:

U_x₂ = E₂ + U_l₂ = -Е₂ + E₁R₃/(R₁+R₃) = 117,8 В;

R_B₂= R₁R₃/(R₁+R₃) = 1,43 Oм.

Ток ветви 2равен I₂ = U_x₂/(R_B₂+R₂) = 26,6 А.

Ток ветви 3 определяется как разность токов I₃ = I₁— I₂ = 1 А.

Таким образом, для заданной схемы наиболее простым является метод узловых напряжений.

Для контроля правильности расчета можно воспользоваться формулой баланса мощностей

E₁I₁+E₂I₂=

Подставляя численные значения токов и сопротивлений резисторов, получаем 3651 = 3651.

Пример 2. Нагревательный прибор сопротивлением 24 Ом включен в сеть переменного тока с напряжением 120 В. Определить ток, мощность прибора и какое количество энергии потребляет прибор за 20 минут.

Дано: R = 24 Ом Решение: По закону Ома для участка цепи U = 120 B находим силу тока

t = 20 мин

Найти: I =? P =? W =? .

Тогда активная мощность нагревательного прибора будет определяться по формуле . Мощность нагревательного прибора находится как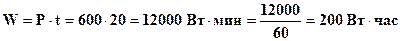

Ответ: I = 5 А, P = 600 Вт, W = 200 Вт∙час.

Пример 3. К трехфазной сети с нулевым проводом подключена несимметричная нагрузка, фазы которой характеризуются параметрами: для фазы А – R_A=0,8 Ом, X_LA = 1,2 Ом; для фазы В – R_В=0,4 Ом, X_СВ = - 2 Ом; для фазы С – R_С = 1 Ом, X_L_С = 1,8 Ом. Определить фазные и линейные токи, ток нулевого провода и коэффициенты мощности каждой фазы при их соединении звездой. Линейные напряжения сети равны 380 В.

Дано:

R_A=0,8 Ом Решение: Фазные напряжения при наличии X_LA = 1,2 Ом уравнительного нулевого провода, представле R_В=0,4 Ом нные в комплексном виде равны: U_фА = U_л/ =

X_СВ = - 2 Ом = 220 В; U_фВ = 220 е^-^j¹²⁰ В; U_фС = 220 е^j¹²⁰ В

R_С = 1 Ом (смотри [8, c 70]). Сопротивления фаз нагрузки X_L_С = 1,8 Ом в соответствии с условием задачи:

U_л = 380 В Z_A = 1,44 e^-^j⁴¹ Ом; Z_В = 2 e^-^j^78,7 Ом; Z_С = 2 e^j⁶¹ Ом.

f = 50 Гц Фазные токи определяются из соотношений

I_фА = 153 e^-^j⁵⁶ А; I_фС = 110 e^-^j⁴¹ А; I_фА = 110 e^j⁵⁹ А.

Найти: I_ф =?; I_л=?; I₀ =?; Линейные токи в этой схеме равны фазным, а

cos φ =? ток нулевого провода определяется суммой:

I₀ = I_А+I_В+I_С = 85-j 127 +82,6- j 72,6+56,6+ j 92,3 = 224,2- j107,3 = 284 e^j25,6 А.

Коэффициенты мощности определяются углами сдвига фаз токов и напряжений, т.е. cos φ_A = 0,555; cos φ_B = 0,196; cos φ_C = 0,485.

Пример 4. Последовательно соединенные катушка с активным сопротивлением R Ом и индуктивностью L Гн и конденсатор с емкостью C мкФ включены в сеть U В, f Гц. Определить ток в цепи, напряжение на катушке и на конденсаторе, активную и реактивную мощности, угол сдвига фаз между напряжением и током в цепи.

Дано:

L = 0,07 = 70*10^-3 Гн Решение: 1. На основе условия задачи со- R = 8 Ом ставим схему цепи

С = 122 мкФ = 122*10^-6 Ф

U = 120 В

f = 50 Гц

Найти: I =?; U_L=?; U_C=?;

P=?; Q=?; φ =?