ФИЗИЧЕСКАЯ МОДЕЛЬ И СТАТИЧЕСКИЕ
ВОЛЬТ-АМПЕРНЫЕ ХАРАКТЕРИСТИКИ
ТРАНЗИСТОРОВ
В связи со сложностью процессов постоянные и переменные составляющие токов (напряжений) в транзисторах анализируются раздельно [14]. При расчете сравнительно больших постоянных составляющих используется нелинейная физическая модель Молла-Эберса (рис.2.1, а) и соответствующие уравнения:
, (2.1)
. (2.2)
В модели учтена асимметрия транзистора: при нормальном включении транзистора (когда к коллекторному переходу приложено обратное напряжение, а к эмиттерному – прямое) через переходы протекают ток эмиттера I э и ток коллектора 
, причем коэффициент передачи эмиттерного тока 
, что связано с частичной рекомбинацией инжектированных эмиттером дырок в базе. Кроме того, через коллекторный переход протекает тепловой ток 
, зависящий от обратного напряжения U к. При U к = 0 ток I 2 обнуляется.
Здесь 
– тепловой ток эмиттерного перехода при U э и оборванном коллекторе; 
– температурный потенциал перехода (при 
имеем 
= 0,25 B); 
Дж/град – постоянная Больцмана; 
Кл – элементарный заряд, I ко – обратный ток коллекторного перехода.
По выражениям (2.1), (2.2) можно построить семейство коллекторных (рис. 2.1, б) и эмиттерных (рис. 2.1, в) вольт-амперных характеристик (ВАХ). Первый квадрант рис. 2.1, б соответствует активному режиму транзистора типа p-n-p при 
, а второй квадрант – режиму насыщения 
. Для активного режима 
и формулы (2.1), (2.2) упрощаются
, (2.3)
.
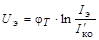Реальные статические характеристики I к(U к) имеют небольшой наклон, который резко увеличивается, когда напряжение 
приближается к напряжению лавинного пробоя (пунктирные линии на рис. 2.1, б). Расстояние между кривыми при больших токах уменьшается из-за уменьшения коэффициента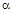 
. При нагреве транзистора кривые смещаются вверх из-за роста тока I ко.
Эмиттерные ВАХ слабо зависят от коллекторного напряжения, т.е. расположены на малом расстоянии друг от друга (рис. 2.1, в). При нагреве транзистора кривые смещаются влево. При одинаковом эмиттерном токе напряжение 
для кремниевых транзисторов на 0,3¸0,4 В больше, чем для германиевых. Отличие транзисторной характеристики от диодной заключается в том, что напряжение включает в себя сравнительно малое слагаемое 
(
= 50¸200 Ом – сопротивление пассивной области базы).
Для схемы с общим эмиттером (ОЭ) задаются значения тока базы и коллекторного напряжения. Поэтому в качестве ВАХ БТ рассматриваются функции I к(I б, U кэ) и 
, называемые соответственно семейством выходных (коллекторных) характеристик (рис. 2.1, г) и семейством входных (базовых) характеристик (рис. 2.1, д). Основной особенностью выходных ВАХ при данном включении транзистора является то, что они полностью расположены в первом квадранте. Действительно 
, т.е. кривые ОЭ получаются путем сдвига кривых схемы с общей базой (ОБ) на величину 
, возрастающую с увеличением тока 
. Наклон характеристик в схеме ОЭ значительно больше, а дифференциальное сопротивление 
, характеризующее этот наклон, эначительно меньше, чем в схеме ОБ. Это объясняется тем, что приращение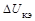 
частично падает на эмиттерном переходе, т.е. вызывает приращение 
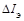и дополнительное приращение тока I к. В предпробойной области наклон ВАХ быстро возрастает, причем напряжение лавинного пробоя коллекторного перехода
в схеме ОЭ меньше, чем в схеме ОБ.
Кривые коллекторных характеристик для включения ОЭ менее регулярны, чем для схемы ОБ, они заметно сгущаются при увеличении тока I к. За счет рекомбинации носителей в эмиттерном переходе входная характеристика транзистора имеет меньший наклон по сравнению с ВАХ идеального диода. Величина этого отклонения зависит от качества эмиттерного перехода, которое характеризуется m -фактором:
где m =1,2 
2; 
2.1. МАЛОСИГНАЛЬНЫЕ ЭКВИВАЛЕНТНЫЕ СХЕМЫ
И ПАРАМЕТРЫ АКТИВНЫХ ЭЛЕМЕНТОВ
Для анализа переменных составляющих токов (напряжений) в усилительных элементах нелинейная модель Молла-Эберса непригодна, так как связь между малыми приращениями токов и напряжений определяется не функциями I (U), а их производными. Сложные процессы в транзисторах и лампах практически невозможно описать с помощью аналитических выражений. В этом случае применяется предложенная Джиаколетто малосигнальная модель (эквивалентная схема) из линейных элементов. Элементы такой схемы соответствуют комплексным сопротивлениям переходов транзисторов или междуэлектродных промежутков ламп. Таким образом, процессы в активном элементе (AЭ)
с достаточной точностью описываются в некотором диапазоне частот (f < fТ, где fТ – предельная частота усиления АЭ). Составленные для эквивалентной схемы уравнения Кирхгофа позволяют найти коэффициенты передачи, входные и выходные проводимости АЭ.
Эквивалентные схемы БТ для включения ОБ и ОЭ показаны на рис. 2.2 и 2.3. Они содержат следующие элементы:
– дифференциальный коэффициент передачи по току
в схеме с ОБ (практически мало отличается от интегрального коэффициента 
);
50¸200 Ом – объемное сопротивление базы;
– дифференциальное сопротивление эмиттерного перехода;
|
|
|
Рис. 2.2
|
|
|
|
|
Рис. 2.3
– температурный потенциал эмиттерного перехода. При Т = 300 К 
= 0,025 B;
С бэ – емкость эмиттерного перехода (сумма конструктивной С кон
и диффузионной С диф емкостей, С диф = C (U э);
– дифференциальное сопротивление коллекторного перехода, обусловленное эффектом Эрли (влиянием напряжения U к на ширину коллекторного перехода, на ширину базы и соответственно на основные параметры транзистора);
С к – емкость коллекторного перехода (при обратном смещении коллекторного перехода С к уменьшается с увеличением напряжения U к, что выгодно при работе на ВЧ);
– эквивалентная емкость коллекторного перехода для схемы ОЭ;
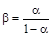– дифференциальный коэффициент передачи по току для схемы ОЭ;
– сопротивление коллекторного перехода для схемы ОЭ (
, так как наклон пологих участков входных ВАХ при включении с ОЭ значительно больше, чем для схемы ОБ с практически горизонтальными характеристиками).
С помощью рис. 2.2 и 2.3 можно показать основное отличие схем ОБ и ОЭ. Запишем уравнение Кирхгофа для рис. 2.2 в диапазоне низких частот (когда влиянием емкости С бэ можно пренебречь)
.
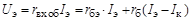Соответственно
,
где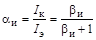 
– интегральный коэффициент передачи тока,
.
Аналогично для cxeмы ОЭ (рис. 2.3):
,
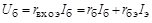отсюда получаем
.
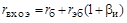С учетом соотношения
видно, что за счет усилительных свойств транзистора в схеме ОБ вклад 
во входное сопротивление уменьшается в (
) раз. В схеме ОЭ в () раз увеличивается вклад сопротивления 
.
Таким образом, при 
,
т.е. входное сопротивление БТ в схеме ОЭ намного превышает его входное сопротивление при включении с ОБ.
ПАРАМЕТРЫ АКТИВНЫХ ЭЛЕМЕНТОВ
КАК ЧЕТЫРЕХПОЛЮСНИКОВ
Активные элементы, имеющие два входных и два выходных зажима, можно рассматривать как четырехполюсник. Четырехполюсники описываются различными системами параметров: | Y |, | Z |, | H |, которые отличаются режимом иэмерения. Чаще всего для активных элементов используются | Y |-параметры (они определяются в режиме короткого замыкания) и | Z |-параметры (определяются в режиме холостого хода). На практике легче обеспечить режим короткого эамыкания, поэтому | Y |-параметры более распространены.
Для упрощения анализа работы усилительных каскадов с помощью y -параметров преобразуют эквивалентную схему БТ для основного включения с ОЭ (рис. 2.3) в эквивалентную схему с разделением цепи обратной передачи (рис. 3.17, а)
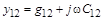
и выходной цепи
.
Если напряжения считать аргументами, то свойства четырехполюсника полностью характеризуются системой уравнений, которые связывают входные и выходные величины через | Y |-параметры
(рис. 2.4, а):
, (2.4)
т.е.
при 
; 
при 
;
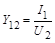при ; 
при .
Это усредненные параметры для определенного участка ВАХ. Они представляют собой:
– входная проводимость; 
– обратная проводимость;
– прямая проводимость; 
– выходная проводимость.
Рис. 2.4
В связи с нелинейностью ВАХ усилительных элементов приращения токов и напряжений желательно задавать в соответствии с амплитудными значениями реального сигнала в окрестностях выбранной рабочей точки транзистора (U 1, U 2)
.
Это дифференциальные параметры, которые привязаны к конкретной рабочей точке ВАХ. Комплексные параметры содержат активную и реактивную составляющие
.
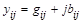Значения активных проводимостей находятся графически в окрестностях выбранной рабочей точки ВАХ, реактивные проводимости 
(на умеренно высоких частотах, как правило, емкостные) измеряются экспериментально и приводятся в справочных данных.
По входной характеристике (рис. 2.4, б) можно определить величину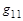 
для биполярного транзистора в рабочей точке (РТ) с координатами I б0, U бэ0 :
.
По выходной характеристике (рис. 2.4, в) находится выходная проводимость
.
По входной характеристике и семейству выходных характеристик
(рис. 2.4, г, д) определяется прямая проводимость, равная крутизне сквозной (проходной) характеристики усилительного элемента в рабочей точке I к0, U кэ0 ,
.
Нагрузочная прямая по постоянному току соединяет точки U кэ = Е п,
I к = Е п/ R н и строится под углом jн (см. п. 3.5.2).
Зная | y |-параметры, можно определить свойства нагруженного четырехполюсника, т.е. коэффициент усиления К, коэффициент передачи в обратном направлении 
, входную и выходную проводимости 
. Пусть в цепях усилителя токи текут по направлению стрелок, а для напряжений стрелки направлены к контакту с большим потенциалом (рис. 2.4, а)
,
тогда из второго уравнения системы (2.4) получаем:
. (2.5)
Аналогично находим коэффициент передачи в обратном направлении согласно (2.5)
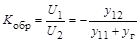. (2.6)
Преобразование второго уравнения дает выражение для выходной проводимости четырехполюсника:
|
= 
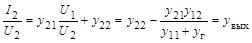. (2.7)
С учетом (2.5) можно записать
что позволяет найти входную проводимость четырехполюсника
|
|
|
. (2.8)
| H |-параметры (смешанные) входят в систему уравнений:
, (2.9)
т.е.
где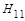 
, 
– определяются в режиме короткого замыкания вы-
хода; 
, 
– определяются в режиме холостого хода на вхо-
де; 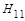– входное сопротивление; – входная проводимость.
При этом , – безразмерные параметры; – коэффициент передачи четырехполюсника по току; – внутренняя ОС по напряжению.
Величины элементов матрицы | h | измеряются тоже как дифференциальные параметры в точке ВАХ:
.
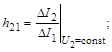
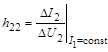Связь | y |-параметров и | h |-параметров записывается в виде матрицы
На СВЧ сложно реализовать режим холостого хода, поэтому к четырехполюснику подключают резисторы определенной величины и измеряют параметры рассеяния (| S |-параметры). Это преобразование допустимо и корректно со стороны источника сигнала, так как 
, и также со стороны нагрузки, так как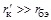 
; 
, т.е. источник выходного тока транзистора 
можно считать включенным параллельно нагрузке (выводы "К", "Э" рис. 2.3, a).
Для БТ комплексные проводимости (y -параметры) удобно представлять в виде комбинации активной и реактивной (емкостной) составляющих:
Здесь
|
|
|
|
|
|
Mодуль и фаза прямой проводимости определяются выражениями:
Крутизна проходной характеристики находится как
Постоянная времени входной цепи транзистора в схеме ОЭ
и определяет граничную частоту 
, на которой модуль прово-
димости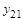 
снижается на 3 dB относительно своего максимального значения S. На предельной частоте 
транзистор теряет усилительные свойства 
.
Для умеренно высоких частот (когда пролетные эффекты в базе можно не учитывать) 
, и формулы упрощаются:
|
