Биполярный транзистор может включаться по схеме с общей базой ОБ, общим эмиттером ОЭ и общим коллектором ОК (рис. 25).
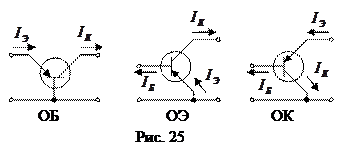При любых способах включения физические процессы, происходящие в транзисторе, одинаковы. Изменение схемы включения приводит к смене входных и выходных величин и параметров транзистора. Так, при включении транзистора по схеме ОБ входными величинами являются 
и 
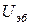, а выходным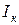и – 
и 
. При включении по схеме ОЭ входными величинами являются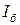 
и 
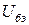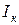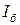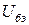, а выходными – и . В схеме ОК входные величины и , выходные - и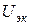 
. Входные величины обозначаются индексом “1”, а выходные - “2”.
Свойства биполярного транзистора могут быть представлены четырьмя семействами характеристик:
1. входных: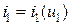 
при 
;
2. выходных: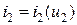 
при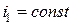 
;
3. передачи тока: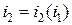 
при ;
4. обратной связ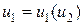и: 
при ;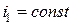
Чаще всего используются семейства входных и выходных характеристик. Семейства статических входных и выходных характеристик для схемы ОЭ показаны на рис. 26. Эти характеристики могут быть
использованы для определения параметров транзистора.
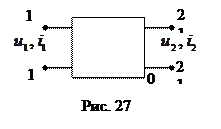Транзистора можно представить в виде четырёхполюсника (рис. 27) – устройства, имеющего два входных и два выходных зажима. В общем случае входные 
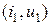и выходные 
напряжения и токи связаны нелинейными функциональными зависимостями. Из четырёх величин любые две могут быть выбраны в качестве независимых переменных, а две другие – рассматриваются как функции этих переменных. В качестве независимых переменных могут быть выбраны, например, напряжение на входе и выходе четырёхполюсника. Тогда 
, 
представляют собой нелинейные функции. Полные дифференциалы этих функций имеют вид:
(1)
Пусть переменные составляющие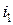 
, 
, 
, 
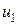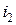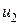столь малой амплитуды, что в пределах их изменения нелинейные функции можно аппроксимировать линейными зависимостями. Тогда в такой области частные производные (1) будут постоянными величинами, полные дифференциалы токов и напряжений можно заменить комплексными амплитудами соответствующих переменных. Тогда из (1) следует, что
(2)
Выясним физический смысл частных производных. По определению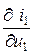 
находится при 
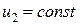, что означает отсутствие переменного напряжения на выходе четырёхполюсника. Условие 
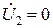выполняется только при коротком замыкании (К. З.) выхода четырёхполюсника по переменной составляющей.
Тогда 
при К. З. На выходе четырёхполюсника по переменной составляющей.
- комплексная величина.
, представляет собой проводимость четырёхполюсника при коротком замыкании на выходе.
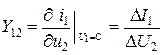при 
- К. З. на входе характеризует обратную проходную проводимость.
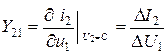при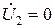 
- К. З. на выходе характеризует прямую проходную проводимость.
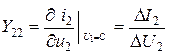при - К. З. на входе характеризует выходную проводимость.
Специфика электронного прибора представлена в уравнениях (2) параметрами Yik, которые носят название Y-параметров (параметры проводимости) и зависят от режима работы электронного прибора.
Режим К. З. по переменной составляющей тока осуществляется включением параллельно входным “11” и выходным “22” зажимам конденсаторов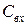 
и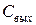 
(рис. 28) достаточно большой ёмкости, чтобы выполнялось неравенство: 
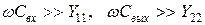, где 
- частота воздействующего на прибор переменного напряжения. , 
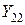– входные и выходные проводимости.
Режим К. З. выходной цепи не представляет труда осуществить, т. к. выходная проводимость Y22 транзистора мала. Создание режима К. З. входной цепи затруднительно из-за большой входной проводимости . При большом значении практически не удаётся создать режим К. З. на входе, особенно в области низких частот. Система дифференциальных уравнений (2) незамкнута: два параметра и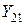 
можно определить, а два 
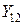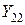, – нельзя.
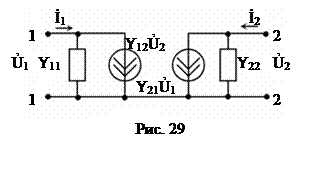
Система уравнений (2) может быть использована для построения схемы замещения, представляющей электронный прибор как четырёхполюсник (рис. 29). В схеме замещения (рис. 29) зависимые источники представлены в виде источников тока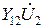 
и 
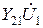. В соответствии с первым уравнением (2) входной ток 
равен сумме двух слагаемых: первое слагаемое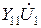 
является током, текущем через проводимость под действием входного напряжения с амплитудой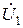 
; второе слагаемое 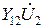, учитывающее влияние выходного напряжения на входной ток, отражается в схеме замещения источником тока 
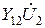. Аналогично, на основе второго уравнения (2) строится правая часть схемы (рис. 2а), отражающая выходную цепь четырёхполюсника.
Если в качестве независимых переменных выбрать входные и выходные токи, тогда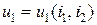 
, 
представляют собой нелинейные функции.
Полные дифференциалы этих функций имеют вид:
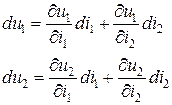(3)
Если в уравнениях (3) переменные составляющие столь малой амплитуды, что в пределах их изменение нелинейные функции можно аппроксимировать линейными зависимостями. Тогда полные дифференциалы токов и напряжений можно заменить комплексными амплитудами соответствующих переменных. При этом связь между комплексными амплитудами тока и напряжений выражается системой уравнений, носящих название системы с Z-параметрами.
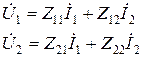(4)
Физический смысл Z-параметров:
- характеризует входное сопротивление при холостом ходе (Х. Х.) на входных зажимах транзистора.
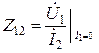- обратное проходное сопротивление при холостом ходе на входе.
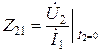- прямое проходное сопротивление при Х. Х. на выходе.
- выходное сопротивление при Х. Х. на входе.
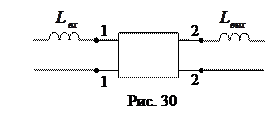Z-параметры – параметры сопротивления зависят от режима работы транзистора.
Режим Х. Х. по переменной составляющей тока осуществляется включением индуктивносте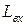й 
и 
последовательно с входными и выходными зажимами четырёхполюсника (рис.30), чтобы выполнялось неравенство: 
.
Так как входное сопротивление Z11 мало, то режим Х. Х. Входной цепи осуществить легко. Режим Х. Х. выходной цепи практически осуществить нельзя из-за большого выходного сопротивления Z22 (порядка 105 Ом). Следовательно, параметры Z11 и Z21, определяемые при Х. Х. на выходных зажимах транзистора, определить нельзя.
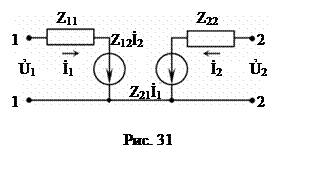
Схема замещения, описываемая системой уравнений (4), представлена на рис. 31. В этой схеме зависимые источники представлены в виде источников напряжения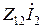 
и 
. В соответствии с первым уравнением (4) входное напряжение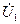 
равно сумме напряжений на входном сопротивлении 
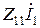и напряжении 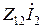, учитывающего влияние выходного тока 
на входное напряжение, отображается в схеме замещение источником напряжения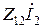 
. Аналогично, на основе второго уравнения (4) строится правая часть схемы замещения.
Чтобы избежать трудностей, возникающих при определении Y- и Z-параметров, в качестве независимых переменных выбрали входной ток и выходное напряжение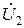 
. Связь между комплексными амплитудами тока и напряжений выражается системой уравнений, носящих название Н-параметров (смешанных или гибридных параметров):
(5)
где:
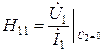- входное сопротивление при К. З. на выходе транзистора.
- коэффициент обратной связи по напряжению при Х. Х. на входе транзистора.
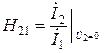- коэффициент передачи тока при К. З. выходных зажимах.
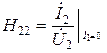- выходная проводимость при Х. Х. на входных зажимах.
Н-параметры определяются в режиме К. З. на выходе транзистора и режиме Х.Х. на входе, что легко может быть реализовано. Простота измерений Н-параметров составляет их преимущество.
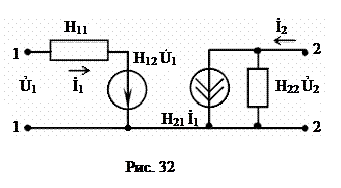
Схема замещения, описываемая уравнениями (5) представлена на рис. 32.
Численные значения параметров зависят от схемы включения транзистора как четырёхполюсника (ОБ, ОЭ и ОК), поэтому кроме цифровых индексов используются буквенные индексы, например Н11б, Н11э, Н11к и т. д.
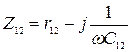Параметры транзистора в общем случае являются комплексной величиной, например: , или 
, или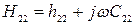 
, где первое слагаемое представляет собой активную составляющую:
g11 – активная составляющая входной проводимости;
r12 – активная составляющая обратного проходного сопротивления;
h22 – активная составляющая выходной проводимости.
Второе слагаемое представляет реактивную составляющую. Так как межэлектродные ёмкости транзистора малы, то ими можно пренебречь в области низких частот.
