Основные законы и тождества алгебры логики

 

Для преобразования функции используется ряд законов и тождеств, основные из которых приведены ниже.

Теоремы алгебры Буля:

– основные правила:

 

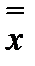1) х + 0 = х, 2) х + 1 = 1, 3) х + х = х, 4) + х = 1, 5) = х,

6) х × 1 = х, 7) х × 0 = 0, 8) х × х = х, 9) х × = 0.

 

 

3.5. Минимизация ФАЛ методом карт Карно

 

Под минимизацией ФАЛ понимается преобразование ее алгебраического выражения с целью наиболее простого представления функции. В инженерной практики для минимизации наиболее широко используются следующие методы: метод последовательного упрощения, основанный на использовании законов и тождеств АЛ; метод, основанный на применении карт Карно; метод Квайна-Мак-Класски.

При использовании метода карт Карно производится накрытие с помощью правильных конфигураций, содержащих нули или единицы. Правильными конфигурациями на карте Карно для ФАЛ от n- переменных являются все прямоугольники (горизонтальные, вертикальные, квадраты), имеющие площадь 2 ^n-i (i = 0, 1, 2, …, n).

При накрытии ФАЛ стремятся, чтобы число накрытий на карте было минимально, а площадь, накрываемая каждой правильной конфигурацией, – максимальна. Конфигурации могут перекрываться, накладываться друг на друга. При выборе накрытия возможно объединение крайних полей, расположенных на противоположных сторонах карты, в горизонтальном и вертикальном направлениях. Принцип минимизации заключается в объединении соседних полей карты в пределах правильных конфигураций. При нахождении минимальной формы ФАЛ выписываются переменные, не изменяющие своего значения в пределах правильной конфигурации.

При объединении полей, в которых записаны единицы, ФАЛ выписывается в ДНФ, т.е. в виде дизъюнкции произведений переменных, неизменных в пределах каждой конфигурации накрытия. При объединении полей, содержащих нули, ФАЛ записывается в КНФ, т.е. в виде произведений дизъюнкций инверсных значений переменных, не меняющихся при переходе с одного поля конфигурации на другое. Примеры минимизации нескольких ФАЛ методом Карт Карно схемы на рис. 3.1 представлены в табл. 3.5, табл. 3.4 – исходная таблица трех переменных.

 

Х1

Х2

Х0

Х 0

Х1

Х 2

Х2

Таблица 3.4

 

 

 

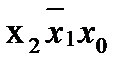
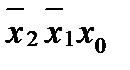
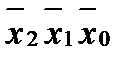
В полученной таблице заменяем существующие в ФАЛ наборы единицами, несуществующие нулями, получаем следующую таблицу:

 

Таблица 3.5

1

 

Записываем пересечения множеств, полностью описывающих прямоугольные выделенные области. То есть получаем .

Для 4 переменных общая таблица 3.6, для заданной ФАЛ – таблица 3.7:

Таблица 3.6

х 1

х 0

х3

х 2

 

 

 

 

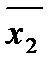
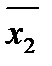
Таблица 3.7

Получаем: 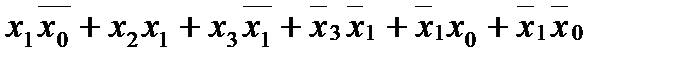как объединение множеств.

1. Кубические комплексы, рис 3.3.

 

 

Рис 3.3

 

Выделяем ребра, которые целиком обозначены существующими в ФАЛ наборами. Записываем соответствующий 0-куб, включающий в себя покрытия ребер, где несовпадающее значение обозначается «_»: ((_,1,1),(1,_,1),(1,1,_)), то есть можно записать .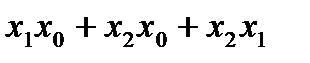

Если точками ограничена вся грань, то она будет описываться только одной переменной, которая совпадает во всех четырех наборах, например, передняя грань полностью описывается переменной .

 

3.6. Минимизация ФАЛ

методом Квайна-Мак-Класски

 

Данный метод основывается на задании входящих в ДСНФ функции элементарных произведений в виде двоичных чисел, называемых номерами соответствующих наборов. Кроме номера каждому произведению присваивается определенный индекс, под которым понимается число единиц в двоичном представлении данного набора. Например:

В результате реализации данного метода ФАЛ разлагается на простые импликанты. Под простой импликантой функции понимается всякое элементарное произведение, принимающее единичное значение на всех наборах аргументов, что и исходная ФАЛ, при исключении из которого хотя бы одного аргумента уже не будет выполняться данное условие.

Алгоритм Квайна-Мак-Класски формулируется следующим образом: для того чтобы два числа m и n являлись номерами двух склеивающихся между собой наборов, необходимо и достаточно, чтобы индексы данных чисел отличались на единицу, сами числа отличались на степень числа два и число с большим индексом было больше числа с меньшим индексом.

Реализацию алгоритма рассмотрим на примере минимизации ФАЛ:

 

.

 

На первом этапе минимизации определяем номера и индексы каждого набора, записывая ФАЛ в виде:

,.

 

Группируем наборы, располагая их в порядке возрастания индексов.

Минимизация ФАЛ методом Квайна-Мак-Класски.

Таблица 3.8

 

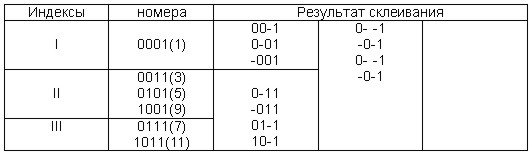
На следующем этапе производим склеивание различных наборов, руководствуясь приведенной выше формулировкой алгоритма.

Подлежащие склеиванию пары чисел указаны стрелками. При склеивании не совпадающие в числах разряды отмечаются прочерками. Например, склеивание чисел 0001 и 0011 дает число 00-1. Результат склеивания выписывается в следующий столбец таблицы 3.8, так же разделяемый на строки с индексами, отличающимися на единицу. После склеивания всех групп первого столбца таблицы переходят ко второму столбцу, вписывая результат склеивания в третий столбец. При объединении наборов второго и последующих столбцов таблицы возможно склевать только числа, содержащие прочерки в одноименных разрядах. Склеивание продолжается до тех пор, пока образование нового столбца станет невозможным.

По окончании склеивания приступают к построению импликантной таблицы (табл. 3.9), записывая в нее в качестве простых импликант наборы, содержащиеся в последнем столбце табл. 3.8. В качестве простых импликант в табл. 3.9 также вписываются наборы из других столбцов табл. 3.8, не принимавшие участия в склеивании. Если импликанта, содержащаяся в I-й строке таблицы, составляет некоторую часть конституенты I-го столбца на пересечении I-й строки и I-го столбца, ставится символ*. С целью получения минимальной формы ФАЛ из табл. 3.9 необходимо выбрать минимальное число строк, чтобы для каждого столбца среди выбранных строк нашлась хотя бы одна, содержащая в этом столбце символ*.

 

 

Таблица 3.9

 

Импликантная таблица минимизируемой ФАЛ.

Полученная после минимизации ФАЛ записывается в следующем виде: