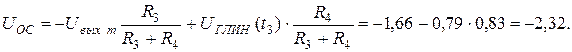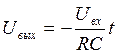Если напряжение на входе ОУ постоянное, то на его выходе формируется линейно изменяющееся напряжение

,

причем знак приращения обратный знаку входного напряжения.

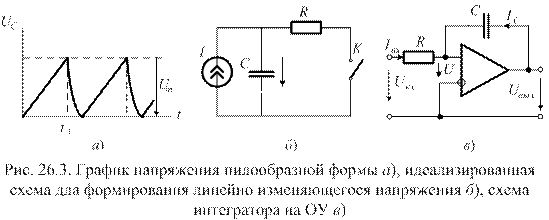
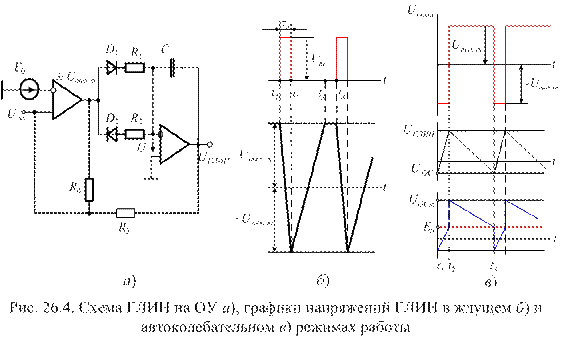
Схема ГЛИН с внешним управлением приведена на рис. 26.4, а. На рис. 26.4, б приведены диаграммы напряжений, поясняющие его работу.

Схема состоит из компаратора и интегратора. Допустим, что в исходном состоянии напряжение на входе отсутствует: U_вх = 0. Под воздействием напряжения Е₀ компаратор находится в состоянии отрицательного насыщения – U_вых.m. Это напряжение поступает на вход интегратора и вызывает заряд конденсатора С до напряжения .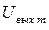

Пусть в момент времени t ₁ на прямой вход поступает прямоугольный импульс, амплитуда которого U_m > E ₀. Компаратор переходит в положительное насыщение, т. е. напряжение на его выходе 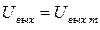. Это напряжение является входным для интегратора. Открывается диод D₁, начинается перезаряд конденсатора С до 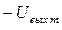. Напряжение U_ГЛИН убывает по линейному закону в соответствии с выражением:

 

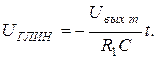
По окончании импульса компаратор регенеративно переходит в отрицательное насыщение (под воздействием Е ₀). Диод D₁ закрывается. Открывается диод D₂. Начинается перезаряд конденсатора С до напряжения 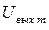. Напряжение U_ГЛИН возрастает по линейному закону

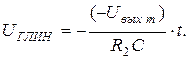
Максимального значения оно достигает за время t = R₂C. Если пауза 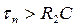, то ГЛИН переходит в устойчивое состояние (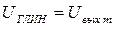) до поступления следующего импульса управления.

Кроме рассмотренной схемы, часто применяются ГЛИН в автоколебательном режиме. Чтобы получить такой ГЛИН, достаточно в схему рис. 26.4, а ввести ОС – R ₃, R ₄ на прямой вход компаратора с выходов компаратора и интегратора (пунктирная линия на рис. 26.4, а). Напряжение обратной связи U_ОС будет определяться напряжением на выходе компаратора 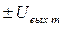и напряжением на выходе интегратора U_ГЛИН. На рис. 26.4, в приведены графики напряжений, поясняющие работу генератора.

Пусть в момент времени t ₁ = 0 компаратор перешел в состояние отрицательного насыщения. Его 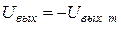. Открывается диод D ₂, и на интеграторе начинается формирование линейно нарастающего напряжения U_ГЛИН. Напряжение обратной связи U_ОС найдем методом суперпозиции:

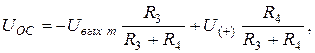(26.9)

где 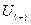- линейно нарастающее напряжение U_ГЛИН.

Видим, что U_ОС также линейно нарастает. В момент времени t ₂ наступает равенство U_OC = Е₀. Компаратор переключается, напряжение его на выходе скачком изменяется до 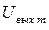. Напряжение интегратора скачком измениться не может. Поэтому напряжение обратной связи скачком увеличивается до U_OCm, причем

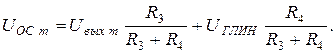(26.10)

Напряжением 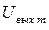открывается диод D₁. На интеграторе начинается формирование линейно падающего напряжения. Напряжение U_OC также

линейно убывает и в момент t ₃ принимает значение:

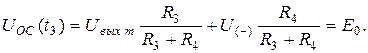
Компаратор вновь переключается, и далее процесс периодически повторяется.

Рассмотрим пример.

Пусть в схеме компаратора R ₃ = 10 кОм; R ₄ = 50 кОм; Е ₀ = 1 В; 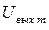= ±10 В.

Определим U_ГЛИН и U_ОС в моменты времени t ₁; t ₂; t ₃.

1. В момент времени t ₁ включается питание. Напряжение на выходе компаратора:

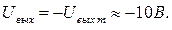
Конденсатор С до включения питания был разряжен. Напряжение U_C = 0 и скачком измениться не может. Значит, 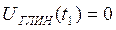, и, в соответствии с (16.13),

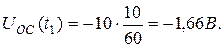
2. Для момента времени t ₂:

.

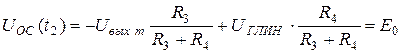Отсюда определим U_ГЛИН

.

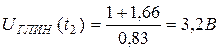Найдем значение сразу после переключения, когда значение , а U_ГЛИН еще не изменилось:

.

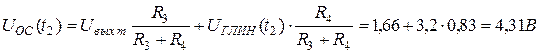3. Для момента времени t ₃:

Напряжение на выходе компаратора 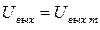. Напряжение обратной связи U_OC определяется выражением:

.

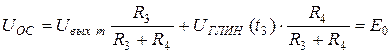Здесь U_ГЛИН (t ₃) – минимальное. Определим это значение:

.

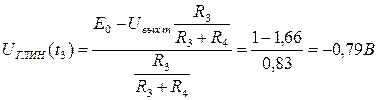Определим величину напряжения U_ОС (t ₃) сразу после переключения, когда значение 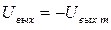, а U_ГЛИН (t ₃) = - 0,79 В.