Го и 2-го порядка. Дифференциал функции.
3.1. Вычислить:
1) значения F(2,3), F(1,2), F(2,1), F(a,0), F(0,a), если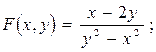 
2) значения F(2,4), F(4,2), F(1,a), если 
3.2. Найти области определения функций:
1) 
2) 
3) 
4) 
5) 
6) 
7) 
3.3. Построить несколько линий уровня функций:
1) z=xy; 2) z=y-x2; 3) z= 
4) z=ln(x2+y2); 5) z= 
Найти частные производные 1-го порядка функции:
3.4. z=x2-2xy-5y3. 3.5. z=2x3+3x2y-y+5.
3.6. z= e 
. 3.7. z=ln(x2+y2).
3.8. z= 
. 3.9. z= 
.
3.10. z= xy. 3.11. z=x2exy.
3.12. z= arctg(
). 3.13. z= arcsin .
Найти дифференциал 1-го порядка функции:
3.14. z= 
3.15. z=ln(
).
3.16. z= 
3.17. z=sin .
3.18. z= arctg 
. 3.19. z=y arcsin 
.
3.20. Доказать:
1) если 
, то 
2) если 
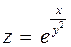, то 
.
3.21. Доказать:
1) если 
, то 
;
2) если 
, то 
.
Найти дифференциал 1-го порядка функции:
3.22. z= 
в точке (3;4).
3.23. z= ex+2y в точке (-2;1).
3.24. z= x siny в точке (3; 
).
3.25. z= ln(x+y2) в точке (-3;2).
3.26. Вычислить dz и 
z для функции z=ху при х=5, у=4, х=0,1,
у=-0,2.
3.27. Вычислить dz и z для функции z=ln(x2+y2), когда х изменяется от 2 до 2,1, а у - от 1 до 0,9.
3.28. Подсчитать приближенно приращение функции:
1) z=arctg 
если х изменяется от 2 до 2,1, а у- от 3 до 2,5;
2) z=arcsin если х изменяется от 5 до 4,5, а у- от 3 до 3,3.
Найти частные производные 2-го порядка:
3.29. z= x2-2xy+5y2. 3.30. z= 
.
3.31. z= 
. 3.32. z= ln(x2-y2).
3.33. Проверить, что 
для функций:
3.34. Найти частные производные 3-го порядка для функций:
1) z=2x3+xy2-y3+y2-x; 2) z= 
.
3.2. Производная по направлению и градиент функции.
3.35. Найти grad z(x,y) для функции:
1) 
2) 
3) 
; 4) 
3.36. Построить линии уровня и grad z в точке А(1;2) для функций:
1) z=4-x2-y2; 2) z=x2-y;
3) z=2x+y-3; 4) z= .
3.37. Найти 
, если
1) z=ln(x+y) 
arctgy, 
;
2) z=e 
+xy, 
;
3) z= 
, 
;
4) z=x3+xy2-y3, 
.
3.38. Найти производную функции z=ln(ex+ey) в точке (0;0) в направлении 
и в направлении градиента.
3.39. Найти производную функции z(x,y) в точке (1;2) в направлении 
и в направлении градиента, если:
1) z=4-x2-y2; 2) z=x2-y;
3) z= 2x+y-3; 4) z=
(cм. задачу 3.36).
3.3. Экстремум функции двух переменных.
Найти экстремумы функции:
3.40. z= 3x2 +xy+2y2+4x-7y+15.
3.41. z= -x2+2xy-2y2 +2x+20.
3.42. z= 5x2 +2xy - y2-4x-8y+10.
3.43. z= x3 +8y3 -6xy +1.
3.44. z= 2x3 -xy2 +5x2+y2.
3.45. z= 
.
3.46. z= e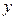 
(
).
Найти наибольшее и наименьшее значения функции:
3.47. z= -2xy -2x+y при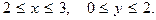 
3.48. z= x2-2xy +x+y+5 при 
3.49. z= x2-xy +y2 -x-y+2 при 
3.50. z= sin (x+y)+sinx+siny при 
Найти экстремумы функции:
3.51. 
при х+у=2.
3.52. z=x+y при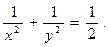 
3.53. z=xy при условии, что х2+у2=2.
Раздел II. Интегральное исчисление.
Дифференциальные уравнения. Ряды.
Тема 4. Интегралы.
4.1. Понятие неопределенного интеграла.
Вычисление неопределенных интегралов.
4.1. Проверить, что:
Вычислить интегралы:
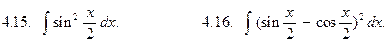
Применяя метод замены переменных, вычислить интегралы:
С помощью метода интегрирования по частям вычислить интегралы:
При вычислении интеграла воспользоваться тем, что 
Вычислить интегралы, используя формулы:
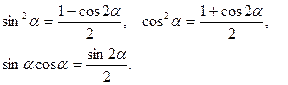
В примерах 4.92 - 4.95 применить подстановку
тогда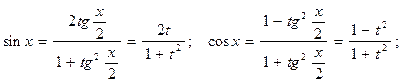 
Вычислить интегралы:
Понятие определенного интеграла. Вычисление определенного интеграла.
4.117. Составлением интегральных сумм и переходом к пределу найти интегралы:
4. 118. Вычислить интегральную сумму S5 для интеграла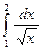 
, разбив отрезок [1;2] на пять равных частей и взяв в каждой части ее середину. Сравнить с точным значением интеграла.
4.119. Выполнить задание предыдущей задачи для интеграла 
Вычислить:
4.120.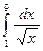 
4.121. 
4.122. 
4.123. 
4.124. 
4.125. 
4.126. 
4.127. 
4.128. 
4.129. 
4.130. 
4.131. 
4.132. 
4.133. 
4.134. 
4.135.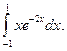 
4.136.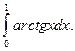 
4.137. 
