Найти точки разрыва функции

1.81. Исследовать на непрерывность функцию  на отрезке:
на отрезке:

1.82. Исследовать на непрерывность функцию 
на отрезке:

Определить характер точек разрыва:

Тема 2. Дифференциальное исчисление функций одной переменной.
Понятие производной. Вычисление производных.
Исходя из определения производной, найдите производную функции:

Вычислить производные:





2.17. Найти значение производной функции  :
:
 Найти
Найти 
 Найти
Найти 
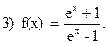 Найти
Найти 
 Найти
Найти 
Пользуясь правилом дифференцирования сложной функции, найти производные функций:

2.44. y=cos (x2 +2x - 4). 2.45. y=sin (x3 - 3x +5).
2.46. y=sin ex. 2.47. y=cos ln x.
2.48. y=e 2x-3. 2.49. y=e  .
.
2.50. y=etgx . 2.51. y=esinx.
2.52. y= ln(1+2  ). 2.53. y= ln(2x2 +4x -1).
). 2.53. y= ln(2x2 +4x -1).
2.54. y= ln cos x. 2.55. y=ln(2ex+3).
2.56. y= (3x+2)11. 2.57. y=(x3+x2+1)10.
2.58. y= ln5 x. 2.59. y=(ex - 1)6.
2.60. y= sin2x. 2.61. y=cos3 x.
2.62. y= tg 10x. 2.63. y=ctg2 x.
2.64. y= ln (5x+7). 2.65. у= e2x-9.
2.66. y= sin 3x. 2.67. y=cos 10x.
2.68. y= tg  . 2.69. y=arctg 5x.
. 2.69. y=arctg 5x.
2.70. y= tg x2. 2.71. y= ctg ex.
2.72. y= arctg  . 2.73. y=arctg sinx.
. 2.73. y=arctg sinx.
2.74. y= arcsin ex. 2.75. y= arcsin  .
.
2.76. y=  . 2.77. y=
. 2.77. y=  .
.
2.78. y=  . 2.79. y=
. 2.79. y=  .
.
2.80. y= 2sin 3x +3cos 2x. 2.81. y= 2arctg 5x + e10x.
2.82. y= x ln (3x+1). 2.83. y=sinx ecos x.
2.84. y=  . 2.85. y=
. 2.85. y= 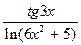 .
.
2.86. y= ln sin ex. 2.87. y= sin ln(ex+1).
2.88. y= cos3 x2. 2.89. y= sin2 x3.
2.90. y= e  . 2.91. y= arctg
. 2.91. y= arctg  .
.
2.92. y= 2arctg lnx. 2.93. y=  .
.
2.94. y= arcsin  . 2.95. y= arcsin e4x.
. 2.95. y= arcsin e4x.
2.96. y=  . 2.97. y=
. 2.97. y=  .
.
2.98. y= ln ( ). 2.99. y= ln ln(
). 2.99. y= ln ln( +10).
+10).
2.100. y= tg3  . 2.101. y= ctg5
. 2.101. y= ctg5  .
.
2.102. y= ln 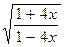 . 2.103. y= ln
. 2.103. y= ln  .
.
2.104. y=  . 2.105. y=
. 2.105. y=  .
.
2.106. y= ln cos  . 2.107. y=
. 2.107. y= 
2.108. y= e  . 2.109. y=
. 2.109. y=  .
.
2.110. y= tg sin cos 2x. 2.111. y= arccos  .
.
2.112. y= xsinx. 2.113. y=  .
.
Составить уравнения касательных к графикам функций:
2.114. y=x2 - 3x + 2 в точке (3;2).
2.115. y=  в точке (4;2).
в точке (4;2).
2.116. y= ln x в точке пересечения с осью Оx.
2.117. y= x2 - 5x + 6 в точках пересечения с осью Оx.
2.118. y=e7x в точке пересечения с осью Оy.
2.119. y=x3 - x2 + x + 1 в точке (-1;-2).
2.120. При каких значениях х касательные к графику функции
y=x3 -7x параллельны прямой y=5x?
2.121. Найти угол наклона к оси Оx касательной к гиперболе y=  в точке (1;1).
в точке (1;1).
Понятие дифференциала.
Производные и дифференциалы высших порядков.
Найти дифференциалы функций:
2.122. y= x3 - 3ln x. 2.123. y= cos x  ex.
ex.
2.124. y= sin 3x. 2.125. y= tg ln x.
2.126. y= x2 arctg x. 2.127. y=  .
.
2.128. y=  . 2.129. y=
. 2.129. y=  .
.
2.130. y= arcsin ex. 2.131. y=  .
.
2.132. y=  2.133. y=
2.133. y= 
2.134. Найти приращение  y и дифференциал dy
y и дифференциал dy
1) функции у=х2, если х=3,  х=0,01;
х=0,01;
2) функции у=  , если х=1,
, если х=1,  х= -0,2;
х= -0,2;
3) функции у=  , если х= 1,
, если х= 1,  х=-0,1351;
х=-0,1351;
4) функции у= x3, если х= 1,  х= 0,1.
х= 0,1.
2.135. Найти приближенно приращение  у:
у:
1) функции у=  , если х= 4,
, если х= 4,  х= 0,08;
х= 0,08;
2) функции у= sinx, если х=  ,
,  х= 0,02;
х= 0,02;
3) функции у= lnx, если х= 5,  х= -0,1.
х= -0,1.
Найти производные 2-го порядка от функций:
2.136. у= sin2x. 2.137. у= arctg x.
2.138. у= x2 lnx. 2.139. у= ex  sin x.
sin x.
2.140. у= arcsin x. 2.141. у= ln cosx.
2.142. у= e 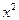 . 2.143. у=
. 2.143. у=  .
.
2.144. у= ctg x. 2.145. у=  .
.
Найти производные 3-го порядка от функций:
2.146. y=ex  cosx. 2.147. y= x2
cosx. 2.147. y= x2  ex.
ex.
2.148. y=ln(2x+5). 2.149. y= xlnx.
Найти производные n-го порядка от функций:
2.150. y=  . 2.151. y= e2x.
. 2.151. y= e2x.
2.152. y= 5x. 2.153. y= ln(1+x).
2.154. y= xex. 2.155. y= (2x-3)n.
Найти дифференциалы 2-го порядка от функций:
2.156. y= x3 - 3x2 + x + 1. 2.157. y= (0,1x+1)5.
2.158. y= xcos2x. 2.159. y= sin2x.
2.160. y= 25  x2. 2.161. y= ln(1+x2).
x2. 2.161. y= ln(1+x2).
2.3.Основные теоремы дифференциального исчисления.
Правило Лопиталя.
2.162. Удовлетворяют ли условиям теоремы Ролля функции:
1) f(x)=x, x  [0,1];
[0,1];
2) f(x)=  ;
;
3) f(x)=  , x
, x  [-1,1]?
[-1,1]?
Пояснить графически.
2.163. Применима ли теорема Ролля к функции f(x)=1 -  на
на
отрезке [-1,1]?
2.164. Удовлетворяют ли условиям теоремы Ролля функции:
1) f(x) = sinx на отрезке [  ];
];
2) f(x) =  на отрезке [ -2,2];
на отрезке [ -2,2];
3) f(x) = x2 -2x-15 на отрезке [ 0,2];
4) f(x) = x3 +2x2 -x -2 на отрезке [ -1,1];
5) f(x) =  на отрезке [
на отрезке [  ];
];
6) f(x) =  на отрезке [
на отрезке [  ]?
]?
В случае применимости теоремы найти точку с, в которой  .
.
2.165. Доказать, что уравнение х3 +3х - 5 = 0 имеет только один вещественный корень.
2.166. Проверить, применима ли теорема Лагранжа к функциям:
1) f(x) = x3 на отрезке [-1,1];
2) f(x) =  на отрезке [ 0,4];
на отрезке [ 0,4];
3) f(x) = ln x на отрезке [1,2];
4) f(x) = x2 - 3x + 2 на отрезке [ 3,5];
5) f(x) =  на отрезке [-1,2].
на отрезке [-1,2].
В случае применимости найти точку с, для которой 
где а,b - концы указанных отрезков.
2.167. Написать формулу Лагранжа для функции f(x)=x2 на отрезке [a,b] и найти с. Пояснить графически.
2.168. В какой точке касательная к параболе у=х2 параллельна хорде, стягивающей точки А(-1;1) и В(3;9)? Пояснить графически.
2.169. В какой точке касательная к кривой у=arctg x параллельна хорде, стягивающей точки А(0;0) и В(1;  ?
?
2.170. Построить график функции у=  на отрезке [0,3]. Почему здесь нельзя провести касательную, параллельную хорде? Какое из условий теоремы Лагранжа здесь не выполнено?
на отрезке [0,3]. Почему здесь нельзя провести касательную, параллельную хорде? Какое из условий теоремы Лагранжа здесь не выполнено?
2.171. Проверить, что функции:
1) f(x) =sin x и g(x)=cosx на отрезке 
2) f(x) = x2 и g(x)=  на отрезке [ 1,4];
на отрезке [ 1,4];
3) f(x) = x2 +2x + 3 и g(x) =x3 +1 на отрезке [ 0,1];
4) f(x) = x3 и g(x)=x2 на отрезке [a,b], 0  [a,b],
[a,b],
удовлетворяют условиям теоремы Коши. Для каждой пары функций
найти точку с, в которой  где а,b - концы указанных отрезков.
где а,b - концы указанных отрезков.
2.172. Удовлетворяют ли условиям теоремы Коши функции f(x)=ex
и g(x)= 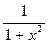 на отрезке [-2,2]?
на отрезке [-2,2]?
Найти пределы с помощью правила Лопиталя:
2.173.  2.174.
2.174. 
2.175.  2.176.
2.176. 
2.177.  2.178.
2.178. 
2.179.  2.180.
2.180. 
2.181.  2.182.
2.182. 
2.183.  2.184.
2.184. 
2.185.  2.186.
2.186. 
2.187.  2.188.
2.188. 
2.189.  2.190.
2.190. 
2.191.  2.192.
2.192. 
2.193.  2.194.
2.194. 
2.195.  2.196.
2.196. 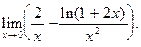
2.197.  2.198.
2.198. 
2.199.  2.200.
2.200. 
2.201. 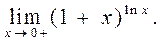
2.202. 
2.4. Исследование функций и построение графиков.
2.203. Найти максимумы и минимумы и промежутки возрастания и убывания функций:
1) f(x)=x3 - 3x2 - 9x + 5; 2) f(x)= 
3) f(x)=xlnx; 4) f(x)= x - arctg2x;
5) f(x)=x2e-x.
2.204. Найти интервалы выпуклости и точки перегиба графика функций:
1) f(x)=x3- 12x2  +5x - 1; 2) f(x)=
+5x - 1; 2) f(x)= 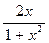 ;
;
3) f(x)=x2lnx; 4) f(x)=x arctgx.
Исследовать функции и построить их графики:
2.205. у=e  . 2.206. у=12х-х3.
. 2.206. у=12х-х3.
2.207. у=  2.208. у=
2.208. у= 
2.209. у= 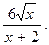 2.210. у=
2.210. у= 
2.211. у= x ln2 x. 2.212. у= x - lnx.
2.213. у=  2.214. у=
2.214. у= 
2.215. у= x+ arctgx. 2.216. у= x- arctg 2x.
2.217. y=  2.218. y=x2
2.218. y=x2  .
.
2.219. В промышленности нужно разместить заказ на изготовление цилиндрической емкости для расфасовки жидкого продукта. Каковы должны быть радиус основания и высота емкости, чтобы при заданном объеме V затраты на материал для ее изготовления были минимальными? Учесть при этом, что затраты на материал пропорциональны площади поверхности емкости.
2.220. Объем пакета в форме параллелепипеда для расфасовки молока равен W. Каковы должны быть стороны основания, чтобы затраты на материал упаковки были минимальными, если стороны основания относятся как 1:2. Принять, что затраты на материал пропорциональны площади поверхности пакета.
2.221. Переносной торговый павильон имеет форму конуса, для которого необходимо заказать ткань для покрытия. Каково должно быть соотношение между высотой и радиусом конуса, чтобы при заданной вместимости (объема) павильона W было затрачено минимальное количество материи?
2.222. Прямоугольная площадка, примыкающая одной стороной к каменной стене, с трех сторон огорожена железной решеткой. Какова должна быть длина сторон площадки, чтобы она имела наибольшую площадь, если имеется 200 м решетки?
2.223. Бак без крышки с квадратным основанием должен иметь объем 1 м3. Каково должно быть отношение стороны основания бака к высоте, чтобы на его изготовление пошло наименьшее количество материала?
2.224. Кооператив имеет грузовой автомобиль. Расходы на топливо для автомобиля пропорциональны кубу средней скорости его движения. Известно, что при скорости 20 км/час расходы на топливо составляют 4 у.е. в час; остальные же расходы, не зависящие от скорости, составляют 625 у.е. в час. При какой скорости движения автомобиля общая сумма расходов на 1 км пути будет наименьшая?
2.225. Директору универмага нужно принять решение о том, какого вида рекламное объявление целесообразно разместить в местной газете. Объем рекламного объявления (число строк) определяет объем продажи товара в стоимостном выражении, но не так однозначно, как этого бы хотелось: излишнее многословие в рекламе портит дело, и, если при объявлении в 20 строк текста ожидаемый объем продаж товара достигает 5800 у.е., то при объявлении в 60 строк текста объем продаж снижается до 2200 у.е. Связь между размером объявления и объемом продаж описывается зависимостью az2+bz+4000, где z - число строк в объявлении.Определить количество строк в рекламе, обеспечивающих универмагу максимальную выручку (с учетом расходов на рекламу), и размер этой выручки. Стоимость строки в объявлении составляет 30 у.е..
2.226. Директор продовольственного магазина установил из повседневной практики, что прибыль С(х) возрастает при увеличении объема завозимых продуктов х (кг) до определенного значения, а затем убывает при больших значениях х, так как слишком большой запас продуктов приводит к возникновению значительных затрат, связанных с их хранением и транспортировкой внутри магазина. Определите, какое количество продуктов (кг) следует завезти единовременно в магазин, чтобы прибыль от их продажи достигала максимального значения. Известно, что при завозе 300 кг продуктов прибыль составляет 10600 у.е., а при завозе 2,5 тонн продуктов прибыль увеличивается до 15000 у.е. Принять при этом С(х) =ах2+bх.
2.227. Зависимость финансовых накоплений предприятия от объема выпуска продукции имеет вид:
А=-0,01 х3 +300х - 500.
Определить, при каком объеме выпуска продукции финансовые накопления предприятия убывают и при каком возрастают.
2.228. На предприятии переменные издержки К в зависимости от объема выпуска продукции V составляют:
К=  V3 -
V3 -  V2 + 80V +300.
V2 + 80V +300.
Исследовать, как изменяются издержки при изменении объема выпуска продукции. Построить график К (V).
2.229. В какой точке кривой у=х3, х  [1,2] следует провести касательную, чтобы она пересекала прямые х=1 и х=2 в точках, сумма расстояний до которых от оси абсцисс наибольшая. Написать уравнение этой касательной.
[1,2] следует провести касательную, чтобы она пересекала прямые х=1 и х=2 в точках, сумма расстояний до которых от оси абсцисс наибольшая. Написать уравнение этой касательной.
2.230. При каких а<0 касательная к графику функции у= 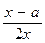 в точке с абсциссой х=0,5 отсекает от координатного угла треугольник с наименьшей суммой длин катетов?
в точке с абсциссой х=0,5 отсекает от координатного угла треугольник с наименьшей суммой длин катетов?
2.5. Применение дифференциального исчисления в экономических вопросах.
2.231. Зависимость спроса (объема продаж) от цены выражается формулой d(p)=  . Определить, для каких p спрос эластичен, неэластичен, нейтрален.
. Определить, для каких p спрос эластичен, неэластичен, нейтрален.
2.232. Зависимость спроса от цены при р  выражается формулой d(p)=
выражается формулой d(p)=  , где
, где 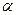 >0-const. Определить, когда спрос будет эластичен, неэластичен, нейтрален.
>0-const. Определить, когда спрос будет эластичен, неэластичен, нейтрален.
2.233. Пусть х - объем продаж некоторого товара торговой фирмой, р(х) - функция спроса (выражает зависимость между ценой и объемом продаж), Z(х)- функция издержек (затраты фирмы на реализацию товара). Учитывая, что прибыль от продажи товара находится по формуле V(x) = x p(x) - Z(x), определить:
а) интервалы значений объемов продаж, при которых торговля этим товаром будет прибыльной (убыточной);
б) оптимальные значения объема продаж х* и цены р*, обеспечивающие максимум прибыли V(x), вычислить Vmax.
Используя эскизы графиков функций выручки W(x) =x p(x) и функции издержек Z(x), дать геометрическую интерпретацию полученным результатам.
Выполнить задание для случаев:
1) р(х)=155-3х, Z(x)=1800+5х;
2) р(х)= 100-2х, Z(x)= 375+3х2;
3) р(х)=  Z(x)=21+х;
Z(x)=21+х;
4) р(х)=  Z(x)=20+0,5x.
Z(x)=20+0,5x. 
В задачах 2.234 - 2.238 х-объем продаж некоторого товара торговой фирмой, Z(x) - функция издержек (затраты фирмы на реализацию товара), р0 - равновесная рыночная цена товара, W(x)=p0 x - выручка фирмы, V(x)= p0 x - Z(x) - прибыль фирмы от продажи рассматриваемого товара.
2.234. Определить:
а) интервалы значений объемов продаж, при которых торговля этим товаром будет прибыльной (убыточной);
б) оптимальный объем продаж х*, обеспечивающий максимум прибыли V(x), вычислить max V(x).
Выполнить задание для случаев:
1) р0 =165, Z(x)= 3200 +5х;
2) р0 =650, Z(x)= 9000 +10х2;
3) р0 =560, Z(x)= 9600 +8х2.
Используя эскизы графиков функций W(x) и Z(x), дать геометрическую интерпретацию полученным результатам.
2.235. При каких значениях рыночной цены р0 фирма будет иметь прибыль хотя бы при некоторых объемах продаж, если:
1) Z(x)= 3200+5х; 2) Z(x)=1000+10х;
3) Z(x)= 9000+10х2; 4) Z(x)= 9800 +8х2 ?
Дать геометрическую интерпретацию полученным результатам.
2.236. При каких значениях рыночной цены р0 фирма будет иметь убытки при любых объемах продаж, если:
1) Z(x)= 1800+5х;
2) 2) Z(x)=5000+4х2 ?
2.237. При каких значениях параметра b0  фирма будет иметь прибыль хотя бы при некоторых объемах продаж, если:
фирма будет иметь прибыль хотя бы при некоторых объемах продаж, если:
1) р0 =165, Z(x)= b0 +5х;
2) р0 =640, Z(x)= b0 +10х2;
3) р0 =560, Z(x)= b0 +8х2?
2.238. При каких значениях параметра b1  фирма будет иметь убытки при любых объемах продаж, если:
фирма будет иметь убытки при любых объемах продаж, если:
1) р0 =165, Z(x)= 3200+b1х;
2) р0 =50, Z(x)= 1000+b1х;
3) р0 =750, Z(x)= 9000 +b1х2;
4) р0 =560, Z(x)= 9600 +b1х2?
Тема 3. Дифференциальное исчисление функций нескольких переменных.






