Исследование затухающих колебаний
в колебательном контуре
Цель работы: изучить затухающие колебания в электрическом колебательном контуре. Определить период свободных затухающих колебаний, логарифмический декремент затухания и исследовать зависимость периода свободных колебаний от параметров контура.
Приборы и оборудование: осциллограф, лабораторный макет установки для возбуждения колебаний, конденсатор, две эталонных катушки индуктивности, переменное сопротивление, соединительные провода, дроссельная катушка 1200 витков.
КРАТКАЯ ТЕОРИЯ
Электрическими колебаниями называют периодические изменения тока и напряжения в электрической цепи. В общем случае в каждый момент времени при колебаниях ток на разных участках цепи оказывается не одинаковым, так как электромагнитные возмущения распространяются с конечной скоростью, хотя и с очень большой. Однако во многих случаях изменения тока происходят достаточно медленно и можно считать его одинаковым во всех участках цепи. Такой ток называют квазистационарным. Для расчётов квазистационарных токов можно пользоваться формулами для статических полей. В частности, можно применять закон Ома для мгновенных значений тока и напряжения.
Изучать электромагнитные колебания удобнее всего с помощью колебательного контура, состоящего из электрической ёмкости С и индуктивности L.
Свободные колебания происходят в изолированном контуре после подействовавшего на него внешнего возмущения. Понятие свободные колебания означает, что процесс колебаний в этом случае определяется (в основном) свойствами контура.
Для возбуждения колебаний в состав колебательного контура необходимо включить источник ЭДС Е и ключи К 1 и К 2, как показано на рис. 1.
Рис.1. Схема возбуждения колебаний в колебательном контуре.
|
В начальный момент ключ К 1 разомкнут, а ключ К 2 замкнут. После зарядки конденсатора до напряжения U 0 ключ К 2 размыкается, а ключ К 1 замыкается, и в колебательном контуре возникают электромагнитные колебания.
Начальные условия, при которых возникают свободные колебания, определяют начальную фазу процесса и амплитуду колебаний. Характер же процесса свободных колебаний, как следует из данного выше определения этого типа колебаний, зависит от свойств самой системы.
Напомним вкратце ход процесса электромагнитных колебаний в контуре, имеющий место при любых начальных условиях. Процесс колебаний в таком контуре заключается в периодической перезарядке конденсатора и протекании переменного тока в цепи, замыкающей пластины конденсатора. При этих колебаниях энергия электростатического поля заряженного конденсатора C периодически переходит в энергию магнитного поля, запасаемую в индуктивности L. В результате наличия в контуре неизбежного активного сопротивления R (сопротивления потерь энергии) первоначальный запас энергии системы расходуется (даже при отсутствии резистора) на выделение тепла в проводах, составляющих контур и индуктивность L. Поэтому разряд конденсатора через такой контур является процессом не вполне периодическим. Амплитуда напряжения на конденсаторе после каждой его перезарядки становится все меньше; амплитуда тока также убывает со временем.
Сила тока в контуре связана с зарядом и разностью потенциалов на конденсаторе соотношением:
,
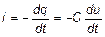где q = Cu - есть заряд конденсатора. Знак «минус» указывает на то, что положительным считается то направление тока, которое соответствует убыли разности потенциалов на пластинах конденсатора. Изменение силы этого тока в катушке индуктивности вызывает электродвижущую силу самоиндукции, равную
.
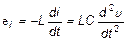Согласно второму закону Кирхгофа u + e i = iR. Подставляя значения e i и i, получим:
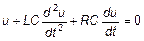
или
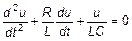(1)
Введём новые обозначения:
; 
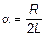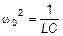, (2)
где a - коэффициент затухания; w0 – циклическая частота собственных колебаний (колебаний без затухания), и перепишем формулу (1) в виде:
. (3)
Уравнения (1) и (3) есть уравнения свободных колебаний в контуре, составленном из L, С и R. Если выполняется условие a < w0, то решение уравнения (3) может быть записано в форме:
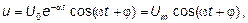(4)
где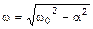 
есть циклическая частота свободных колебаний в контуре, U0 и j - константы, зависящие от начальных условий колебательного процесса, а Um – амплитуда.
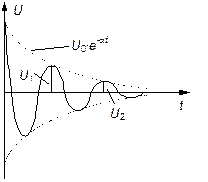Рис.2. Вид затухающих колебаний.
|
Из решения следует, что напряжение на конденсаторе U с течением времени изменяется по гармоническому закону с амплитудой колебаний, убывающей со временем по экспоненциальному закону:
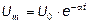, (5)
где U 0 - начальное напряжение на конденсаторе (при t = 0). Вид затухающих колебаний представлен на рис.2.
Период свободных колебаний выражается формулой
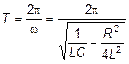(6)
Если a << w0, то членом R 2/4 L 2 можно пренебречь, и мы получим формулу Томсона:
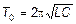, (7)
определяющую период свободных колебаний в контуре без затухания.
Величина a, определяющая степень затухания, называется коэффициентом затухания. На практике вместо нее часто употребляется другая мера затухания:
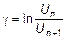(8)
где Un и Un +1 - величины последовательных амплитуд, отстоящих друг от друга на один период. Величина g называется логарифмическим декрементом затухания. Ёе связь с a можно установить следующим образом. Так как Un +1 = Un Ч e- a t, то Un / Un+ 1 = e a t. Отсюда следует:
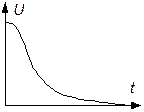Рис. 3. Апериодический режим колебаний.
|
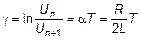. (9)
Из уравнения (9) видно, что чем меньше R и чем больше L, тем меньше затухание, тем ближе подходит описываемая выражением (4) кривая к гармонической функции, и тем ближе период Т к величине Т 0, определенной по формуле Томсона. Наоборот, при значительном возрастании R затухание, так же как и период, увеличивается. При a > w0, когда вещественного решения уравнения (3) не существует, разряд будет изображаться кривой, приведенной на рис.3; такой процесс называется апериодическим. Режим, который разграничивает колебательный и апериодический процессы (a = w0), называется критическим, а соответствующее сопротивление потерь в контуре определяется формулой:
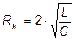(10)
ПРАКТИЧЕСКАЯ ЧАСТЬ
Описание установки. Схема установки для наблюдения осциллограммы свободных колебаний показана на рис. 4.
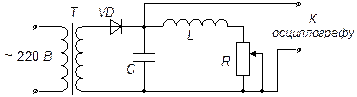
Рис. 4. Схема установки для наблюдения затухающих колебаний.
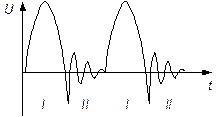Рис. 5. Примерная осциллограмма напряжения на конденсаторе.
|
Конденсатор С, катушка индуктивности L и переменное сопротивление R образуют колебательный контур с потерями. Колебания в контуре (колебания напряжения на конденсаторе) наблюдаются с помощью осциллографа. Примерный вид осциллограммы показан на рис. 5. Диод VD предназначен для периодического возбуждения в контуре свободных колебаний. Рассмотрим упрощенно работу этой установки. В течение положительного полупериода питающего напряжения диод открыт (его сопротивление близко к нулю) и в контур поступает энергия; контур работает в режиме вынужденных колебаний, что соответствует участку I на рис. 5. При отрицательном полупериоде питающего напряжения диод заперт (его сопротивление очень велико) и в контуре наблюдается режим свободных затухающих колебаний (участок II на рис. 5).
Упражнение 1. Определение периода свободных колебаний
1. Собрать колебательный контур, взяв для этого эталонную катушку с индуктивностью L = 0,001 Гн, конденсатор емкостью С = 1,0 мкФ и потенциометр R = 30…50 Ом, чтобы наблюдать на экране осциллографа не менее 6…8 периодов свободных колебаний.
2. Подготовить к работе установку по схеме, представленной на рис.4. Конденсатор контура соединить со входом «Y» осциллографа. Подвижный контакт потенциометра поставить в верхнее положение (R = 0).
3. Включить осциллограф и на его экране добиться четкой картины затухающих колебаний, регулируя режим синхронизации, скорость развёртки и чувствительность канала. Пользуясь регулятором усиления и рукояткой смещения луча по горизонтали, установить на экране осциллографа рабочий участок осциллограммы, соответствующий свободным колебаниям.
4. Измерить частоту и период свободных колебаний.
