Из формулы (11) следует, что
,
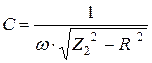где Z 2 и R – соответственно полное и активное сопротивление цепи.
В случае, когда напряжение Uэфф измеряется непосредственно на обкладках конденсатора, можно считать, что активное сопротивление в цепи отсутствует (R = 0), поэтому:
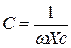. (15)
Рис.2.
|
Для определения Z 2 поступают следующим образом: соединяют последовательно измеряемый конденсатор C, амперметр А и реостат r и подключают их к средним клеммам ключа К (рис.2). Параллельно конденсатору присоединяют вольтметр. Реостат служит здесь лишь предохранителем на случай пробоя или короткого замыкания обкладок конденсатора и должен быть включен на максимальное сопротивление.
Порядок выполнения.
Замыкают ключ на переменный ток и отсчитывают по прибору силу тока Iэфф и напряжение Uэфф. Определив Z 2 по формуле
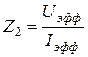
подставляют это значение Z 2 в формулу (15) и вычисляют С. Измерения производят сначала отдельно для каждого из двух конденсаторов, а затем при параллельном и последовательном их соединении, проверяя тем самым формулы соединений конденсаторов.
Упражнение 3. Проверка полного закона Ома для переменного тока.
Из формулы (11) для случая последовательно включенных сопротивления, индуктивности и ёмкости имеем:
, (16)
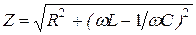. (17)
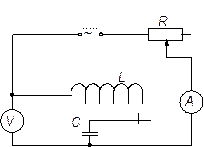Рис.3.
|
Для проверки этой формулы в цепь переменного тока включают последовательно: катушку индуктивности с известным активным сопротивлением R и индуктивностью L, конденсатор с известной емкостью С, реостат r и амперметр А (рис.3). Параллельно части цепи, содержащей катушку и конденсатор, подключают вольтметр V.
Порядок выполнения.
Установив реостат на максимум сопротивления, замыкают ключ К на переменный ток. Изменяя затем сопротивление реостата, добиваются достаточных показаний приборов и производят отсчет Iэфф и Uэфф. Полученные результаты подставляют в правую часть формулы (16) и вычисляют R. С другой стороны, значение R определяется из формулы (17) по известным величинам R, L, С.
Полученные результаты сравнивают для проверки справедливости формулы полного закона Ома для переменного тока. Отчет по задаче представляют в виде таблицы измеренных и вычисленных величин сопротивлений участков цепи для переменного тока.
КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Вывести выражение для величин индуктивного и емкостного сопротивления.
2. Начертить векторную диаграмму напряжений для последовательного соединения сопротивления, емкости и индуктивности.
3. Сформулировать закон Ома для переменного тока.
4. Чему равна разность фаз между током и полным напряжением в цепи (рис.3)? Чему равна разность фаз между напряжением на емкости и индуктивности?
Рекомендуемая ЛИТЕРАТУРА.
1. Калашников С.Г. Электричество. - М.: Наука, 1970.
2. Фриш С.Э., Тимофеева А.В. Курс общей физики. Т.2.-М.: Физматгиз, 1962.
3. Руководство к лабораторным занятиям по физике. Под ред. Л.Л.Гольдина. - М.: Наука, 1973.
4. Практикум по общей физике. Под ред. проф. В.Ф.Ноздрева. - М.: Просвещение, 1971.
5. Савельев И.В. Курс физики, т.II, Электричество. - М.: Наука, 1973.
6. Матвеев А.Н. Электричество и магнетизм. – М.: Высшая школа, 1983.
7. Сивухин Д.В. Общий курс физики. Электричество. – М.: Наука, 1983.
физический практикум
«электричество и магнетизм» часть 1
Учебно-методические рекомендации
для студентов физического факультета
Михеев Владимир Александрович
Монтанари Сергей Георгиевич
Дубов Владимир Петрович
Печать офсетная
Подписано в печать _________________ Заказ №_____________
Объем __________ п.л. Тираж _________________ экз.
Издательство Тюменского государственного университета
625003, г. Тюмень, ул. Семакова, 10
лаборатория
«электричество и магнетизм»
