При помощи электролитической ванны можно исследовать поля, обладающие осевой симметрией, т.е. поля, не зависящие от угловой координаты a в цилиндрической системе координат (r, a, Z).
Рис.2.
|
Ёмкость цилиндрического конденсатора, пропорциональная длине конденсатора, диэлектрической проницаемости среды, заполняющей конденсатор, а также зависит от отношения радиусов цилиндров, возрастая с уменьшением этого отношения (рис.2):
.
Из формулы ёмкости цилиндрического конденсатора можно получить выражение для разности потенциалов между его обкладками:
, (7)
где q = Q / L - заряд, приходящийся на единицу длины цилиндра.
Проверка формулы (7) составляет содержание данного упражнения.
Порядок выполнения.
Расположите два коаксиальных цилиндрических электрода как показано на рис. 3.
Рис.3.
|
Определите форму эквипотенциальных поверхностей и исследуйте распределение потенциалов вдоль радиуса цилиндра. Сравните найденное распределение потенциалов с теоретической формулой (7).
Сравнение проведите с помощью графиков. Сначала на основе результатов измерений постройте график экспериментальной зависимости Ux = f (Rx), откладывая по оси абсцисс значения Rx расстояние от оси цилиндра до той точки поля, где определялся потенциал.
Затем в этих же осях координат постройте теоретический график функции
.
Для того чтобы не определять величину 2 q /e, масштаб по оси ординат для теоретического графика следует выбрать таким, чтобы для какого-либо одного значения Rx масштабные отрезки в относительных единицах разности потенциалов и в вольтах были одинаковыми.
Если формула (7) справедлива, то теоретический и опытный графики функции должны совпасть.
КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Какова связь между напряженностью электростатического поля и потенциалом? Как экспериментально эта связь может быть проверена?
2. Чему равна циркуляция напряженности по любому замкнутому контуру в потенциальном электрическом поле? Как обосновать справедливость соответствующего уравнения?
3. Сформулируйте закон Кулона и теорему Гаусса.
4. Обоснуйте возможность моделирования электростатического поле в вакууме с помощью слабопроводящей жидкости?
5. Выполняются ли граничные условия на электродах ванны?
6. Почему необходимо, чтобы электроды касались дна ванны и выступали над поверхностью жидкости?
7. Чему равна напряженность электрического поля, создаваемого равномерно заряженной бесконечной цилиндрической поверхностью?
8. Вывести формулу емкости цилиндрического конденсатора.
Лабораторная работа №3
Изучение вынужденных колебаний и явления резонанса в последовательном колебательном контуре
Цель работы: построение резонансных кривых для колебательного контура, определение добротности и её зависимости от параметров контура.
Оборудование: исследуемый контур, набор резисторов, вольтметр переменного тока или осциллограф в качестве измерителя напряжения, генератор сигналов, соединительные проводники и кабели.
КРАТКАЯ ТЕОРИЯ
Рис.1. Последовательный колебательный контур.
|
В работе исследуются вынужденные колебания в колебательном контуре, соединенном с источником электродвижущей силы переменной частоты. В зависимости от того, как источник соединен с колебательным контуром, различают последовательные и параллельные колебательные контуры. В данной работе исследуется последовательный колебательный контур (рис.1).
При исследовании вынужденных колебаний большой интерес представляет изучение зависимости интенсивности колебаний от соотношения между частотой внешнего воздействия и собственной частотой незатухающих колебаний в системе.
Вынужденные электромагнитные колебания в контуре могут быть количественно охарактеризованы разными величинами: силой тока; напряжением на конденсаторе; напряжением на катушке индуктивности контура и т.д. Амплитуда каждой из этих величин выражается особой функцией частоты, имеющей характерный максимум при определённом значении частоты w р, называемой резонансной частотой. График такой функции называется резонансной кривой (рис.2).
Рис.2. Резонансная кривая (А – относительная амплитуда).
Уравнение для резонансной кривой может быть получено следующим образом.
Запишем, на основании второго закона Кирхгофа, уравнение вынужденных колебаний в последовательном колебательном контуре:
, (1)
или
. (2)
где E0 - амплитуда э.д.с. генератора, включенного в контур. Учитывая, что сила тока
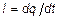, (3)
где q - заряд на конденсаторе, уравнение (2) можно записать в виде:
. (4)
Поделив обе части уравнения (4) на L, можно привести его к стандартному виду уравнения вынужденных колебаний гармонического осциллятора:
,
где 
– коэффициент затухания, характеризующий потери энергии; 
– квадрат собственной частоты колебательного контура.
Решение этого линейного неоднородного дифференциального уравнения второго порядка в режиме установившихся вынужденных колебаний будет иметь вид
, (5)
где q 0 – амплитуда заряда конденсатора, y – разность фаз между колебаниями заряда и внешней э.д.с. E.
Удобнее перейти от выражения для заряда (5) к выражению для тока I, воспользовавшись соотношением (3):
, (6)
где I 0 - амплитуда тока, j - сдвиг по фазе между током и внешней э.д.с. E:
, 
. (7)
С учётом этого, можно получить выражения для напряжений на сопротивлении R, ёмкости C и индуктивности L:
, (8)
, (9)
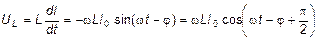, (10)
На основании выражений (8), (9) и (10) можно построить векторную диаграмму для амплитуд напряжений, векторная сумма которых должна быть равна, согласно (1), вектору величиной E0 (рис.2).
Рис.2. Векторная диаграмма для колебательного контура.
Из треугольника OAB этой диаграммы можно получить выражения для I 0 и j:
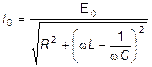, (11)
. (12)
Как видно из выражения (11), максимальное значение силы тока достигается при 
= 0. Таким образом, резонансная частота для силы тока равна собственной частоте колебательного контура:
(13)
Очевидно, что для напряжения на сопротивлении UR частота максимальной амплитуды колебаний w рR также совпадает с w0. Однако, для напряжений на ёмкости и на индуктивности это не так. Выражения для резонансных частот w рC и w рL можно получить, приравняв нулю первые производные по w для соответствующих выражений амплитуд U 0 C и U 0 L из (9) и (10):
, 
. (14)
Как видно, из формул (14), резонансная частота для напряжения на ёмкости меньше, а для напряжения на индуктивности – больше по сравнению с собственной частотой колебательного контура. Однако, чем меньше коэффициент затухания b (т.е., чем меньше потери энергии, обусловленные, в рамках модели, наличием активного сопротивления), тем ближе резонансные частоты w рC и w рL к значению w0. При 
все три резонансные частоты практически одинаковы.
Графики зависимости амплитуд напряжений U 0 R, U 0 C и U 0 L от частоты w показаны на рис.3.
Рис.3. Резонансные кривые колебательного контура со следующими параметрами: R = 1 Ом, C = 0,005 Ф, L = 0,02 Гн, E0 = 1 В.
Важным параметром колебательного контура, характеризующим его резонансные свойства, является добротность Q. Для колебательного контура с малым затуханием () добротность может быть определена как отношение энергии W, запасённой в контуре, к энергии d W, теряемой контуром за один период колебаний:
Величина добротности связана с коэффициентом затухания следующим образом:
(15).
Подставляя выражения для w0 и b, получим:
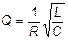. (16)
Выразим отношение амплитуды напряжения на конденсаторе U 0 C к амплитуде внешней э.д.с. E0 на резонансной частоте в случае малого затухания (w рC» w0), используя (9) и (11):
(17)
Таким образом, при резонансе в последовательном колебательном контуре амплитуда напряжения на конденсаторе в Q раз превышает амплитуду выходного напряжения генератора. Аналогичный результат можно получить и для амплитуды напряжения на индуктивности. Поэтому резонанс в последовательном колебательном контуре называют резонансом напряжений.
Добротность контура связана также с ещё одной важной характеристикой резонансной кривой – её шириной. Можно показать, что при малом затухании
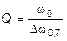, (18)
где Dw0,7 – ширина резонансной кривой на уровне 0,7 (точнее,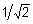 
) от максимума (см. рис. 2). Формула (18) даёт практический способ определения добротности колебательного контура по измеренной резонансной кривой.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Упражнение.
В данной работе исследуется зависимость амплитуды переменного напряжения на конденсаторе U 0 C от частоты f = w/2p при различных значениях активного сопротивления R.
Порядок выполнения.
Рис.4.
|
1. Соберите схему в соответствии с рис.4. В качестве вольтметра используйте осциллограф. Выходное напряжение генератора должно быть в пределах 2…4 В. При работе следует поддерживать постоянство заданной величины выходного напряжения генератора при изменении частоты, осуществляя контроль либо по встроенному измерительному прибору, либо используя имеющийся осциллограф.
2. Установите вместо сопротивления R перемычку. Изменяя частоту генератора в пределах 20 Гц…200 кГц, найдите частоту fр, на которой достигается максимальное значение амплитуды напряжения на конденсаторе. Затем снимите резонансную кривую, занося данные измерения зависимости амплитуды напряжения от частоты в таблицу. Измерения рекомендуется производить в диапазоне частот от fн до fв, где fн и fв – частоты, на которых амплитуда напряжения уменьшается примерно в 2…2,5 раза от максимальной.
3. Аналогичным образом снимите резонансные кривые для двух различных значений сопротивления R (1…10 Ом).
4. Полученные результаты измерений представьте в виде графиков резонансных кривых, строя зависимости U 0 С от f.
На основе каждого из построенных графиков необходимо:
1) определить резонансную частоту fр;
2) определить ширину резонансной кривой D f 0,7;
3) вычислить добротность по формуле (18);
4) найти величину коэффициента затухания по формуле (15).
Кроме того, для каждой резонансной кривой рассчитайте отношение 
и сравните полученные результаты с ранее рассчитанными значениями добротности.
КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Запишите и объясните вид уравнения вынужденных колебаний.
2. Нарисуйте векторную диаграмму для последовательного колебательного контура.
3. Выведите условие резонанса для последовательного колебательного контура.
4. Как зависят резонансные свойства колебательного контура от величины потерь, какова природа этих потерь?
5. Что такое добротность контура?
6. Как определить Q из резонансных кривых и какова её связь с коэффициентом затухания контура?
7. Почему U 0 L и U 0 C при резонансе могут быть больше E0? Почему при резонансе UL + UC = 0?
Лабораторная работа №4
проверка закона Ома для цепей переменного тока
Цель работы: Экспериментальное определение индуктивности, ёмкости и проверка закона Ома для цепей переменного тока.
Оборудование: катушка индуктивности и два конденсатора, реостат, источник постоянного и переменного напряжения, мультиметры в качестве вольтметра и амперметра, соединительные проводники.
КРАТКАЯ ТЕОРИЯ.
Если к концам проводника с активным сопротивлением приложена переменная электродвижущая сила, величина которой в каждый момент времени определяется уравнением
U = U m×cosw t, (1)
где U m - амплитуда, а w - круговая частота, то в нем возникает переменный электрический ток, сила которого в тот же момент времени определяется по закону Ома:
. (2)
Если же, помимо сопротивления R, в цепи имеется индуктивность, характеризуемая коэффициентом самоиндукции L, то под действием той же электродвижущей силы возникает ток силой
. (3)
где j- сдвиг фаз между током и напряжением, определяемый из формулы
. (4)
Из сопоставления уравнений (1) и (3) следует, что в этом случае ток отстает по фазе от напряжения.
Величина 
носит название полного сопротивления (импеданс), так как она играет в формуле (4) ту же роль, что и обычное активное сопротивление R в формуле закона Ома. Величина же w L называется индуктивным сопротивлением.
Если вместо индуктивности в цепь переменного тока включена ёмкость С, то сила тока выражается формулой
, (5)
а
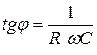. (6)
В этом случае сила тока опережает по фазе напряжение. Полное сопротивление цепи Z2 теперь запишется как 
, причем величина 1/(wС) называется ёмкостным сопротивлением.
Наконец, в случае, когда в цепь включены последовательно все три величины - R, L и С, сила тока в цепи может быть записана выражением
. (7 а)
(7 б)
При этом полное сопротивление равно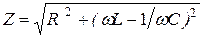 
.
Выражение (7) носит название формулы закона Ома для переменного тока.
В формулы (2), (3), (5) и (7) входят I m и U m – максимальные (амплитудные) значения токов и напряжений. Так как измеряемые приборами эффективные значения этих величин, Iэфф и Uэфф, связаны с максимальными посредством формул:
и 
,
то, подставляя отсюда I m и U m в вышеуказанные формулы, получим:
, (8)
(9)
(10)
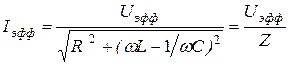(11)
Во всех этих формулах под R следует подразумевать сумму всех активных сопротивлений цепи (в том числе и катушки индуктивности), на концах которой измеряется электродвижущая сила. Если разность потенциалов измеряется непосредственно на зажимах катушки, то R есть активное сопротивление одной лишь катушки.
ПРАКТИЧЕСКАЯ ЧАСТЬ
