Пусть f(x) определена в окрестности т. х. Тогда. если $ 
то он называется производной функции f(x) и обозначается f ¢(x). Операция нахождения производной функции называется дифференцированием. Другие обозначения производной y¢, y¢x, 
.
Функцию, имеющую производную в каждой точке интервала (a, b) называют дифференируемой на интервале (a, b)
|
Если функция y=f(x) дифференцируема в т. х, то она непрерывна в этой точке. В точке разрыва функция не может иметь производную.
Брать производную по определению достаточно трудоемкое занятие, поэтому для облегчения придумана таблица производных и несколько правил.
| 
| 
| 
|
| 
| 
| 
|
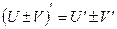
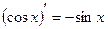
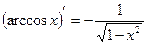
частный случай 
| 
| 
| 
|
частный случай 
| 
| 
| 
|
Последним столбцом в таблице представлены правила дифференцирования. Особую сложность, как правило, представляет последнее правило, означающее, что в случае дифференцирования сложной (не табличной функции) необходимо предпоследнее действие обозначить за новую переменную, взять производную от функции по этой новой переменной и помножить ее на производную от этой переменной.
Отдельно необходимо остановиться на взятии производных от функций:
Производная от показательно степенной функции 
.
Если функция заданна параметрически 
, тогда 
В случае если функция заданна неявно, то вычисляется производная от всего выражения, а затем выражается y¢ через переменную x и саму функцию y.
Производной n-го порядка называется производная от производной (n-1)-го порядка: y(n)=(f(n-1)(x))¢.
Для приближенного вычисления значения функции в точках, в которых точное значение получить затруднительно используется формула: f(x+Dx)»f(x)+f¢(x)Dx.
Исследования функции и построение эскиза ее графика можно производить при помощи производных.
Асимптотой графика y=f(x) называется такая прямая, что расстояние d от переменной точки М графика до этой прямой при удалении М в ¥ стремится к 0
Исследование функции с целью построения ее графика проводится по следующим пунктам:
Асимптоты делятся на вертикальные и наклонные.
Необходимым и достаточным условием существования вертикальной асимптоты x= a для функции y=f(x) является 
.
Наклонные асимптоты имеют уравнение y=kx+b, где 
Исследование функции с целью построения ее графика проводится по следующим пунктам:
1) находятся область определения функции,
2) проверяются симметрия графика, периодичность;
3) Определяются координаты критических точек (т.е. точек в которых функция не определена, первая или вторая производные равны нулю или не существуют).
4) Вся область определения делится критическими точками на интервалы монотонности и в каждом из этих интервалов определяются знаки первой и второй производной.
5) Используя свойства:
а) если при переходе т. х0 в направлении возрастания х f¢(x) меняет знак с (+) на (-), то в т.х0 функция имеет max, если с (-)на (+)-то min;
б) если f¢¢(x)<0 на (a,b), то график f(x) выпуклый вверх, если f¢¢ (x)>0 то график f(x) выпуклый вниз.
находятся интервалы монотонности, экстремумы, интервалы выпуклости, вогнутости и точки перегиба
6) находятся асимптоты графика функции;
7) проводится в случае необходимости исследование на концах области определения;
8) строится график функции.
В некоторых случаях приходится иметь дело с функциями двух, трех и более переменных.
Функцией n переменных y=f(x1,x2,...,xn), определенной на множестве DÌ Rn и принимающей значения на множестве YÌ R, называется такое соответствие между множествами D и Y, при котором для любой точки (x1,x2,...,xn)ÎD существует единственный элемент yÎY(D 
Y:" (x1,x2,...,xn) Î D Ì R n $! yÎY Ì R Û y=f(x1,x2,...,xn), (х1, х2,..., xn)Î D Ì R n, yÎYÌ R)
Для функций многих переменных определено понятие частной производной 
при вычислении производной по xi все остальные переменные считаются константами.
