Параметры k и b линейной модели у = kх + b из предыдущего раздела можно определить с помощью функций НАКЛОН и ОТРЕЗОК.
Функция НАКЛОН определяет угловой коэффициент линейного тренда, а функция ОТРЕЗОК –точку пересечения линии линейного тренда с осью ординат. Параметры этих функций – массивы значений y и x. На рис. 7.4. в ячейке D2 и Е2 были введены соответствующие функции: {=НАКЛОН (В2:В7;А2:А7)}, {=ОТРЕЗОК (В2:В7;А2:А7)}. Результаты вычисления этих коэффициентов совпадают с результатами предыдущего способа решения задачи.
Рис. 7.4. Нахождение k и b с помощью функций НАКЛОН и ОТРЕЗОК.
Коэффициенты k и b можно найти еще одним способом. Для этого необходимо построить точечный график по диапазону ячеек А2:В7 и выделить точки графика одинарным щелчком левой клавиши мыши. Далее при вызове правой кнопкой контекстного меню выбрать команду Линии тренда. (Рис. 7.5.)
Рис. 7. 5. Начало построения линии тренда.
В диалоговом окне Линия тренда на вкладке Тип в группе Построение линии тренда (аппроксимация и сглаживание) нужно выбрать параметр Линейная (рис. 7.6.а), а на вкладке Параметры установить флажки Показывать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации (R-Z) (т. е. вывести на диаграмму значение квадрата коэффициента корреляции) (рис. 7.6.б).
а) Вкладка Тип
| 
б) Вкладка Параметры
|
Рис. 7. 6. Вкладки диалогового окна Линия тренда.
По коэффициенту корреляции R можно судить о правомерности использования линейного уравнения регрессии. Если он лежит в диапазоне от 0,9 до 1, то данную зависимость можно использовать для предсказания результата. Чем ближе к единице коэффициент корреляции, тем более обоснованно это указывает на линейную зависимость между наблюдаемыми величинами. Если коэффициент корреляции близок к -1, то это говорит об обратной зависимости между наблюдаемыми величинами.
Результат выполнения команды Линии тренда приведен на рис. 7.7. Как видно из рисунка, квадрат коэффициента корреляции равен 0,9723, следовательно, линейная модель может быть использована для предсказания результатов.
Рис. 7.7. График линии тренда.
Однако значение у в точках, не являющихся узлами таблицы, можно вычислить и без предварительного определения коэффициентов линейной модели с помощью функции ПРЕДСКАЗ. В качестве параметров передается: адрес ячейки, для которой предсказывается значение, массивы значений y и x. Например, для задачи из раздела 7.2. найдем предсказанное количество продаж на 7 неделе. Для этого выделим ячейку В8, предназначенную для записи предсказанного количества проданных автомобилей на 7 неделе, с помощью Мастера функций вызовем Статистическую функцию ПРЕДСКАЗ, заполним диалоговое окно как показано на рис. 7.8.а., нажмем ОК. И в ячейке В8 будет выведено предсказанное значение равное 18,6 (рис. 7.8.б.)
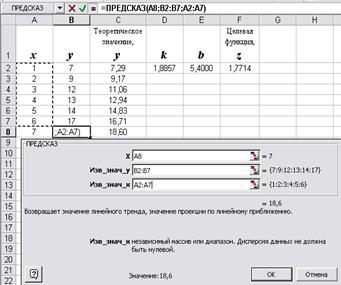а) Заполнение диалогового окна ПРЕДСКАЗ
| 
б) Результат
|
Рис. 7.8. Применение функции ПРЕДСКАЗ.
А теперь найдем это же значение уже известным нам способом, при помощи уравнения регрессии у = 1,88571 * х + 5,400. Для этого продолжим ряд х и в ячейку А8 введем число 7, зафиксируем его нажатием клавиши < ENTER >. В ячейке С9 по формуле =$D$2*A8+$E$2. автоматически просчиталось теоретическое значение у =18,60.(рис. 7.8)
Аналогом данной функции для многофакторной модели является функция тенденция.
Многофакторная линейная модель регрессии имеет вид у = k 1 х 1 +... + knхn + b. Массив коэффициентов { kn, kn-1,…, k 1, b } уравнения может быть определен с помощью функции ЛИНЕЙН.
Экспоненциальная модель
Другой часто встречающейся на практике регрессионной моделью является экспоненциальная модель, которая описывается уравнением у = b kx. Для определения коэффициентов зависимости используется функция ЛГРФПРИБЛ. Параметрами этой функции являются массивы значений у и x, логические параметры, указывающие на равенство 1 коэффициента b и необходимости вывода коэффициента корреляции.
Например, на рис. в диапазоне ячеек А2:В7 размещены значения x и у, а под значения искомых коэффициентов экспоненциальной модели b и k отведены ячейки F3, G3. Для заполнения ячеек коэффициентов необходимо:
v выделить ячейки F3, G3;
v вызвать Мастер функций и указать параметры функции или ввести { ЛГРФПРИБЛ(B2:B7;A2:A7) };
v при завершении ввода функции нажать < Ctrl + Shift + Enter > (для функций, возвращающих массивы).
Другим способом получения коэффициентов экспоненциальной модели и построения графической зависимости является использование линии тренда. На рис.7.9. изображен точечный график зависимости исследуемых величин и линия экспоненциального тренда.
Рис. 7.9. Экспоненциальная линия тренда.
Квадрат коэффициента корреляции (R2) экспоненциальной модели равен 0,947 (рис. 7.9.) и меньше квадрата коэффициента корреляции линейной модели (= 0,9923) (рис. 7.7.). Таким образом, в данном примере линейная модель более достоверно описывает зависимость между наблюдаемыми величинами.
