Общий подход к построению уравнения регрессии на примере линейной модели

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Понятие регрессии, регрессионной модели. Виды регрессионных моделей.

Термин регрессия применяется для описания любой статистической связи между случайными величинами.

Функция f(x₁, x₂, … x_m), описывающая зависимость показателя от параметров называется уравнением (функцией) регрессии. В регрессионных моделях зависимая (объясняемая) переменная у может быть представлена в виде функции регрессии f(x₁, x₂, … x_m), где x₁, x₂, … x_m – независимые (объясняющие) переменные или факторы.

В зависимости от вида функции f(x₁, x₂, … x_m) модели делятся линейные и нелинейные.

В зависимости от количества включенных в модель факторов x модели делятся на однофакторные (парная модель регрессии) и многофакторные.

Общий подход к построению уравнения регрессии на примере линейной модели.

Рассмотрим задачу построения линейного уравнения регрессии на примере фирмы, торгующей подержанными автомобилями. В фирме постоянно ведется журнал учета проданных автомобилей. В журнале ведутся две графы: количество проданных за неделю автомобилей и номер недели (Таблица 7.1.). Это наши две наблюдаемые величины. Фирма существует только 6 недель, поэтому данные по продажам существуют только за этот промежуток времени.

Таблица 7. 1. Значения наблюдаемых величин.

Наблюдаемые величины	Значения
Номер недели, х
Количество проданных автомобилей, у

Смоделируем динамику продаж, которая имеет место, а на основе построенной модели попытаемся заглянуть в будущее, т.е. спрогнозировать ожидаемый объем продаж на ближайшие недели.

Пусть, х – номер недели и у – количество проданных за неделю автомобилей. В качестве модели возьмем простейшую, т.е. линейную.

Таким образом, необходимо построить линейную модель у = kх + b, наилучшим образом описывающую наблюдаемые значения. Обычно параметры k и b подбираются так, чтобы минимизировать сумму квадратов отклонений (разностей) теоретических (определенных по линейной модели) и наблюдаемых значений зависимой переменной (у). Следовательно, необходимо минимизировать целевую функцию:

где n — число наблюдений (в данном случае n = 6).

Для решения этой задачи:

1. Заполним, отведенные под наблюдаемые величины диапазон ячеек А2:В7.
2. Занесем переменные k и b в ячейкиD2 и Е2, соответственно.
3. Ячейки С2:С7 отведем под теоретические значения у. Для этого введем в С2 формулу линейной зависимости (выбранный вид зависимости), {=$D$3*A2+$E$3}. Затем скопируем ее до ячейки С7.
4. Задать целевую функцию можно несколькими способами.

Способ первый.

В ячейку F2 с помощью мастера функций (Категория Математические функция СУММКВРАЗН) введем целевую функцию {=СУММКВРАЗН(В2:В7;С2:С7)} как показано на рис.7.1.

Рис. 7. 1. Ввод целевой функции.

Способ второй.

В ячейку F2 с помощью мастера функций введем целевую функцию {=СУММ((B2:B7-D2*A2:A7-E2)^2)}. Это формула массива, поэтому не забудьте завершить ее ввод нажатием соответствующего сочетания клавиш.

1. С помощью Поиска решения (рис. 7.2.) необходимо минимизировать значение целевой ячейки F2, изменяя значения ячеек D3:E3. Отметим, что на переменные k и b ограничения не налагаются.

 

Рис. 7. 2. Построение линейной модели с помощью средства Поиск решения.

В результате вычислений механизм Поиска решений найдет следующие значения коэффициентов: k = 1,88571 и b = 5,400. (рис. 7.3.)

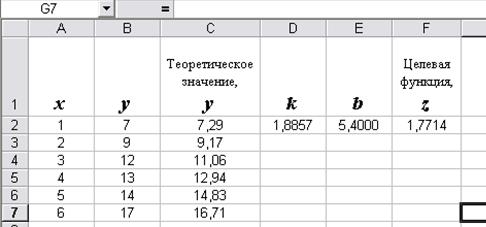
Рис. 7. 3. Результат построения линейной модели.

Таким образом, уравнение регрессии для данной задачи имеет вид:

у = 1,88571 * х + 5,400.