Будем рассматривать квазиравновесные процессы, т.е. такие, которые идут настолько медленно, что характерное время установления внутреннего равновесия 
много меньше времени наблюдения за протекающим процессом 
. К таким процессам может быть применено первое начало термодинамики. Проанализируем с этой точки зрения квазиравновесные процессы в идеальном газе, то есть процессы в системах, уравнением состояния которых является уравнение Менделеева-Клапейрона.
Пусть процесс идет без теплообмена с окружающей средой, то есть система является адиабатически изолированной. Процессы происходящие в такой системе, называются адиабатными процессами, при этом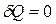 
. Для обеспечения этого условия процесс должен идти быстро. Противоречит ли это условию квазиравновесности процесса? Введем время установления равновесия системы с окружающей средой 
. О квазиравновесном адиабатном процессе можно говорить, только когда 
.
Предположим, что рассматриваемый процесс удовлетворяет указанному условию и, следовательно, к его анализу применимо первое начало термодинамики, которое в данном случае принимает вид
, (3.3.1)
т.е. при адиабатном процессе работа совершается системой за счет убыли ее потенциальной энергии, то
. (3.3.2)
Теплоемкость системы в адиабатном процессе равна нулю. Это относится к термодинамической системе любой природы.
Введем в рассмотрение идеальный газ, используем выражение (3.3.2) и уравнение состояния идеального газа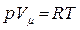 
Разделив переменные, получим
. (3.3.3)
После интегрирования уравнения (3.3.3) с учетом уравнения Майера (3.2.11) приходим к уравнению адиабаты в координатах (V,T), связывающему температуру и объем идеального газа в адиабатном процессе:
, (3.3.4)
где величина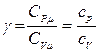 
называется показателем адиабаты и равна отношению молярных (или удельных) теплоемкостей газа при постоянном давлении и постоянном объеме.
Используя уравнение Менделеева - Клапейрона можно записать уравнение адиабаты через две другие пара параметров состояния
, (3.3.5)
. (3.3.6)
Найдем выражение для работы, совершаемой идеальным газом в адиабатном процессе при переходе из состояния 1 с параметрами 
в состояние 2 c параметрами 
.
. (3.3.7)
Поскольку численное значение работы и ее знак удобно определять по графику процесса, изображенного в координатах 
, адиабату часто изображают именно в этих координатах. На рис. 3.3.1 изображены изотерма и адиабата для равных масс идеального газа.
Большая крутизна адиабаты по сравнению с изотермой может быть объяснено из термодинамических представлений. Пусть изотермическое и адиабатное расширение начинаются из одного и того же состояния. В изотермическом процессе давление уменьшается за счет уменьшения объема, а в адиабатном процессе – за счет уменьшения объема и уменьшения средней кинетической энергии молекул, то есть быстрее, чем в изотермическом процессе. Рассуждая аналогично в случае начала изотермического и адиабатного сжатия из одного и того же состояния, приходим к выводу, что увеличение давления в адиабатном процессе идет медленнее.
Как можно показать, теплоемкость в изотермическом процессе равна бесконечности
при T = const, (3.3.8)
при постоянном давлении и при постоянном объеме теплоемкости имеют некоторые конечные значения
, 
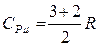, (3.3.9)
в адиабатном процессе теплоемкость равна нулю, т.к.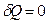 
.
Рассмотрим теперь процессы с промежуточными значениями теплоемкости, которая в течение процесса не изменяется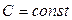 
. Процессы, идущие при постоянной теплоемкости, называются политропическими процессами. Пусть адиабатный процесс, совершаемый над одним молем идеального газа является квазиравновесным.
Согласно первому началу термодинамики для рассматриваемого случая получаем
, (3.3.10)
где 
при политропических процессах. С учетом 
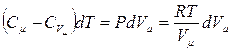, откуда 
.
Из уравнения Майера 
, следовательно
Величина 
называется показателем политропы. Тогда
. (3.3.11)
Интегрируя правую и левую части (метод разделения переменных), получим
или
(3.3.12)
- уравнение политропы. С помощью уравнения Менделеева-Клапейрона его можно записать в виде:
. (3.3.13)
. (3.3.14)
Очевидно, что
при С = 0; n = γ; 
— уравнение адиабаты;
при С = ∞; n = 1;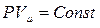 
— уравнение изотермы;
при С = Ср; n = 0; P = Const — уравнение изобары;
при C = Cv; n = 
; 
, но 
, следовательно, V = Const — уравнение изохоры.
Все изопроцессы являются частными случаями политропического процесса.
Работа при изопроцессах.
Изохорный процесс (V = сonst).
Так как система не изменяет своего объема, она не совершает работы над внешними телами
; А=0, тогда 
, (3.4.1)
При изохорном процессе работа газом не совершается, а поступающее (или отдаваемое) тепло равно изменению внутренней энергии.
Изобарный процесс (P=сonst).
При постоянном давлении объем системы меняется, и она может совершать работу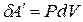 
,
. (3.4.2)
Используя уравнение состояния идеального газа 
(P = Const), можно записать
. (3.4.3)
Из I начала термодинамики
,
откуда
. (3.4.4)
При изобарическом процессе часть поступающего тепла расходуется на увеличение внутренней энергии, а часть – на совершение макроскопической работы.
Изотермический процесс (T = сonst)
При изотермическом процессе температура системы не меняется и, следовательно 
. Тогда из I начала термодинамики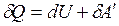 
, 
, т.е. 
, или Q = A΄. Из уравнения состояния идеального газа можно выразить Р: 
, тогда
и
. (3.4.5)
Следовательно,
.
При изотермическом процессе внутренняя энергия газа не меняется, вся полученная теплота идет на совершение работы.
Адиабатический процесс (
).
При адиабатическом процессе к системе не подводится теплота. В этом случае 
. Из уравнения адиабаты 
давление 
. Тогда 
и
. (3.4.6)
При адиабатическом процессе работа совершается газом за счет уменьшения его внутренней энергии.
Найдем выражение для вычисления работы в политропическом процессе. Будем использовать уравнение политропы в параметрах (p,V). Если известны значения давления и объема в некотором состоянии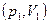 
, тогда
. (3.4.7.)
Покажем, что изотермический, изобарный, изохорный и адиабатный процессы являются частными случаями политропического процесса. В адиабатном процессе 
, следовательно 
и уравнения политропы (3.3.12), (3.3.13), (3.3.14) переходят в уравнения адиабаты в виде (3.3.4), (3.3.5) и (3.3.6) соответственно.
Теплоемкость при изотермическом процессе равна бесконечности, следовательно 
. Из уравнений (3.3.12) и (3.3.14) получаем условие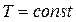 
, а выражение (3.3.13) переходит в закон Бойля-Мариотта 
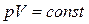. Показатель политропы в изобарном процессе равен нулю, поэтому из (3.3.12) получаем уравнение изобары 
. Для изохорного процесса показатель 
. Уравнение политропы (3.3.14) преобразуем к виду
, (3.4.8)
откуда получается уравнение изохоры 
.
Рассмотрим процесс не являющийся квазиравновесным – расширение газа в пустоту. Пусть имеется сосуд в адиабатически изолированной оболочке, разделенный на две части. В одной части давление 
и температура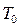 
, в другой части газа нет. Если перегородку убрать мгновенно, то возникает неравновесное состояние с потоками частиц, отличными от нуля. В дальнейшем, в процессе выравнивания параметров, потоки затухают и через некоторый промежуток времени в сосуде устанавливается равновесное состояние при температуре 
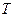. Так как перегородка убирается мгновенно, то газ не совершает работу против внешних сил; так как система адиабатически изолирована, количество теплоты газу не передается и не отнимается, следовательно, его внутренняя энергия не изменяется. В модели идеального газа, это означает, что температура газа остается постоянной.
К процессу расширения газа в пустоту нельзя применить результат, полученный для квазиравновесного процесса адиабатного расширения, для которого 
.
Применим полученные результаты к анализу процесса распространения звука в газах.
