ЗАКОНОМЕРНОСТИ РАВНОВЕСНОЙ ТЕРМОДИНАМИКИ
В некоторых ситуациях удобнее рассматривать поведение системы на основании термодинамического подхода. В настоящем разделе будет рассмотрена система начал равновесной термодинамики.
Первое начало термодинамики
Начнем рассмотрение данного вопроса с некоторых сведений из курса механики. При изучении неупругого удара было установлено, что в этом случае выполняется закон сохранения импульса и
. (3.1.1)
Но кинетическая энергия системы до удара больше кинетической энергии системы после удара:
, (3.1.2)
то есть закон сохранения механической энергии не выполняется. Другой пример: если тело скатывается по наклонной плоскости и далее катится по горизонтальной поверхности с трением, то через некоторое время тело останавливается. На что расходуется в рассмотренных ситуациях часть кинетической энергии? Она идет на нагревание тел, переходит во внутреннюю энергию. Этот переход совершается за счет работы, совершаемой против сил трения, и механическая энергия. В этом случае, в эквивалентном количестве переходит во внутреннюю энергию взаимодействующих тел, т.е. в теплоту.
Для объяснения механизма такого перехода высказывалась гипотеза о невесомой жидкости ‑ флагистоне, перетекающей из одного тела в другое. В середине XIX века Дж.П.Джоуль (Джеймс Прескотт Джоуль) опытным путем показал количественную эквивалентность теплоты и работы, что положило начало рассмотрению теплоты как работы, совершаемой на микроскопическом уровне, как микроскопической работы.
Вообще передача теплоты может происходить тремя способами: путем теплопередачи, конвекции и излучения. Последнее связано со сложным механизмом преобразования энергии электромагнитного поля в энергию атомов и молекул.
Обсудим подробнее понятие «внутренняя энергия». Энергия, которой обладает любая система, согласно специальной теории относительности, равна
. (3.1.3)
Если система движется как целое со скоростью v, то она обладает кинетической энергией 
Система, находящаяся в потенциальных полях, обладает, как целое, потенциальной энергией 
. Энергия системы 
в системе отсчета, связанной с центром масс рассматриваемой системы, находится как
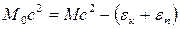. (3.1.4)
Эта энергия и определяет внутреннюю энергию системы U.
Подобное определение является общефизическим. Для выяснения физического смысла величины 
необходимо анализировать процессы, происходящие в молекулах, атомах, ядрах и т.д. Тогда
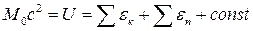, (3.1.5)
где суммирование производится по всем элементам системы, а постоянная характеризует энергию, сосредоточенную внутри элементов системы. С увеличением температуры, достигается такое ее значение, при котором начинается распад элементов (молекул, атомов, а затем и ядер). При этом величина константы изменяется, меняются и вклады других слагаемых, так как меняются сами элементы. В температурном интервале, в котором с атомами и ядрами никаких изменений не происходит, внутренняя энергия, с точностью до постоянной, связанной с введением нулевого уровня потенциальной энергии, определяется выражением
, (3.1.6)
здесь суммирование производится уже по всем молекулам системы.
Молекулы идеального газа взаимодействуют друг с другом только при соударениях, значит сумма потенциальных энергий их взаимодействия равна нулю и, следовательно, внутренняя энергия идеального газа определяется суммой кинетических энергий молекул
, (3.1.7)
где учтено выражение для средней кинетической энергии молекулы, не имеющей внутренних степеней свободы. Видно, что внутренняя энергия идеального газа пропорциональна температуре и зависит только от нее, т.е. значение внутренней энергии определяется только состоянием системы. Такие величины являются функциями состояния.
Внутреннюю энергию можно изменить двумя способами: путем совершения работы и в процессе теплопередачи. Энергию, переданную системе в процессе теплопередачи, называют количеством теплоты Q. Исторически сложилось так, что количество теплоты, переданное системе, принимается положительным, а отдаваемое - отрицательным.
В период господства теории теплорода, когда еще не было установлено, что при теплопередаче работа тоже производится, т.е. не только количество теплоты характеризует передаваемую телу энергию, была введена отдельная единица количества теплоты - калория. Одна калория равна тому количеству теплоты, которое нужно сообщить одному грамму воды, чтобы нагреть его от температуры 19,5 оС до 20,5 оС. Интервал температур конкретизируется, так как значение количества теплоты, необходимого для нагревания тела на один градус, зависит от диапазона температур. Естественно, что, как и любой другой вид энергии, количество теплоты может быть измерено в джоулях. 1 кал=4,9 Дж.
Конкретизируем понятие «термодинамическая работа». Начнем с рассмотрения элементарной работы идеального газа 
. Пусть газ расширяется в сосуде под невесомым поршнем.
При перемещении поршня на расстояние dx сила, действующая со стороны газа на поршень, совершает элементарную работу
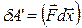. (3.1.8)
Работа совершается х -ой составляющей силы, эта составляющая оказывает давление на поршень, поэтому
, (3.1.9)
откуда, окончательно, получаем выражение для элементарной работы газа:
. (3.1.10)
Работа газа всегда связана с изменением объема. Она считается положительной при расширении газа и отрицательно при сжатии. В процессе расширения газ передает энергию окружающим телам, при сжатии получает энергию.
Очевидно, элементарная работа 
, совершаемая над газом внешними телами, отличается от работы газа только знаком.
Теперь, когда получены некоторые сведения о внутренней энергии, количестве теплоты и работе в термодинамике, сформулируем первое начало термодинамики. Внутренняя энергия термодинамической системы может быть изменена за счет сообщения ей количества теплоты и/или за счет совершения над системой работы:
. (3.1.11)
Первое начало можно записать в несколько ином виде, через работу газа:
. (3.1.12)
Количество теплоты, переданное системе, идет на изменение ее внутренней энергии и/или совершение системой работы.
Первое начало термодинамики является, подобно второму и третьему законам Ньютона, обобщением огромного количества опытных фактов и наблюдений. Область его применения не ограничивается только газами.
Прежде чем говорить о конкретных процессах, обратимся к вопросу о корректном описании термодинамического процесса вообще. Состояние равновесной системы характеризуется параметрами состояния. Задание набора параметров задает состояние системы. Количество параметров в наборе определяется уровнем сложности системы. В равновесном состоянии параметры не изменяются со временем и их можно отнести ко всей системе. Термодинамические процессы, разумеется, происходят при изменении параметров состояния. Можно ли ими характеризовать всю систему в целом? Относятся ли они ко всей системе? В термодинамике процессы считают происходящими бесконечно медленно, так, что отношение изменения объема к объему системы стремится к нулю при конечном интервале времени.
Рассмотрим для примера сжатие газа под поршнем. Сжатие происходит только вблизи поршня, изменение параметров распространяется в сосуде со скоростью звука, и за время 
устанавливается новое состояние равновесия, новые равновесные значения параметров состояния; 
характеризует время установления равновесного значения параметра (например, давления или температуры) при малом его изменении, т.е. это время, за которое изменение параметра распространяется на всю систему. Обозначим время протекания процесса через 
. Когда 
, в каждый момент времени любой параметр состояния можно отнести ко всей системе, а каждое состояние считать равновесным. Тогда процесс можно рассматривать как последовательную смену состояний, близких к равновесным. Такие процессы называют квазиравновесными процессами. Эта упрощенная модель позволяет получить выводы, важные как для термодинамики, так и для физики в целом.
Вычислим работу в квазиравновесном процессе. Работа равна сумме всех элементарных работ:
. (3.1.13)
Выражение (3.1.13), показывает, что работа газа численно равна площади под графиком процесса в координатах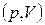 
. Изобразим произвольный круговой термодинамический процесс - цикл - в этих координатах (рис.3.1.2). Очевидно, что при переходе из точки А в точку В по пути А1В газ совершает большую работу, чем по пути А2В, так площадь криволинейной трапеции под графиком процесса в первом случае больше, чем во втором. Из этого следует, что работа не определяется состоянием системы, то есть не является функцией состояния, но является функцией процесса. Поскольку работу за цикл можно вычислить как сумму работ на участках А1В и В2А, с учетом знаков, то работа за цикл численно равна площади фигуры, ограниченной графиком цикла.
