Дифференциальные параметры диода

Дифференциальные параметры связывают между собой малые изменения вели­чин, определяющих работу диода. Ток в диоде является функцией двух независи­мых переменных — напряжения и и температуры T, поэтому дифференциал тока, то есть его приращение, имеет две составляющих;

Частные производные перед дифференциалами независимых переменных du и dT представляют собой дифференциальные параметры диода. Введем для них обо­значения:

□ дифференциальная крутизна вольт-амперной характеристики (пря­мая проводимость), мА/В;

□ дифференциальная температурная чувствительность тока диода,

Используя введенные обозначения, запишем соотношение (3.27) в виде

(3.28)

Если принять за независимые переменные ток i и температуру Т, то дифференци­ал напряжения можно представить в виде

(3.29)

В этом случае для дифференциальных параметров вводят обозначения:

□ — дифференциальное сопротивление диода, Ом;

□ — дифференциальная температурная чувствительность напряжения диода, мВ/°С.

Используя введенные обозначения, запишем соотношение (3.29) в виде

(3.30)

Переходя от бесконечно малых приращений к конечным, дифференциальные па­раметры можно определить по вольт-амперным характеристикам диода, снятым для двух значений температуры (рис. 3.7).

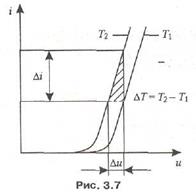
Дифференциальное сопротивление диода r_д содержит две составляющих:

где r_П — дифференциальное сопротивление р-п- перехода, зависящее от тока ди­ода;

r'₆ — дифференциальное сопротивление базы, зависящее от концентрации приме­си в базе.

Для нахождения сопротивления перехода продифференцируем уравнение вольт-амперной характеристики перехода:

Откуда получим:

(3.31)

Из (3.31) следует, что дифференциальное сопротивление р-n -перехода зависит от тока. С увеличением тока оно уменьшается. При Т = 300 К значение u равно 26 мВ. Следовательно, при токе i = 1 мА дифференциальное сопротивление р-n-перехода составляет 26 Ом.

Емкости диода

При рассмотрении процессов в р-n-переходе было установлено, что в самом переходе и в областях, прилегающих к переходу, существуют электрические заряды, которые изменяются при изменении подводимого к переходу напря­жения. Такое изменение зарядов воспринимается внешней цепью как электри­ческая емкость.

Барьерная емкость С_б характеризует изменение электрического заряда Q_ПЕР внут­ри перехода вследствие изменения его ширины Д при изменении внешнего напря­жения и:

Полагая, что р-п- переход несимметричен и в нем находится отрицательный заряд акцепторов, можно записать:

Учитывая, что , получаем:

(3.32)

Умножаем числитель и знаменатель дроби на εε₀ и, учитывая, что , получаем:

Ширина перехода Δ зависит от внешнего напряжения. При и = 0 величина Δ = Δ₀, С_б = С_0б. Если к переходу приложить обратное напряжение, то переход расши­рится и, соответственно, емкость уменьшится:

(3.33)

Соотношение (3.33) справедливо для резкого перехода. Если переход плавный, то барьерная емкость обратно пропорциональна не квадратному, а кубическому корню.

Диффузионная емкость С_Д характеризует изменение избыточного заряда, накап­ливаемого в областях, прилегающих к р-n-переходу, при изменении подводимого к переходу напряжения:

Концентрация примеси в эмиттере во много раз больше, чем в базе, поэтому в базу инжектируется больше неосновных носителей заряда, чем в эмиттер, и диффузи­онная емкость обусловлена только накоплением заряда в базе. Полагая, что база диода электронная, и учитывая, что в нее инжектируются дырки, концентрация которых уменьшается по мере удаления от перехода по экспоненциальному зако­ну, значение избыточного заряда можно определить, интегрируя изменение из­быточной концентрации по всей длине базы:

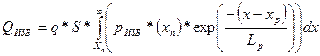(3.34)

Учитывая соотношение (1.94), получаем:

В результате дифференцирования имеем:

(3.35)

Умножая числитель и знаменатель дроби на τ_p, получаем:

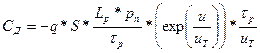
Учитывая, что ток диода равен , получаем:

(3.36)

Таким образом, диффузионная емкость прямо пропорциональна току.

При узкой базе диода избыточный заряд изменяется по линейному закону

Дифференцируя, получаем:

(3.37)

Умножим числитель и знаменатель дроби на W_б*D_р:

Учитывая, что ток диода , получаем:

(3.38)

Из соотношений (3.36) и (3.38) следует, что диффузионная емкость прямо про­порциональна току.