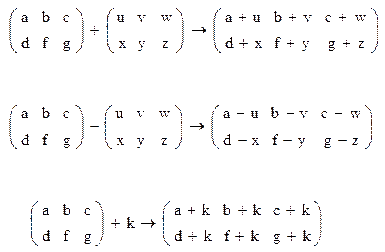Задания к лабораторной работе 2

Задание № 1

Постройте графики функций.

Вариант	Функция одной переменной	Полярная система координат	Функция двух переменных

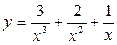
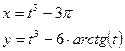
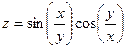
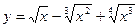
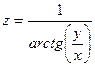
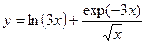
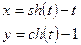
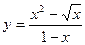
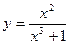
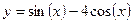
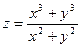
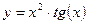
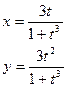
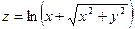
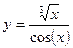
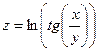
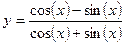
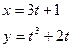
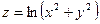
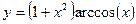
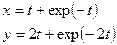
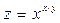
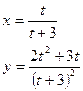
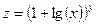
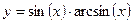
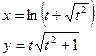
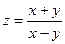
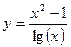
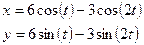
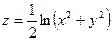
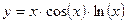
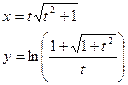
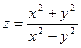
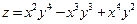
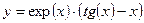
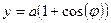
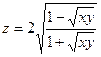
Задание № 2

Отобразить графически пересечение поверхностей и 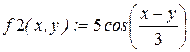. Матрицы для построения поверхностей задать с помощью функции CreateMesh.

Контрольные вопросы

1. Как построить график?

2. Как построить несколько графиков в одной системе координат?

3. Как построить декартовый график?

4. Как отформатировать построенный график?

5. Как построить график кривой, заданной параметрически?

6. Как построить график в полярной системе координат?

7. Как построить график поверхности?

8. Для чего используются функции CreateMesh, CreateSpace?

Лабораторная работа 3. Векторы и матрицы

Общие сведения

Задачи линейной алгебры, решаемые в MathCAD, можно условно разделить на два класса. Первый ‑ это простейшие матричные операции, которые сводятся к определенным арифметическим действиям над элементами матрицы. Они реализованы в виде операторов и нескольких специфических функций, предназначенных для создания, объединения, сортировки, получения основных свойств матриц и т. д. Второй класс ‑ это более сложные действия, которые реализуют алгоритмы вычислительной линейной алгебры, такие как вычисление определителей и обращение матриц, вычисление собственных векторов и собственных значений, решение систем линейных алгебраических уравнений и различные матричные разложения.

Простейшие операции матричной алгебры реализованы в MathCAD в виде операторов, причем их запись максимально приближена к математическому значению. Каждый оператор выражается соответствующим символом. Некоторые операции применимы только к квадратным матрицам N ´ N, некоторые допускаются только для векторов (например, скалярное произведение), а другие, несмотря на одинаковое написание, по-разному действуют на векторы и матрицы.

Создание матриц

Имеется два способа создать матрицу.

1-й способ. Использование команды создания массивов:

· Воспользоваться командой Вставка ® Матрица;

· нажатие клавиш Ctrl+M;

· выбор пиктограммы с изображением шаблона матрицы на панели инструментов Матрицы.

В диалоговом окне указать размерность матрицы, т. е. количество ее строк m (Rows) и столбцов n (Columns).

Для векторов один из этих параметров должен быть равен 1. При m = 1 получим вектор-столбец, а при n = 1- вектор-строку.

Далее на экране появится шаблон , в который нужно ввести значения элементов массива.

Обращаться к отдельным элементам вектора или матрицы можно используя нижний индекс. Для элемента матрицы указываются два индекса, один ‑ для номера строки, другой ‑ для номера столбца.

Чтобы ввести нижний индекс, нужно нажать клавишу [ после имени вектора или матрицы или выбрать команду на панели Матрицы.

2-й способ. Использование ранжированной переменной.

Ранжированная переменная используется для определения индекса (номера) элемента массива.

Например:

1) Создать матрицу В, состоящую из 2 строк и 3 столбцов.

2) Создать вектор S, состоящий из 3 элементов

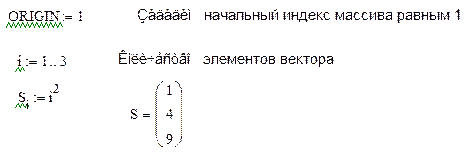
Команды панели инструментов Матрицы

Кнопка	Назначение
	Создание матрицы
	Обратная матрица
	Определитель матрицы
	Транспонирование матрицы
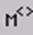
	Выделение столбца матрицы

Операторы для работы с массивами

Обозначения: для векторов ‑ V, для матриц ‑ М и для скалярных величин ‑ z.

Оператор	Ввод	Назначение оператора
V1+V2	V1+V2	Сложение двух векторов V1 и V2
V1-V2	V1-V2	Вычитание двух векторовV1 и V2
-М	-М	Смена знака у элементов матрицы M
V-z	V-z	Вычитание из вектора V скаляра z
zV, Vz	zV, Vz	Умножение вектора V на скаляр z
zM, Mz	zM, Mz	Умножение матрицы М на скаляр z
V1*V2	VI*V2	Умножение двух векторов V1 и V2
M*V	M*V	Умножение матрицы М на вектор V
М1*М2	М1*М2	Умножение двух матриц М1 и М2
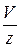
	V/z	Деление вектора V на скаляр z
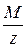
	M/z	Деление матрицы М на скаляр z
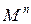
	М^n	Возведение матрицы М в степень п

Фрагмент документа MathCAD:

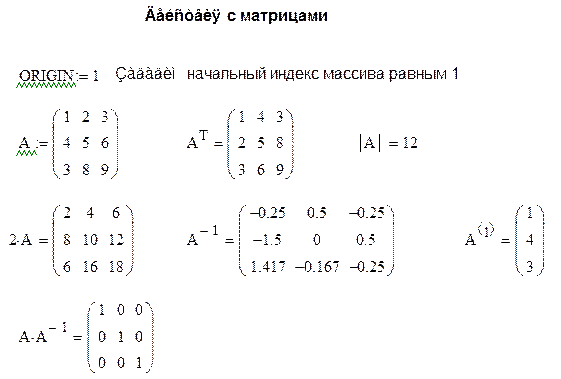
Функции для работы с векторами и матрицами.

Некоторые из них (V должен быть вектором, A может быть вектором либо матрицей):

length(V) ‑возвращает число элементов в векторе v;

last(V) ‑ возвращает индекс последнего элемента;

max(A) ‑ возвращает максимальный по значению элемент;

min(A) ‑ возвращает минимальный по значению элемент.

Матричные функции

Для работы с матрицами также существует ряд встроенных функций:

augment(M1, М2) ‑ объединяет в одну матрицы М1 и М2, имеющие одинаковое число строк;

identity(n) ‑ создает единичную квадратную матрицу размером 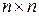, (n – размер матрицы(число));

stack(MI, M2) ‑ объединяет две матрицы М1 и M2, имеющие одинаковое число столбцов, сажая M1 над M2;

diag(V) ‑ создает диагональную матрицу, элемент главной диагонали которой ‑ вектор V;

cols(M) ‑ возвращает число столбцов матрицы М;

rows(M) ‑ возвращает число строк матрицы М;

rank(M) ‑возвращает ранг матрицы М;

tr(M) ‑ возвращает след (сумму диагональных элементов) квадратной матрицы М;

mean(M) ‑ возвращает среднее значение элементов массива М;

median(M) ‑ возвращает медиану элементов массива М;

eigenvals(M) ‑ возвращает вектор, элементами которого являются собственные значения матрицы M (M должна быть квадратной матрицей.);

submatrix(M,ir,jr,ic,jc) ‑ возвращает подмассив, состоящий из всех элементов, которые содержатся в строках с ir по jr и столбцах с ic по jc массива М.

Символьные вычисления

Все матричные и векторные операторы допустимо использовать как в численных, так и в символьных расчетах. Мощь символьных операций заключается в возможности проводить их не только над конкретными числами, но и над переменными.

Фрагмент документа MathCAD: