ДВУХ ПЕРЕМЕННЫХ
Задание 1
Найти и изобразить на рисунке область определения функции z = f(x,y).

Решение
Данная функция определена, если  или
или  . Таким образом, область определения функции находится внутри параболы.
. Таким образом, область определения функции находится внутри параболы.

Задание 2
Найти точки разрыва функции z = f(x,y). 
Решение
Точки разрыва функции будут наблюдаться там, где sin(πx) = 0 и sin(πу) = 0. Решая эти два уравнения, находим: х = у = 1, 2, 3,... Т.е. х є Z и у є Z.
Ответ: х є Z; у є Z.
Задание 3
Для функции z = f(x,y) найти указанные частные производные
 , z''xx-?, z''xу-?
, z''xx-?, z''xу-?
Решение
Имеем:
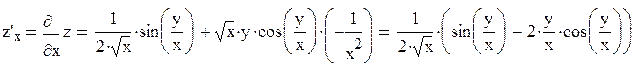


Задание 4
Вычислить значение производной сложной функции u = u(x,y), где x = x(t),
y = y(t), при t = t0с точностью до двух знаков после запятой.
 ,
,  ,
,  , t0= -1.
, t0= -1.
Решение
Если z = f(х;у) дифференцируемая в точке М(х;у) є D функция и х = x(t) и у = y(t) дифференцируемые функции независимой переменной t, то производная сложной функции z(t) = f(x(t);y(t)) вычисляется по формуле

Имеем:
 ;
;  ;
;  ;
;  .
.
Таким образом
 при t = -1
при t = -1  .
.
Ответ:  .
.
Задание 5
Вычислить значения частных производных функции z = z(x,y), заданной неявно, в данной точке М0(x0;y0;z0) с точностью до двух знаков после запятой.
 , М0(0;1;-1).
, М0(0;1;-1).
Решение
Обозначим  , тогда
, тогда  ,
,  . Находим:
. Находим:
 ,
, 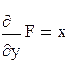 ,
,  . Тогда
. Тогда  ,
, 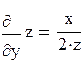 .
.
В точке М0 значения производных:  ,
, 
Ответ:,.
Задание 6
Найти приближенное значение данного выражения с помощью дифференциала.
0,972,02.
Решение
Рассмотрим функцию z = xy. Тогда 0,972,02 = (х + Δх)y+Δy, где х = 1; Δх = -0,03;
у = 2; Δу = 0,02. Воспользуемся формулой:
 . Находим
. Находим
 , z'x(1;2) = 2,
, z'x(1;2) = 2,  , z'y(1;2) = 0. Таким образом
, z'y(1;2) = 0. Таким образом
 .
.
Ответ: 0,94.
Задание 7
Найти grad(z) в точке А и производную функции z = f(x,y) в точке А по направлению вектора  .
.
 ; A(1;-1);
; A(1;-1); 
Решение
Градиентом функции z = f(x,y) называется вектор:  . Находим:
. Находим:
 ;
;  . В точке А(1;-1)
. В точке А(1;-1) 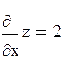 ,
,  . Таким образом:
. Таким образом: 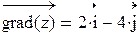 .
.
Производная функции z = f(x,y) по направлению вектора  имеет вид:
имеет вид:
 , где cos(α) и cos(β) - направляющие косинусы вектора
, где cos(α) и cos(β) - направляющие косинусы вектора  . Имеем:
. Имеем:  ,
,  . Таким образом, в точке A(1;-1)
. Таким образом, в точке A(1;-1)
 .
.
Ответ:;.
Задание 8
Составить уравнение касательной плоскости и уравнение нормали к заданной поверхности S в точке М0(x0;y0;z0).
S:  ; М0(1;1;1).
; М0(1;1;1).
Решение
Запишем данную функцию в виде:  . Уравнение касательной плоскости имеет вид:
. Уравнение касательной плоскости имеет вид:
 . Находим:
. Находим:
f(x0;y0) = f(1;1) = 1;  ; f'x(1;1) = -1;
; f'x(1;1) = -1;
 ; f'z(1;1) = 2,5.
; f'z(1;1) = 2,5.
Таким образом  или
или  .
.
Уравнение нормали имеет вид:  .
.
Подставляя найденные ранее значения для частных производных, получаем:
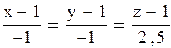
Задание 9
Исследовать на экстремум функцию z = f(x,y).

Решение
Найдем критические точки, для чего сперва найдем частные производные:
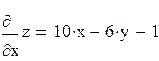 ;
;  . Решая систему:
. Решая систему:


находим точку M( ;
;  ).
).
Найдем производные второго порядка:
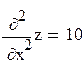 ;
;  ;
;  . Составим определитель:
. Составим определитель:
 .
.
Поскольку Δ > 0 и  , то в точке М функция z = f(x,y) принимает минимальное значение. zmin= z(
, то в точке М функция z = f(x,y) принимает минимальное значение. zmin= z( ;
;  ) =
) =  .
.
Ответ: zmin= z( ;
;  ) =
) =  .
.
Задание 10
Найти наибольшее и наименьшее значение функции z = f(x,y) в замкнутой области D. Сделать рисунок области D.
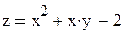 D:
D:  , y = 0.
, y = 0.
Решение
Изобразим область D.
Наибольшее или наименьшее значение функция z = f(x,y) может принять либо внутри области D, либо на ее границе. Найдем критические точки, для чего сперва найдем частные производные:
 ;
;  . Решая систему:
. Решая систему:


находим точку O(0;0). Поскольку данная критическая точка принадлежит границе области, то наибольшее и наименьшее значение функции также ищем на границе области.
На отрезке АC y = 0 и z = x2- 2. z' = 2x. Решая уравнение z' = 0, находим критическую точку: х = 0. О(0;0).
Вдоль параболы АВС  , а значит
, а значит  или
или  ,
, 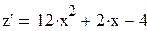 . Решая уравнение z' = 0, находим критические точки:
. Решая уравнение z' = 0, находим критические точки:  ,
,  . М(
. М( ;-3), N(
;-3), N(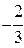 ;
;  ).
).
Таким образом, наибольшее и наименьшее значение функции ищем среди значений, которые принимает данная функция z = f(x,y) в точках О(0;0), А(-1;0), М( ;-3) и N(
;-3) и N(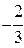 ;
;  ). Находим: z(0;0) = -2; z(-1;0) = z(1;0) = -1;
). Находим: z(0;0) = -2; z(-1;0) = z(1;0) = -1;
z(1;0) = -1; z( ;-3) =
;-3) =  ; z(
; z(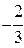 ;
;  ) =
) =  .
.
zmin= z( ;-3) =
;-3) =  ; zmax= z(
; zmax= z(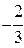 ;
;  ) =
) =  .
.
Ответ: zmin= z( ;-3) =
;-3) =  ; zmax= z(
; zmax= z(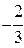 ;
;  ) =
) =  .
.




