РАЗДЕЛ I
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Задание 1
Найти общий интеграл дифференциального уравнения. (Ответ представить в виде ψ(х,у) = С).

Решение
Разделяя переменные в уравнении, имеем: 
Интегрируя обе части уравнения, получаем:

откуда 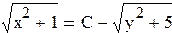 или
или 
Ответ: 
Задание 2
Найти общий интеграл дифференциального уравнения.

Решение
Разделим обе части уравнения на х. Имеем:

Введем замену: y = t∙x, тогда y' = t'∙x + t. Имеем

Разделяя переменные, получим

Интегрируя обе части уравнения, получаем:

откуда  или, после потенцирования,
или, после потенцирования,

Возвращаясь к замене, окончательно получаем: 2∙С∙х4= у3+ 3∙у∙х2
Ответ: 2∙С∙х4= у3+ 3∙у∙х2
Задание 3
Найти общий интеграл дифференциального уравнения.

Решение
Найдем точку пересечения прямых х + 2∙у - 3 = 0 и 4∙х - у - 3 = 0. Решая совместно эти два уравнения, находим: х = 1, у = 1.
Введем замены: y = v + 1, x = u + 1. Тогда dy = dv, dx = du. Имеем
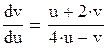 или
или 
Введем еще одну замену: v = t∙u, тогда v' = t'∙u + t. Имеем:
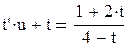
Разделяя переменные, получим: 
Интегрируя обе части уравнения, получаем:

откуда 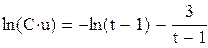 или, после потенцирования,
или, после потенцирования,
 .
.
Возвращаясь к заменам, окончательно получаем:  .
.
Ответ:.
Задание 4
Найти решение задачи Коши  ,
, 
Решение
Пусть  , тогда
, тогда  . Имеем:
. Имеем:
 или
или
 .
.
Пусть  тогда
тогда  .
.
Решим эти уравнения




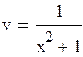
Подставим найденное значение в уравнение  :
:

 .
.
Возвращаясь к замене, окончательно получаем:
 .
.
При х = 0,  , т.е
, т.е 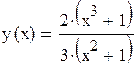
Ответ:.
Задание 5
Найти решение задачи Коши
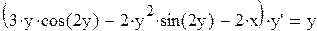 ,
, 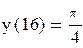
Решение
Примем у за независимую переменную, а х(у) - за функцию переменной у. Тогда по правилу нахождения производной обратной функции:  . Имеем:
. Имеем:
 или
или
 .
.
Пусть  , тогда
, тогда  . Имеем:
. Имеем:
 или
или
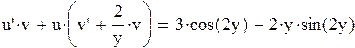 .
.
Пусть  тогда
тогда  .
.
Решим эти уравнения





Подставим найденное значение в уравнение
 :
:
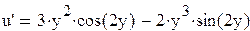
 .
.
Возвращаясь к замене, окончательно получаем:
 .
.
При  ,
,  т.е
т.е 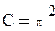 , а
, а 
Ответ:.
Задание 6
Найти решение задачи Коши: 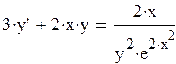 , y(0) = -1
, y(0) = -1
Решение
Пусть  , тогда
, тогда  , а
, а  . Имеем:
. Имеем:  . Умножим обе части уравнения на
. Умножим обе части уравнения на 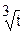 , получим:
, получим:
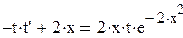 или
или  (1).
(1).
Решим однородное уравнение:  . Имеем:
. Имеем:  , откуда после интегрирования:
, откуда после интегрирования: 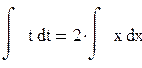 получаем
получаем  (2), где С(х) - неизвестная функция от х.
(2), где С(х) - неизвестная функция от х.
Подставляя (2) в (1), получаем:
 или
или
 . Интегрируя обе части уравнения, получаем:
. Интегрируя обе части уравнения, получаем:
 или
или
 , откуда
, откуда  . Подставляя полученное выражение в (2) получаем:
. Подставляя полученное выражение в (2) получаем:  .
.
Возвращаясь к замене, получаем:  .
.
При х = 0,  , откуда
, откуда  . Т.е.
. Т.е.
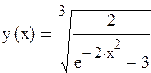 .
.
Ответ:.
Задание 7
Найти общий интеграл дифференциального уравнения.

Решение
Преобразуем данное уравнение. Имеем:

Введем замену: y = t∙x, тогда y' = t'∙x + t. Имеем

Разделяя переменные, получим
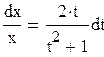
Интегрируя обе части уравнения, получаем:

откуда  или, после потенцирования,
или, после потенцирования,

Возвращаясь к замене, окончательно получаем: 
Ответ:.
Задание 8
Найти общее решение дифференциального уравнения:

Решение
Данное дифференциальное уравнениедопускает понижение порядка, поэтому принимаем y'' = t, тогда y''' = t'. Имеем:  . Разделяя переменные и интегрируя, получаем:
. Разделяя переменные и интегрируя, получаем:
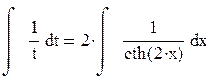 откуда
откуда  или
или
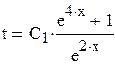 .
.
Возвращаясь к замене, получаем:
 ,
,

Ответ: 
Задание 9
Найти решение задачи Коши:  у(2) = 1, y'(2) = 6
у(2) = 1, y'(2) = 6
Решение
Данное дифференциальное уравнениене содержит явно переменную х. Введем замену: y'(x) = t(y), тогда  . Имеем:
. Имеем:
 . Разделяя переменные и интегрируя, получаем:
. Разделяя переменные и интегрируя, получаем:
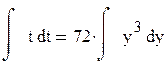 или
или 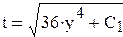 . При х = 2, у = 1,
. При х = 2, у = 1,  , откуда С1= 0. Т.е.
, откуда С1= 0. Т.е. 
Возвращаясь к замене, получаем: 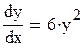 .
.
Разделяем переменные и интегрируем:  , откуда
, откуда  . При х = 2,
. При х = 2,  , откуда С2= -13. Таким образом:
, откуда С2= -13. Таким образом:  .
.
Ответ:.
Задание 10
Найти общее решение дифференциального уравнения:

Решение
Данному неоднородному уравнению четвертого порядка соответствует однородное уравнение  . Его характеристическое уравнение:
. Его характеристическое уравнение:  , корни которого
, корни которого
k1,2= 0, k3,4= -1. Поэтому, общее решение однородного уравнения имеет вид:  .
.
Частное решение неоднородного уравнения будем искать в виде:
 . Имеем:
. Имеем:
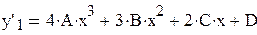 ;
; 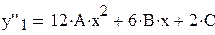 ;
;
 ; yIV1= 24A.
; yIV1= 24A.
Подставляя найденные значения в исходное уравнение, получаем:
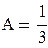 ,
,  , C = 12.
, C = 12.
Общее решение данного уравнения имеет вид:
 .
.
Ответ: 
Задание 11
Найти общее решение дифференциального уравнения:
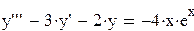
Решение
Данному неоднородному уравнению третьего порядка соответствует однородное уравнение  . Его характеристическое уравнение:
. Его характеристическое уравнение:  , корни которого k1,2= -1, k3= 2. Поэтому, общее решение однородного уравнения имеет вид:
, корни которого k1,2= -1, k3= 2. Поэтому, общее решение однородного уравнения имеет вид: 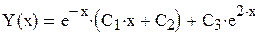 .
.
Частное решение неоднородного уравнения будем искать в виде:
 . Имеем:
. Имеем:
 ;
;
 ;
;
 .
.
Подставляя найденные значения в исходное уравнение, получаем: A = 0; B = 1; C = 0.
Общее решение данного уравнения имеет вид:
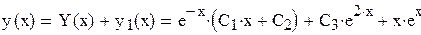 .
.
Ответ:.
Задание 12
Найти общее решение дифференциального уравнения:
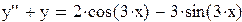
Решение
Данному неоднородному уравнению второго порядка соответствует однородное уравнение y'' + y = 0. Его характеристическое уравнение: k2 + 1 = 0, корни которого k1= -i, k2= i. Поэтому, общее решение однородного уравнения имеет вид:  .
.
Частное решение неоднородного уравнения будем искать в виде:
 . Имеем:
. Имеем:
 ;
;  .
.
Подставляя найденные значения в исходное уравнение, получаем:  ,
, 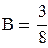 .
.
Общее решение данного уравнения имеет вид:
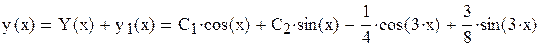 .
.
Ответ:.
Задание 13
Найти общее решение дифференциального уравнения:

Решение
Данному неоднородному уравнению второго порядка соответствует однородное уравнение y'' - 5y' = 0. Его характеристическое уравнение:
k2 - 5k = 0, корни которого k1 = 0, k2= 5. Поэтому, общее решение однородного уравнения имеет вид:  .
.
Частное решение неоднородного уравнения будем искать в виде:
 . Имеем:
. Имеем:
 ;
;
 .
.
Подставляя найденные значения в исходное уравнение, получаем: A = 5, B = 0, C = 5, D = -1.
Общее решение данного уравнения имеет вид:
 .
.
Ответ:.
Задание 14
Найти решение задачи Коши:
 y(0) = 1 + 3ln(3), y'(0) = 10ln(3)
y(0) = 1 + 3ln(3), y'(0) = 10ln(3)
Решение
Данному неоднородному уравнению второго порядка соответствует однородное уравнение  . Его характеристическое уравнение:
. Его характеристическое уравнение:  , корни которого k1 = 2, k2= 4. Поэтому, общее решение однородного уравнения имеет вид:
, корни которого k1 = 2, k2= 4. Поэтому, общее решение однородного уравнения имеет вид:  .
.
Запишем данное решение в виде:  . Найдем производные:
. Найдем производные:
 ,
,  .
.
Составляем систему:


Определитель системы: 
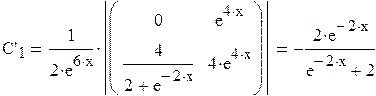
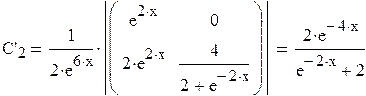


Таким образом  .
.
Решим задачу Коши, для чего сперва найдем производную:
 .
.
При х = 0, у = С1+ С2+ 3ln(3) - 1 = 1 + 3ln(3),
y' = 10ln(3) + 2C1+ 4C2- 2 = 10ln(3).
Имеем: С1+ С2= 2, 2C1+ 4C2= 2, откуда С1= 3, С2= -1. Таким образом:
 .
.
Ответ:.
РАЗДЕЛ II
ЧИСЛОВЫЕ И ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Задание 1
Написать пять первых членов ряда. Проверить для данного ряда выполнение необходимого признака сходимости. 
Решение

Для числового ряда  необходимый признак записывается в виде:
необходимый признак записывается в виде:  .
.
Применяя данный признак к нашему ряду, получаем:  , т.е. признак выполняется.
, т.е. признак выполняется.
Ответ: признак выполняется.
Задание 2
Исследовать ряд на сходимость с помощью признака сравнения: 
Решение
Для сравнения возьмем ряд  . Этот ряд сходится, как ряд геометрической прогрессии со знаменателем
. Этот ряд сходится, как ряд геометрической прогрессии со знаменателем 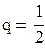 . В связи с тем, что
. В связи с тем, что  для х є (-∞;∞), приходим к выводу, что
для х є (-∞;∞), приходим к выводу, что  сходится для х є (-∞;∞).
сходится для х є (-∞;∞).
Ответ: ряд сходится.
Задание 3
Исследовать ряд на сходимость с помощью признака Даламбера: 
Решение
Согласно признаку Даламбера, если существует 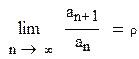 , то
, то
при ρ < 1 ряд сходится, при ρ > 1 ряд расходится, при ρ = 1 ряд может сходиться или расходиться. Имеем:
 ,
, 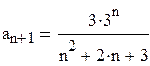 . Тогда
. Тогда  .
.
То есть, согласно признаку, ряд расходится.
Ответ: ряд расходится.
Задание 4
Исследовать ряд на сходимость с помощью интегрального (Коши-Маклорена) признака:

Решение
Согласно интегральному признаку, если:
1) члены ряда составляют монотонную невозрастающую последовательность
 ;
;
2) можно построить монотонную невозрастающую функцию y = f(x) такую, что
f(0) = a0; f(1) = a1;...; f(n) = an;...,
то если  сходится, тогда заданный ряд также сходится. Если же интеграл расходится, то и ряд расходится.
сходится, тогда заданный ряд также сходится. Если же интеграл расходится, то и ряд расходится.
Члены нашего ряда составляют монотонную последовательность

Следовательно, функцией f(x) будет  ;
; 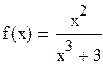 .
.  .
.
То есть, согласно признаку, ряд расходится.
Ответ: ряд расходится.
Задание 5
Записать общий член ряда: 
Решение
Данный ряд является знакочередующимся. Поскольку в числителе стоит порядковый номер члена ряда, а в знаменателе порядковый номер является показателем степени числа 2, то общий член ряда имеет вид: 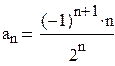 .
.
Ответ:.
Задание 6
Определить область сходимости функционального ряда: 
Решение
Построим ряд  . Для определения области сходимости последнего ряда воспользуемся признаком Даламбера:
. Для определения области сходимости последнего ряда воспользуемся признаком Даламбера:
 .
.
Ряд сходится, если  или -1 < x < 1, а значит и исходный ряд сходится абсолютно для х є (-1;1).
или -1 < x < 1, а значит и исходный ряд сходится абсолютно для х є (-1;1).
Ответ: (-1;1).
Задание 7
Разложить f(x) в ряд Тейлора по степеням разности х - х0, пользуясь определением ряда Тейлора.  , x0= 4.
, x0= 4.
Решение
Выражение  называется рядом Тейлора функции f(x) в окрестности точки x0. Найдем значения членов ряда:
называется рядом Тейлора функции f(x) в окрестности точки x0. Найдем значения членов ряда:
 ;
;  ;
;  . Имеем:
. Имеем:


Задание 8
Найти решение данного дифференциального уравнения в виде степенного ряда (четыре ненулевых члена).  , y(0) = 0
, y(0) = 0
Решение
Решение данного дифференциального уравнения будем искать в виде ряда Маклорена:
 .
.
Имеем:  ;
;
 ,
,  ;
;
 ,
,  ;
;
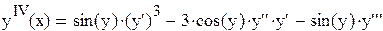 ,
,  .
.
Итак, четыре первых разложения имеют вид: 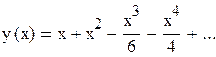
Ответ: 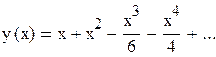
Задание 9
Найти неопределенный интеграл 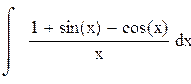
Решение
Поскольку интегралы от функций  и
и 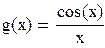 не выражаются через элементарные функции, будем искать выражение данного интеграла через степенные ряды. Для этого разложим sin(x) и cos(x) в ряд Маклорена. Имеем:
не выражаются через элементарные функции, будем искать выражение данного интеграла через степенные ряды. Для этого разложим sin(x) и cos(x) в ряд Маклорена. Имеем:
 ,
,
 .
.
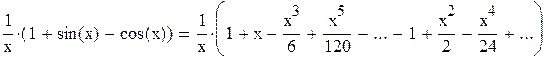 =
=
= 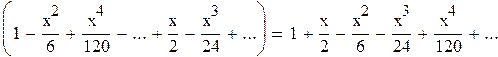
Таким образом:
 =
=
= 
РАЗДЕЛ III






