Построить вариационный ряд для случайной величины Х, построить интервальный вариационный ряд.
Вариационный ряд

| |||||||
Частота

|
Ищем диапазон и шаг
| n:=60 |
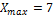
|

|

|
| R= 7 |

|
| h=1,01 |
Выбираем шаг, равный 1
Интервальный вариационный ряд
| № | Интервал | Частота mi | Частотность pi | Середина интервала X* |
| 0-1 | 0, 417 | 0,5 | ||
| 1-2 | 0,267 | 1,5 | ||
| 2-3 | 0,167 | 2,5 | ||
| 3-4 | 0,1 | 3,5 | ||
| 4-5 | 0,033 | 4,5 | ||
| 5-6 | 5,6 | |||
| 6-7 | 0,016 | 6,5 | ||
Построить полигон, гистограмму относительных частот, график эмпирической функции распределения для интервального вариационного ряда.
Полигон относительных частот
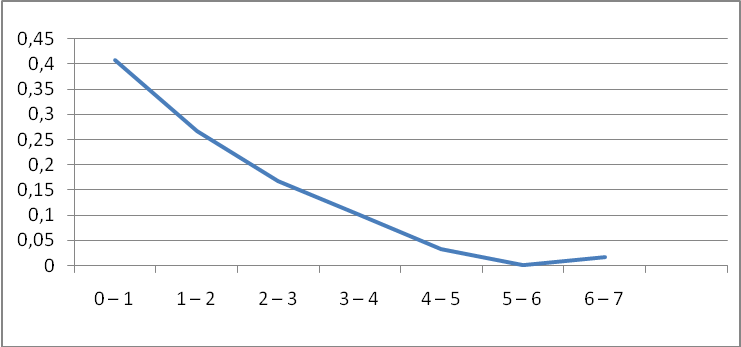
Гистограмма относительных частот

График эмпирической функции распределения для интервального вариационного ряда
3. Найти выборочные характеристики:
A) Объем выборки, выборочное среднее, выборочную дисперсию, исправленную дисперсию, среднее квадратическое отклонение, эксцесс, асимметрию, медиану и моду;
Выборочные характеристики:
Объём выборки n = 60
Выборочная средняя
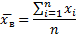

Выборочная дисперсия

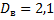
Выборочное среднее квадратическое отклонение

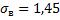
«Исправленная» дисперсия


«Исправленное» среднее квадратическое отклонение


Эксцесс


Асимметрия
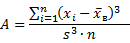

Медиана
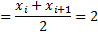
Мода
B) Доверительный интервал для среднего при неизвестной дисперсии, если случайная величина подчиняется нормальному закону распределения;
 ;
;  ;
; 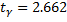


C) Доверительный интервал для дисперсии и среднего квадратического отклонения, если случайная величина подчиняется нормальному закону распределения;
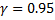 ;
;  ;
; 

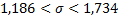

4. Проверка нулевой гипотезы о равенстве неизвестной генеральной средней a гипотетическому значению a0.



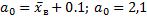

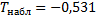


 => нет оснований отвергнуть нулевую гипотезу.
=> нет оснований отвергнуть нулевую гипотезу.
5. Проверка нулевой гипотезы о равенстве неизвестной генеральной дисперсии σ2 нормальной совокупности гипотетическому значению σ02.

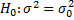

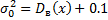



 43.2
43.2

 => нет оснований отвергать нулевую гипотезу.
=> нет оснований отвергать нулевую гипотезу.
По критерию согласия Пирсона проверить гипотезу о нормальности распределения генеральной совокупности.
Интервальный вариационный ряд
| № п/п | Интервал | Частота

| Частотность

| Середина интервала

|
| 0 – 1 | 0,417 | 0.5 | ||
| 1 – 2 | 0,267 | 1.5 | ||
| 2 – 3 | 0,167 | 2.5 | ||
| 3 – 7 | 0,149 |
 =2
=2
 =2,1
=2,1
 =1,45
=1,45
Вычисляем концы интервала ( ;
;  )
)
| i | Границы интервала | 
| 
| Границы интервала | ||
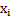
| 
| 
| 
| |||
| - | -1 | -∞ | -0,689 | |||
| -1 | -0,689 | |||||
| 0.689 | ||||||
| - | 0.689 | ∞ |
Вычисление теоретической вероятности t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>i</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  попадания Х в интервал (t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>i</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
попадания Х в интервал (t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>i</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  ;
; 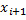 )
)
| i | 
| 
| Ф 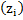
| Ф 
|  Ф Ф  Ф Ф 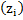
|  =n =n 
|
| -∞ | -0,689 | -0,5 | -0,2549 | 0,2451 | 14,706 | |
| -0,689 | -0,2549 | 0,2549 | 15,294 | |||
| 0.689 | 0,2549 | 0,2549 | 15,294 | |||
| 0.689 | ∞ | 0,2549 | 0,5 | 0,2451 | 14,706 | |
 1 1
|  0 0
|
Проверка гипотезы о нормальном распределении генеральной совокупности
| i |

| 
|  - - 
| 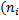 - -  )2 )2
| 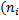 - -  )2/ )2/ 
|  2 2
|  2/ 2/ 
|
| 14,706 | -10,294 | 105,966 | 7,206 | 42,499 | |||
| 15.294 | 0.706 | 0.498 | 0,033 | 16.738 | |||
| 15.294 | -5.294 | 28.026 | 1.832 | 6.538 | |||
| 14,706 | -5.706 | 32.558 | 2.214 | 5.508 | |||

| X2 набл= 11.285 | 71.283 |
По таблице точек распределения, по уровню значимости α=0,05 и числу степеней свободы κ=1 находим X2 кр (0,05;1)= 3.8
Так как X2 набл > X2 кр- отвергаем нулевую гипотезу.






