Необходимо научиться управлять изображением на экране, вносить изменения в его положение, форму, ориентацию, размер. Для этих целей существует набор геометрических преобразований, которые позволяют изменять эти характеристики объектов в пространстве. Представим задачу создания компьютерного имитатора полетов на самолете. Будем считать, что перспективная проекция трехмерных объектов должна рассчитываться как вид из кабины пилота. Объекты на земле, которые видит пилот, изменяют свое положение. Например, автомобиль движется относительно земли, колеса автомобиля вращаются. При этом, наблюдатель видит эту картину из определенной точки в пространстве в выбранном направлении. Необходимо описать эти сложные преобразования математически.
Введем три вида систем координат. Первая из них – мировая система координат – задается осями 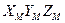 . Мы размещаем ее в некоторой точке, и она остается неподвижной всегда. Вторая – система координат наблюдателя. Эту систему назовем
. Мы размещаем ее в некоторой точке, и она остается неподвижной всегда. Вторая – система координат наблюдателя. Эту систему назовем  . Она определяет положение наблюдателя в пространстве и задает направление взгляда. И третья – система координат объекта. В нашем случае их две: система координат автомобиля и система координат его колес. Эти системы могут перемещаться и изменять свое положение в пространстве относительно мировой системы координат. Координаты точек объектов задаются в системах координат объектов, каждая из которых, в свою очередь, привязана к мировой системе координат. Система координат наблюдателя также перемещается относительно мировой системы координат. Теперь становится понятно, что для того, чтобы увидеть трехмерный объект на экране компьютера надо проделать следующие шаги.
. Она определяет положение наблюдателя в пространстве и задает направление взгляда. И третья – система координат объекта. В нашем случае их две: система координат автомобиля и система координат его колес. Эти системы могут перемещаться и изменять свое положение в пространстве относительно мировой системы координат. Координаты точек объектов задаются в системах координат объектов, каждая из которых, в свою очередь, привязана к мировой системе координат. Система координат наблюдателя также перемещается относительно мировой системы координат. Теперь становится понятно, что для того, чтобы увидеть трехмерный объект на экране компьютера надо проделать следующие шаги.
1. Преобразовать координаты объекта, заданные в собственной системе координат, в мировые координаты.
2. Преобразовать координаты объекта, заданные уже в мировой системе координат, в систему координат наблюдателя.
3. Спроецировать полученные координаты на проекционную плоскость в системе координат наблюдателя.
В библиотеках компьютерной графики, таких как OpenGL и Direct3D, приведенные здесь типы преобразований задаются в виде матриц и имеют собственные устоявшиеся названия. Первое преобразование называется мировым, соответствующая матрица мирового преобразования (WORLD MATRIX). Второе преобразование называется модельным или видовым и определяется матрицей модельного или, соответственно, видового преобразования (VIEW MATRIX). Третье преобразование называется преобразованием проекции и соответствующая матрица – матрицей проецирования (PROJECTION MATRIX).
Отметим, определенную двойственность, возникающую при взаимных перемещениях систем координат друг относительно друга. Представим себе, что мы наблюдаем кубик в пространстве. Пусть этот кубик начнет вращаться, например, вокруг вертикальной оси. Мы увидим, что кубик вращается. Но тот же самый эффект мы получим, если сами начнем облетать вокруг кубика и рассматривать его с разных сторон. Визуальный эффект остается тем же самым, хотя в первом случае наша система координат остается неподвижной, а во втором – вращается по орбите. Этот эффект можно использовать при выводе формул движения в пространстве.






