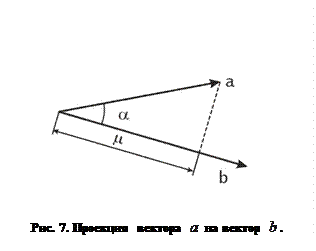
Иногда бывает необходимо вычислить длину проекции радиус-вектора не на ось системы координат, а на другой радиус-вектор. Найдем длину проекции вектора 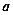 на вектор
на вектор 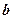 . Эта ситуация изображена на рис. 7, из которого, очевидно, следует и решение задачи.
. Эта ситуация изображена на рис. 7, из которого, очевидно, следует и решение задачи.
 Искомая проекция:
Искомая проекция: 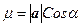 =
=  =
= 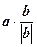 .
.
В случае тупого угла между векторами a и b значение  в данном выражении будет отрицательным. Поэтому для получения длины проекции следует взять
в данном выражении будет отрицательным. Поэтому для получения длины проекции следует взять 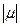 .
.
Как видно, если длина вектора, на который проецируется другой вектор, равна единице, то длина проекции будет просто равна скалярному произведению этих векторов.
С помощью формулы длины проекции вектора на вектор можно еще одним способом получить уравнение плоскости, если заметить, что длины проекций радиус-векторов, принадлежащих плоскости, на вектор нормали к плоскости всегда равны между собой.
Рассмотрим задачу нахождения минимального расстояния от начала координат до плоскости. Очевидно, что это расстояние необходимо откладывать вдоль прямой, определяемой вектором нормали к плоскости. Но для нахождения этого расстояния надо найти сначала точку пересечения прямой с плоскостью. Поэтому найдем вначале решение задачи нахождения точки пересечения прямой и плоскости. Обозначим искомую точку, или соответствующий ей радиус-вектор x. Тогда эта точка должна одновременно удовлетворять уравнениям прямой и плоскости, например, 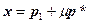 и
и 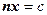 , где
, где  и
и  – базовый и направляющий векторы, а
– базовый и направляющий векторы, а  – вектор нормали к плоскости. Подставив x из первого уравнения во второе, найдем значение константы
– вектор нормали к плоскости. Подставив x из первого уравнения во второе, найдем значение константы  , которое затем подставим в исходное уравнение прямой для получения координат искомой точки:
, которое затем подставим в исходное уравнение прямой для получения координат искомой точки:
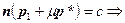
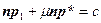

Уравнение прямой вдоль вектора нормали к плоскости запишем как 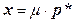 , так как прямая проходит через начало координат и базовый вектор
, так как прямая проходит через начало координат и базовый вектор  равен нулю. Перед тем как подставить в это уравнение выражение для
равен нулю. Перед тем как подставить в это уравнение выражение для  , заметим, что направляющий вектор совпадает с вектором нормали
, заметим, что направляющий вектор совпадает с вектором нормали 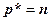 . Учитывая это, запишем:
. Учитывая это, запишем:
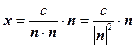
Отсюда искомое расстояние от начала координат до плоскости равно
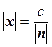
В том случае, когда вектор нормали  является нормированным, т.е. его длина равна 1, константа
является нормированным, т.е. его длина равна 1, константа 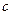 в уравнении плоскости равна расстоянию от начала координат до данной плоскости.
в уравнении плоскости равна расстоянию от начала координат до данной плоскости.
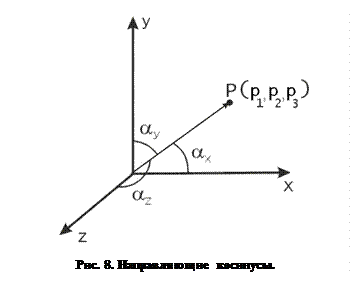
Кроме определения положения точек в пространстве радиус-векторы также определяют направление в пространстве. Направление, определяемое радиус-вектором, удобно описывать с помощью, так называемых, направляющих косинусов. Пусть радиус-вектор 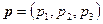 составляет с осями координат
составляет с осями координат  ,
,  и
и  углы, соответственно,
углы, соответственно, 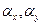 и
и 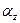 (рисунок 8). Тогда его направляющие косинусы равны:
(рисунок 8). Тогда его направляющие косинусы равны:
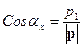 ,
, 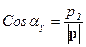 ,
, 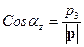
Отсюда, очевидно, вытекают следующие свойства направляющих косинусов:
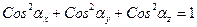 .
.
Направляющие косинусы пропорциональны соответствующим координатам:
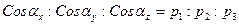 ,
,
а в случае, когда вектор 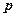 нормирован, значения его координат равны соответствующим направляющим косинусам.
нормирован, значения его координат равны соответствующим направляющим косинусам.
Уравнение плоскости можно представить как функцию трех переменных. Для этого в уравнении (5) перенесем константу из правой части в левую и запишем функцию трех переменных 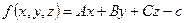 . Если подставить координаты точки, принадлежащей данной плоскости, в это уравнение, то
. Если подставить координаты точки, принадлежащей данной плоскости, в это уравнение, то 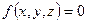 . Если же точка не принадлежит плоскости, то значение функции, очевидно, будет больше или меньше нуля. Интересен тот факт, что для точек, лежащих по одну и ту же сторону от плоскости, функция
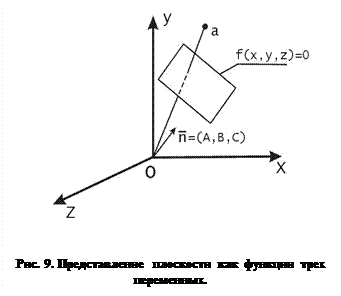
. Если же точка не принадлежит плоскости, то значение функции, очевидно, будет больше или меньше нуля. Интересен тот факт, что для точек, лежащих по одну и ту же сторону от плоскости, функция 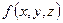 имеет всегда один и тот же знак. С помощью чертежа на рисунке 9, можно показать, что для точек, лежащих в полупространстве, порождаемом плоскостью и содержащем начало координат, функция
имеет всегда один и тот же знак. С помощью чертежа на рисунке 9, можно показать, что для точек, лежащих в полупространстве, порождаемом плоскостью и содержащем начало координат, функция 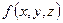 отрицательна, а для точек, лежащих в другом полупространстве, как, например, для точки
отрицательна, а для точек, лежащих в другом полупространстве, как, например, для точки 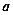 на рисунке, она положительна. В общем же случае необходимо учитывать направление вектора нормали.
на рисунке, она положительна. В общем же случае необходимо учитывать направление вектора нормали.
 Свойство сохранения знака функции
Свойство сохранения знака функции 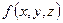 удобно использовать в алгоритмах удаления невидимых ребер и граней для определения того, лежат ли точки по одну сторону от плоской грани или нет. Для этого достаточно лишь подставить значения координат точек в функциональное представление плоскости, определяемой соответствующей гранью, и проверить, совпадают знаки функции или нет. Аналогичные рассуждения можно провести и для более простого случая прямой на плоскости. Тогда для любой точки на плоскости можно определить ее нахождение в одной из полуплоскостей, на которые прямая делит плоскость. Это свойство используется в следующем примере.
удобно использовать в алгоритмах удаления невидимых ребер и граней для определения того, лежат ли точки по одну сторону от плоской грани или нет. Для этого достаточно лишь подставить значения координат точек в функциональное представление плоскости, определяемой соответствующей гранью, и проверить, совпадают знаки функции или нет. Аналогичные рассуждения можно провести и для более простого случая прямой на плоскости. Тогда для любой точки на плоскости можно определить ее нахождение в одной из полуплоскостей, на которые прямая делит плоскость. Это свойство используется в следующем примере.
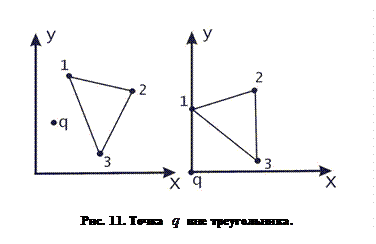
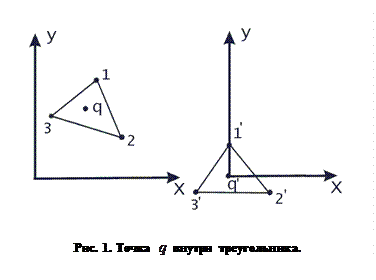
Рассмотрим методы решения классической задачи определения принадлежности точки внутренней или граничной области треугольника на плоскости. Эта задача имеет, конечно, много решений, некоторые из которых может придумать и сам читатель. Здесь приводится четыре из более чем двадцати методов решения этой задачи, известных автору. Лучшим из них может считаться метод, допускающий самую быструю программную реализацию, и в первую очередь это относится к минимизации количества операций умножения и деления, не говоря уже о трансцендентных функциях, вроде квадратного корня или тригонометрических функций, для вычисления которых требуется разложение в ряд. В начале рассмотрим один из известных методов решения этой задачи.
Пусть на плоскости 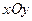 заданы три точки
заданы три точки 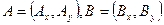 и
и 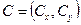 , образующие треугольник (рис. 10).
, образующие треугольник (рис. 10). 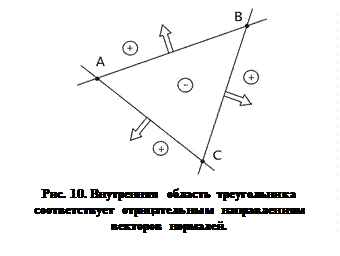 Через каждую пару вершин треугольника можно провести прямую. Ограниченная часть плоскости, образованная этими прямыми, есть внутренняя область треугольника. Если вектор нормали к прямой
Через каждую пару вершин треугольника можно провести прямую. Ограниченная часть плоскости, образованная этими прямыми, есть внутренняя область треугольника. Если вектор нормали к прямой 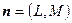 , то можно записать уравнение прямой на плоскости в виде:
, то можно записать уравнение прямой на плоскости в виде: 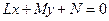 . По знаку функции
. По знаку функции 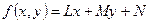 можно определить нахождение произвольной точки с координатами
можно определить нахождение произвольной точки с координатами 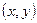 в той или иной полуплоскости относительно данной прямой. Идея первого метода состоит в том, чтобы записать функциональные представления уравнений прямых, образующих стороны треугольника, таким образом, чтобы внутренняя область треугольника соответствовала, например, отрицательным значениям. Тогда условием принадлежности внутренней области треугольника будут отрицательные значения трех функциональных уравнений прямых при подстановке координат проверяемой точки. Основной проблемой в этом методе является правильный выбор направления вектора нормали к прямой.
в той или иной полуплоскости относительно данной прямой. Идея первого метода состоит в том, чтобы записать функциональные представления уравнений прямых, образующих стороны треугольника, таким образом, чтобы внутренняя область треугольника соответствовала, например, отрицательным значениям. Тогда условием принадлежности внутренней области треугольника будут отрицательные значения трех функциональных уравнений прямых при подстановке координат проверяемой точки. Основной проблемой в этом методе является правильный выбор направления вектора нормали к прямой.
Следующий метод, разработанный автором в 1991 году, основан на преобразовании треугольника с помощью операции переноса таким образом, чтобы проверяемая точка совпала с началом координат. Поворотом плоскости вокруг начала координат расположим одну (любую) из вершин треугольника на оси  . Тогда если знаки координат
. Тогда если знаки координат  оставшихся двух точек совпадают, то искомая точка лежит вне треугольника. Если же знаки различны, то берем следующую из оставшихся вершин треугольника и поворотом плоскости устанавливаем ее на ось
оставшихся двух точек совпадают, то искомая точка лежит вне треугольника. Если же знаки различны, то берем следующую из оставшихся вершин треугольника и поворотом плоскости устанавливаем ее на ось  . После чего вновь проверяем знаки координат
. После чего вновь проверяем знаки координат  двух других вершин, и т.д.
двух других вершин, и т.д.
Условием принадлежности точки внутренней области треугольника будет несовпадение знаков  ‑ координат оставшихся двух вершин после каждого из трех поворотов.
‑ координат оставшихся двух вершин после каждого из трех поворотов.
 |
Нахождение точки на одной из сторон треугольника легко определяется по несовпадению знаков
 -координат двух вершин, которые после одного из поворотов оказались лежащими на оси
-координат двух вершин, которые после одного из поворотов оказались лежащими на оси  . Этот метод эффективен, когда больше вероятность, что точка лежит вне треугольника. Отрицательной его чертой является необходимость вычисления синусов и косинусов углов при повороте системы координат.
. Этот метод эффективен, когда больше вероятность, что точка лежит вне треугольника. Отрицательной его чертой является необходимость вычисления синусов и косинусов углов при повороте системы координат.
Третий из приводимых здесь методов до 2005 года считался мною одним из наиболее компактных и скоростных с вычислительной точки зрения. Этот метод был предложен автору Д. Чистяковым в 1999 году. Заметим, что очень просто можно определить принадлежность точки внутренней области треугольника – единичного симплекса, то есть треугольника, образованного точками с координатами 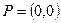 ,
, 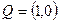 ,
, 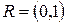 . Для этого достаточно чтобы координаты искомой точки имели значения в отрезке
. Для этого достаточно чтобы координаты искомой точки имели значения в отрезке 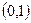 , и выполнялось условие
, и выполнялось условие 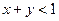 , где
, где 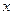 и
и 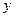 ‑ координаты точки. Заметим также, что с помощью аффинных преобразований и операций переноса или непрерывных деформаций любой треугольник можно преобразовать к единичному симплексу.
‑ координаты точки. Заметим также, что с помощью аффинных преобразований и операций переноса или непрерывных деформаций любой треугольник можно преобразовать к единичному симплексу.
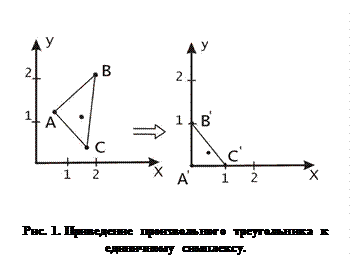 |
После таких преобразований внутренняя и внешняя области треугольника остаются таковыми. Применив такое преобразование к искомой точке, достаточно затем будет определить ее нахождение во внутренней или внешней области симплекса. Найдем такое преобразование. Координаты векторов единичного базиса совпадают с координатами точек
 и
и  симплекса, соответственно. Будем считать, что точка
симплекса, соответственно. Будем считать, что точка  треугольника совпадает с началом координат. Этого всегда можно добиться параллельным переносом треугольника на вектор
треугольника совпадает с началом координат. Этого всегда можно добиться параллельным переносом треугольника на вектор  . При этом координаты точек
. При этом координаты точек  и
и  треугольника суть коэффициенты разложения соответствующих векторов
треугольника суть коэффициенты разложения соответствующих векторов 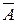 и
и 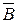 по единичному базису. Матрица преобразования
по единичному базису. Матрица преобразования 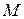 от единичного базиса к базису на векторах
от единичного базиса к базису на векторах 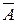 и
и 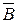 составлена из координат этих векторов.
составлена из координат этих векторов.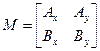
Значит, для обратного перехода к единичному базису, (на векторах которого построен симплекс), необходимо найти обратную матрицу:
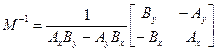 .
.
Умножение радиус-вектора искомой точки на матрицу 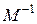 дает точку, которую достаточно проверить на попадание во внутреннюю или внешнюю область единичного симплекса, как было указано выше.
дает точку, которую достаточно проверить на попадание во внутреннюю или внешнюю область единичного симплекса, как было указано выше.
Идея четвертого метода, без строгого математического доказательства, была предложена одним из моих студентов Д. Трагером в 2005 году. Этот метод немного похож на метод углов приведенный в [8] и превосходит по скорости выполнения все из выше упомянутых методов. После описания для него будет приведен текст процедуры на Delphi, написанный автором данной работы.
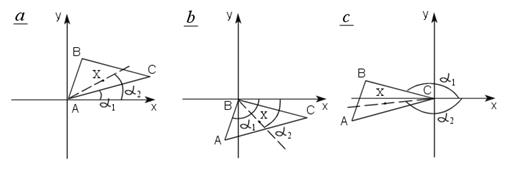 Рисунок 14. Последовательное измерение углов для получения разности
Рисунок 14. Последовательное измерение углов для получения разности 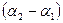 . .
|
Зададим порядок обхода вершин и перенесем вершины треугольника и проверяемую точку так чтобы начало координат совпало с точкой A, например, как показано на рис. 14 а. Конкретное направление обхода вершин треугольника, по или против часовой стрелки, не имеет значения. Рассмотрим углы 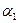 и
и 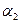 , как показано на Рис. 14 a, b и c, где X – точка, проверяемая на принадлежность внутренней области треугольника.
, как показано на Рис. 14 a, b и c, где X – точка, проверяемая на принадлежность внутренней области треугольника.
Утверждается, что только в том случае когда точка X находится внутри треугольника, знак 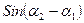 будет всегда совпадать для всех циклически выбираемых пар углов
будет всегда совпадать для всех циклически выбираемых пар углов 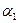 и
и 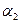 при последовательном совмещении вершин треугольника с началом координат. Пусть вершинам треугольника A, B, C и проверяемой точке X соответствуют радиус-векторы
при последовательном совмещении вершин треугольника с началом координат. Пусть вершинам треугольника A, B, C и проверяемой точке X соответствуют радиус-векторы 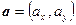 ,
, 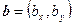 ,
, 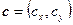 и
и 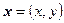 .
.
Найдем выражение, по которому можно легко вычислить знак 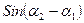 .
.
Для ситуации, изображенной на Рис.14 a
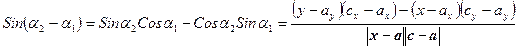
Очевидно, что знак 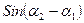 совпадает со знаком числителя правой части. Таким образом, получаем, что знак левой части определяется выражением
совпадает со знаком числителя правой части. Таким образом, получаем, что знак левой части определяется выражением
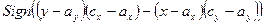 ,
,
где Sign – функция получения знака числа. Аналогичные рассуждения для оставшихся двух случаев, изображенных на рисунках b и с, приводят, соответственно, к выражениям
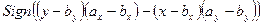
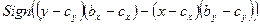 .
.
Доказательство правильности утверждения данного метода можно получить, если заметить, что знак 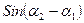 не меняется при повороте плоскости относительно начала координат. Тогда, для каждого из трех случаев, изображенных на рисунках 14 a, b и c, соответствующими поворотами плоскости можно добиться того, чтобы угол
не меняется при повороте плоскости относительно начала координат. Тогда, для каждого из трех случаев, изображенных на рисунках 14 a, b и c, соответствующими поворотами плоскости можно добиться того, чтобы угол 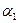 был равен нулю, а оставшаяся часть треугольника, вместе с проверяемой точкой, оказалась бы выше или ниже оси ox, в зависимости от выбранного направления обхода вершин треугольника.
был равен нулю, а оставшаяся часть треугольника, вместе с проверяемой точкой, оказалась бы выше или ниже оси ox, в зависимости от выбранного направления обхода вершин треугольника.
Рассмотрим версию функции InTri, в которой реализуется данный метод для целочисленных координат треугольника A =(AX,AY), B =(BX,BY), C =(CX,CY) и проверяемой точки X =(x,y). Функция выдает результат TRUE, если точка находится внутри или на границе треугольника (граница, таким образом, считается принадлежащей внутренней области треугольника), или FALSE, если точка находится за его пределами. Этой функцией удобно пользоваться если точки находятся на растровой сетке монитора, где координаты являются целыми числами.
function InTriI(x,y,AX,AY,BX,BY,CX,CY: Integer): boolean;
var
Res1,Res2: Integer;
begin
Res1:= (y-ay)*(cx-ax)-(x-ax)*(cy-ay);
Res2:= (y-cy)*(bx-cx)-(x-cx)*(by-cy);
// if (Res1>0)and(Res2<0)or(Res1<0)and(Res2>0) then
if Res1 XOR Res2 < 0 then
Result:= false //дальше не вычисляем
else
begin
Res2:= (y-by)*(ax-bx)-(x-bx)*(ay-by);
// if (Res1>0)and(Res2<0)or(Res1<0)and(Res2>0) then
if Res1 XOR Res2 < 0 then
Result:= false
else
Result:= true;
end;
end;
Обратите внимание на пару строк, которые дважды встречаются в тексте функции.
// if (Res1>0)and(Res2<0)or(Res1<0)and(Res2>0) then
if Res1 XOR Res2 < 0 then
Первая из двух строк специально закомментирована, так как вторая представляет собой ее оптимизированный вариант. Изначально в методе требуются действия, записанные в первой строке, где производится проверка на совпадение или несовпадение знаков вычисленных углов, что определяется переменными Res1 и Res2. Поскольку знак целого числа определяется его левым битом, точнее число считается отрицательным, если самый старший его бит равен 1, то он всегда будет равен единице при умножении двух чисел разного знака. Операцией целочисленного умножения здесь можно было бы воспользоваться, если бы операция XOR не давала аналогичный результат значительно быстрее. Код ассемблера, который генерирует Delpi, в случае использования операции XOR, примерно в 4 раза короче чем тот, что получается при использовании первой из двух рассмотренных нами строк на Паскале. Точнее, при включенной опции оптимизации компиляции в Delphi, вторая строка реализуется всего двумя инструкциями ассемблера, включая команду условного перехода. Но самое интересное, что аналогичный программный трюк можно применить и для вещественных входных параметров функции – типов Single и Double. Я не буду более вдаваться в технические тонкости, просто посмотрите текст функций. В случае вещественных входных параметров в них появляются небольшие отличия от целочисленного варианта.
Версия функции InTri для входных параметров типа Single.
function InTriS(x,y,AX,AY,BX,BY,CX,CY: Single): boolean;
var
Res1,Res2: Single;
ReI1: Integer absolute Res1;
ReI2: Integer absolute Res2;
begin
Res1:= (y-ay)*(cx-ax)-(x-ax)*(cy-ay);
Res2:= (y-cy)*(bx-cx)-(x-cx)*(by-cy);
// if (Res1>0)and(Res2<0)or(Res1<0)and(Res2>0) then
if ReI1 XOR ReI2 < 0 then
Result:= false //дальше не вычисляем
else
begin
Res2:= (y-by)*(ax-bx)-(x-bx)*(ay-by);
// if (Res1>0)and(Res2<0)or(Res1<0)and(Res2>0) then
if ReI1 XOR ReI2 < 0 then
Result:= false
else
Result:= true;
end;
end;//function InTriS
Версия функции InTri для входных параметров типа Double.
function InTriD(x,y,AX,AY,BX,BY,CX,CY: Double): boolean;
var
Res1,Res2: Double;
ReI1: Int64 absolute Res1;
ReI2: Int64 absolute Res2;
begin
Res1:= (y-ay)*(cx-ax)-(x-ax)*(cy-ay);
Res2:= (y-cy)*(bx-cx)-(x-cx)*(by-cy);
// if (Res1>0)and(Res2<0)or(Res1<0)and(Res2>0) then
if ReI1 XOR ReI2 < 0 then
Result:= false //дальше не вычисляем
else
begin
Res2:= (y-by)*(ax-bx)-(x-bx)*(ay-by);
// if (Res1>0)and(Res2<0)or(Res1<0)and(Res2>0) then
if ReI1 XOR ReI2 < 0 then
Result:= false
else
Result:= true;
end;
end;//function InTriD
В результате, как можно видеть по тексту приведенных процедур, задача решается в худшем случае за 6 операций умножения и 15 операций вычитания, а в лучшем случае всего за 4 операции умножения и 10 операций вычитания.






