ЭЛЕКТРОНИКА
Методические указания
к лабораторным работам
Санкт-Петербург
Издательство СПбГЭТУ «ЛЭТИ»
УДК 621.396
Электроника: Методические указания к лабораторным работам / сост.: В. А. Виноградов, А. А. Погодин. СПб.: Изд-во «ЛЭТИ», 2012. 68 с.
Содержат описания лабораторных работ, предназначенных для закрепления теоретических сведений, полученных при изучении аналоговых схем на операционных усилителях и транзисторах.
Предназначены для подготовки бакалавров по направлениям 140400 «Электроэнергетика и электротехника» и 220400 «Управление в технических системах», изучающих курс «Электроника».
Утверждено
редакционно-издательским советом университета
в качестве методических указаний
© СПбГЭТУ «ЛЭТИ», 2012
МЕТОДИКА ИЗМЕРЕНИЯ ОСНОВНЫХ ХАРАКТЕРИСТИК
ЭЛЕКТРОННЫХ ЦЕПЕЙ
В процессе выполнения лабораторных работ по дисциплине «Электроника» студенты измеряют основные параметры и характеристики электрон-ных цепей (схем). Несмотря на существенные различия в построении и назначении схем, наборы измеряемых параметров для этих цепей отличаются незначительно. В данном разделе приведены методики измерения тех параметров и характеристик, которые необходимо измерять при выполнении нескольких лабораторных работ.
1. Амплитудная характеристика (АХ) – зависимость напряжения на выходе (U выx) схемы от напряжения на ее входе (U вx). АХ измеряют на одной частоте, поэтому на вход цепи подают гармонический сигнал (частотой f), как правило, лежащей в полосе пропускания (усиления) схемы. Методику измерения АХ поясняет рис. М-1: источником сигнала является генератор (Г); поскольку часто генератор не содержит измерительного прибора, позволяющего точно контролировать уровень напряжения на его выходных клеммах, то к этим клеммам подключают вольтметр В1.
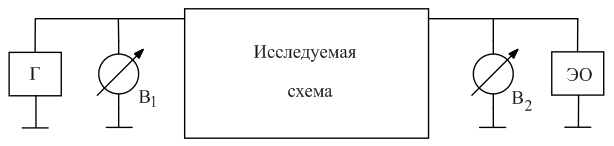Рис. М-1
|
С точки зрения исследуемой схемы выходное напряжение генератора, измеряемое вольтметром В1, является входным (U вx). К выходу схемы подключают вольтметр В2, регистрирующий U выx, а также электронный осциллограф (ЭО). Назначение осциллографа – демонстрировать форму сигнала на выходе схемы: нарушение линейной зависимости АХ сопровождается появлением нелинейных искажений выходного сигнала, т. е. отклонением его от гармонической формы. В процессе измерений необходимо изменять U вx при поддержании постоянства f.
2. Амплитудно-частотная характеристика (АЧХ) KU = KU (f), где KU = = | U выx/ U вx| – коэффициент передачи схемы по напряжению.Для измере-ния АЧХ применяют ту же схему рис. М-1, которая используется для измерения АХ.
Однако теперь фиксируют U вx (на уровне, при котором в выходном сигнале отсутствуют нелинейные искажения), а частоту изменяют. В процессе измерений удается зарегистрировать не коэффициент передачи, а лишь U выx, поэтому в дальнейшем следует обработать полученные данные. При построении графика АЧХ рекомендуется для большей наглядности частоту откладывать по оси абсцисс в логарифмическом масштабе: при этом любому десятикратному увеличению f соответствует отрезок фиксированной длины. Например, расстояние между отметками 10 и 100 Гц на оси выбрано равным одному сантиметру; между отметками 100 Гц и 1 кГц следует также отложить 1 см, между 1 и 10 кГц такой же отрезок и так далее.
3. Фазочастотная характеристика (ФЧХ) Df = Df(f), где Df – сдвиг фаз, который приобретает гармонический сигнал при прохождении через схему. Наиболее распространенный метод измерения ФЧХ – с использованием осциллографа, на экране которого получают фигуру Лиссажу. Методику измерений поясняет рис. М-2.
Рис. М-2
|
Сигнал с выхода схемы как правило подают на вход Υ осциллографа, а входной – на вход Х. Поскольку сигналы имеют различные амплитуды, то надо обеспечить равенство их графических изображений («вписать фигуру Лиссажу в квадрат»). Регулировать размер изображения сигнала можно только по входу Υ. После получения на экране фигуры, имеющей в общем виде форму эллипса, необходимо измерить ее размеры и рассчитать сдвиг фаз по формуле, приведенной на рис. М-3. Поскольку амплитуда выходного сигнала может меняться в зависимости от частоты, необходимо при переходе от одного значения f к другому заново обеспечивать равенство горизонтального и вертикального размеров фигуры Лиссажу – в противном случае при измерении фазы будет иметь место ошибка.
4. Входное сопротивление (R вx) схемы – отношение входного напряжения к входному току. Методику измерений поясняет рис. М-4.
Между генератором и входом исследуемой схемы включают магазин сопротивлений (МС). Применяемые в учебной лаборатории МС обеспечивают удовлетворительную точность измерений при
частотах сигнала не более 3 кГц. Первона- Рис. М-4
чально устанавливают нулевое сопротивление магазина (R м) и при этом фиксируют напряжение на вольтметре (оно равно напряжению на выходе генератора). Затем сопротивление магазина плавно увеличивают до тех пор, пока напряжение не снизится вдвое. Это означает, что магазин и входное сопротивление образовали делитель из двух равных сопротивлений, т. е. входное сопротивление схемы равно сопротивлению магазина.
5. Выходное сопротивление схемы (R выx) – отношение выходного напряжения к выходному току. Методику измерений поясняет рис. М-5.
 Рис. М-5
|
В начале измерений устанавливают максимально возможное сопротивление магазина, при этом магазин и вольтметр В2 соединяют параллельно и фиксируют показания вольтметра. Постепенно уменьшая сопротивление магазина, добиваются снижения напряжения, регистрируемого вольтметром, вдвое: при этом R м равно R выx исследуемой схемы.
Внимание! Подключение магазина с малым сопротивлением может привести к выходу из строя как макета, так и магазина сопротивлений.
Лабораторная работа № 1
ИССЛЕДОВАНИЕ ДИФФЕРЕНЦИРУЮЩИХ
И ИНТЕГРИРУЮЩИХ ЦЕПЕЙ
Целью работы является практическое ознакомление с пассивными и активными дифференцирующими и интегрирующими цепями – как со схемами, преобразующими форму импульсных сигналов, так и как с фильтрами.
Основные положения. Схема пассивной дифференцирующей цепи (ДЦ) приведена на рис. 1.1. Если на вход ДЦ подать видеоимпульс прямоугольной формы, например, положительной полярности (амплитудой U 0 и длительностью τи), то конденсатор будет заряжаться, заряд тока пойдет через резистор R, создавая на нем падение напряжения UR. Поскольку R включено параллельно выходным зажимам, то падение напряжения UR является одновременно выходным сигналом ДЦ (U выx). Напряжение UC возрастает по экспоненциальному закону, при этом принято считать, что заряд завершается за время, равное 3τ, где τ = RC – постоянная времени цепи. В первый момент значение выходного сигнала равно U 0, так как конденсатор еще не успевает зарядиться и все напряжение приложено к сопротивлению.
После окончания входного импульса (начиная с момента τи) конденсатор разряжается. Ток разряда (большой вначале) постепенно убывает. Поскольку разрядный ток течет в противоположном направлении (по сравнению с зарядным), то он создает на R, а значит на выходе схемы, так называемый обратный выброс – импульс полярности, противоположной знаку входного сигнала. Обратный выброс представляет опасность для некоторых видов нагрузки, и тогда его устраняют с помощью диодного ограничителя.
Процессы в ДЦ иллюстрируют диаграммы напряжений (рис. 1.2).
Возможны два варианта:
1) конденсатор успевает полностью зарядиться до окончания входного импульса, т. е. 3τ < τи; в этом случае выходной сигнал представляет собой пару коротких импульсов, сдвинутых друг относительно друга, имеющих одинаковые амплитуды и противоположную полярность (рис. 1.2, а);
2) конденсатор не успевает полностью зарядиться (3τ > τи), поэтому разряд начинается не с − U 0, а с уровня − UC m, инверсного достигнутому при заряде; обратный выброс имеет амплитуду − UC m меньшую, чем входной сигнал (рис. 1.2, б).
а б
Рис. 1.2
Из этих вариантов процедуре дифференцирования соответствует только первый, так как в этом случае преобразование формы сигнала цепью похоже на математический результат получения производной. Степень соответствия выходного сигнала ДЦ идеальному дифференцированию оценивают с помощью параметра, называемого ошибкой (погрешностью, %) дифференцирования: εд = (3τ /τи) ∙100.
Пассивная ДЦ при подаче на ее вход гармонического сигнала выполняет функции, отличные от преобразования формы сигнала. Емкости C соответствуетсопротивление XC = 1/(2π fC), убывающее с ростом частоты. R и XC образуютделитель из двух сопротивлений, коэффициент деления которого имеет вид R /(R − jXC). Коэффициент деления делителя совпадает с коэффициентом передачи схемы КU.. При f = 0 XC → ∞, поэтому коэффициент передачи дачи делителя равен 0, иначе говоря, сигнал со входа схемы на ее выход не проходит. При f → ∞ XC = 0, конденсатор пропускает сигнал со входа на выход без потерь и КU = 1. ДЦ является фильтром высоких частот.
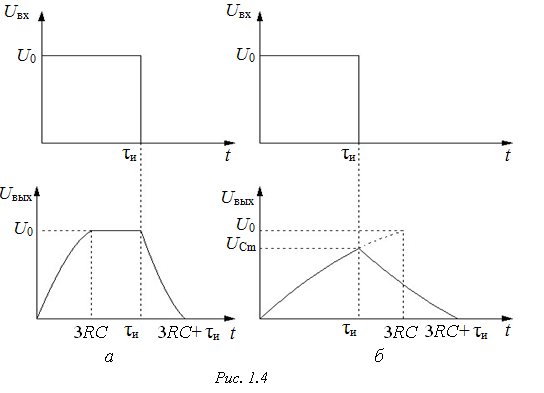
Интегрирование в математическом плане является операцией, обратной дифференцированию. Реализующая функцию интегрирования пассивная цепь (интегрирующая цепь (ИЦ), рис. 1.3) очень похожа на ДЦ, однако элементы R и C в схемах ДЦ и ИЦ переставлены местами. В ИЦ U выx = UC. При подаче на вход ИЦ видеоимпульса прямоугольной формы положительной полярности, имеющего амплитуду U 0 и длительность τи, конденсатор будет заряжаться, зарядный ток потечет через сопротивление R. После окончания входного импульса (начиная с момента τи) конденсатор разряжается. Таким образом, процессы в пассивных ДЦ и ИЦ полностью совпадают. Различие заключается лишь в том, на каком элементе схемы напряжение является выходным. Преобразование импульсов интегрирующей цепью иллюстрируют диаграммы напряжений рис. 1.4 (а – случай τи > 3 RC; б – τи < 3 RC).
Для обеспечения высокого качества интегрирования необходимо заряжать конденсатор как можно медленнее, так как только начальный участок экспоненты близок к линейной функции (интегралом от постоянной величины является линейная функция).
Ошибка интегрирования [%] определяется как εи = (τи/3τ) ∙100. Эта формула является обратной по отношению к выражению для εд. К сожалению, улучшение качества интегрирования в пассивной ИЦ сопровождается снижением амплитуды U выx, и при очень малых εи сигнал может быть утрачен.
Пассивная ИЦ при подаче на ее вход гармонического сигнала выполняет функции фильтра низких частот(ФНЧ). Как и в ДЦ, резистор R и XC образуютделитель из двух сопротивлений, но в ИЦ коэффициент деления равен (− jXC)/(R − jXC). При f = 0 XC → ∞, поэтому коэффициент передачи делителя равен 1, при f → ∞ XC = 0, конденсатор шунтирует выход схемы и КU = 0.
Схемы активных дифференцирующей и интегрирующей цепей на базе операционного усилителя приведены, соответственно, на рис. 1.5, а и б. В общем виде передаточная характеристика таких цепей в диапазоне рабочих частот ОУ может быть описана соотношением
K (jf) = − Z о.с(jf)/ Z вх(jf),
где Z о.с и Z вх – комплексные сопротивления цепи обратной связи и входной цепи соответственно. Формула является приближенной, так как не учитывает тот факт, что коэффициент усиления ОУ имеет хотя и огромное, но все же конечное значение.
| 
|
| а | б |
| Рис. 1.5 |
В цепи на рис. 1.5, а Z о.с(jf) = R, а Z вх(jf) = 1/ j 2π fС, т. е. K (jf) = j 2π fСR, цепь является фильтром высоких частот, а с точки зрения преобразования формы сигнала – дифференцирующей. Аналогично, цепь рис. 1.5, б имеет передаточную характеристику K (jf) = 1/ j 2π fСR, т.е. является фильтром низких частот, а значит, интегрирующей цепью. Достоинствами активных дифференцирующих и интегрирующих цепей по сравнению с пассивными являются большая точность выполнения соответствующих математических функций, а также возможность одновременно усиливать сигнал и преобразовывать его форму.
Описание лабораторной установки. В состав лабораторной установки входят лабораторный макет, генератор (формирующий гармонические сигналы, а также последовательности прямоугольных импульсов типа меандра), два вольтметра переменного напряжения и осциллограф. Галетный переключатель позволяет поочередно исследовать различные дифференцирующие и интегрирующие цепи; параметры цепей можно изменять с помощью коммутаций элементов R и С на лицевой панели макета.
Порядок выполнения работы:
1. Подать напряжения питания +15 и –15 В на макет.
2. Исследовать пассивные и активные дифференцирующие и интегрирующие цепи как фильтры:
а) измерить амплитудно-частотные характеристики цепей в диапазоне частот (f)10 Гц…1 МГц. Параметры цепей (значения R и С) устанавливать по указанию преподавателя;
б) определить граничные частоты (f гр) исследованных цепей, исходя из условия K (f гр) ≈ 0,7 [max K (f)].
3. Исследовать пассивные и активные дифференцирующие и интегри-рующие цепи как преобразователи формы импульсов:
а) для этого подать с генератора на входы различных цепей сигналы в виде меандра с различной длительностью импульсов (τи), зарисовать с экрана осциллографа или сфотографировать форму сигналов на выходах цепей;
б) определить ошибки дифференцирования и интегрирования (εд и εи).
Содержание отчета:
1. Схемы соединения приборов при измерениях.
2. Схемы исследованных дифференцирующих и интегрирующих цепей.
3. Результаты измерений и расчетов по п. п. 2,3 (графики АЧХ, значения f гр, форма выходных сигналов с указанием τи, значения εд и εи).
4. Выводы.
Лабораторная работа № 2
