При независимых переменных T,v характеристич функцией явл-ся разность F=u-Ts, введенная в т/д-ку Гельмгольцем и названная им свободной энергией. Дифференциал этой ф-ии имеет вид dF=-sdT-pdv. Дифференциал функциональной зависимости F=f(T,v),имеющий вид dF=(δF/δT)νdT+(δF/δν)Tdv, включает частные производные (δF/δT)ν==-s; (δF/δν)T=-p. Сл-но, своб Е явл-ся характеристической функцией при независимых переменных T и ν. По аналогии со свободной Е Дж. Гиббс ввел в т/д-у свободную энтальпию G=h-Ts=u+pv-Ts, называемую иногда т/д-ким потенциалом Гиббса. Дифференциал свободной энтальпии имеет вид dG=-sdT+vdp. Частные производные свободной энтальпии определяют соответсвующие т/д-ские параметры в виде (δG/δT)p=-s; (δG/δp)T=ν; свободная энтальпия явл-ся характеристической функцией при независимых переменных T и p.
23. При взаимодействии какого-л рода в сист одновременно изм-ся значения нескольких параметров состояния.Параметры состояния, обязательно изменяющиеся при наличии вд-ия данного рода и не изменяющиеся под влиянием взаимодействия иных родов, называются коорд тд-го состояния. Cуществует функц состояния, изменение кот (в равновесных процессах) однозначно связано с количеством Е, передаваемым в форме теплоты. Эта функция состояния была названа Клаузиусом энтропией. Энтропия явл-ся параметром состояния, выполняющим роль координаты термического состояния тд-ой системы. Другую важную для тд-го анализа группу величин, характеризующих состояние сист, составляют так называемые потенциалы тд-х вд-ий.
Потенц вд-я некот рода наз параметр состояния, различие значений кот между сист и окр ср на контрол пов-ти приводит к возникновению вд-ия данного рода, т.е. к передаче Е в данной форме м\у сист и окр ср. Потенциалами термодеформационной тд-ой сист явл-ся: для теплового вд-ия - термодинамическая т-ра, для деформационного механич вд-ия – давление.
25. Изменение полной Е системы
dE=(ul + p1 v1 + wl2/2 + gy1) dm1- (u2 + p2 v2 + w22/2 + gy2) dm2 + dQ - dLT - dL, (2.34)
где v1 = dV1/dm1,и v2=dV2/dm2 – уд объемы рабочего тела во входном и выходном сечениях.
Уравнение. (2.34) применимо как для стационарных, так и для нестационарных процессов, происходящих в сист
. Процесс будет нестационарн, если поступление Е или массы раб тела за кажд промежуток врем не будет равно расходу Е и массы. В этом случ скорость изменения Е системы выразится как 
, (2.35)
где m1, m2- массовые расходы раб тела на входе и выходе, кг/с;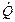 
- поток подводимой теплоты, Дж/с; 
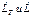- мощности, отводимые от системы, Дж/с.
В стационарном пр-се поступление массы раб тела и Е в сист равно их расходу, а объем системы постоянен:dE=0; dm1=dm2=dm; dV=0.
При этих условиях деление всех членов уравнения (2.34) на dm дает уд объемы v1 = dV1/dm и v2= dV2/dmи удельные количества q= dQ/dmи lт= dLT/dm, отнесенные к 1 кг рабочего тела, прошедшего через систему [1]. С учетом полученных соотношений ур (2.34) получит вид (u2+p2v2) - (u1 +p1v1) = q - lт - (w22 /2-w12/2) -g(y2-y1).2.36
В уравнениях баланса Е раб тела в проточной системе (2.35), (2.36) обязательно присутствует сумма внутренней Е рабочего тела и работы ввода или вывода. Эта сумма выражена ч\з параметры состояния и сама, т о, является функцией состояния. Функц состояния, равная сумме внутренней Е и произведения давления на объем рабочего тела, называется энтальпией h: h=u+pv. Сл-но Ур 1 зак тд-ки для конечного изменения состояния рабочего тела в проточной тд-ой сист мож представить в видеDh = q -lт - D(w2/2) -D(gy). в этом уравнении: Dh=h2-h1- изменение уд энтальпии; D (w2/2) = w22/2-w12- изменение уд кинетич Е; D(gy) =gy2-gy1– измен уд потенциаль Е рабочего тела.
