Прямая перпендикулярная плоскости, если ее горизонтальная проекция перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция перпендикулярна фронтальной проекции фронтали плоскости (см. таблицу 14).
Таблица 14 – Перпендикулярность прямой и плоскости
| Прямая и плоскость занимают общее положение | Прямая и плоскость занимают частное положение | ||
| Плоскость задана линиями уровня | Линии уровня строятся в плоскости | ||

| 
| 
| 
|
| Точка А является основанием перпендикуляра b | Основание перпендикуляра на чертеже отсутствует. | Точка N – основание перпендикуляра, определяется по принадлежности точки прямой |
Перпендикулярность двух плоскостей
Две плоскости взаимно перпендикулярны, если в любой из них можно построить прямую, перпендикулярную другой плоскости.
Примеры перпендикулярных плоскостей приведены в таблице 15
Таблица15 – Перпендикулярность двух плоскостей
| Обе плоскости занимают общее положение | Одна из плоскостей занимает частное положение | |
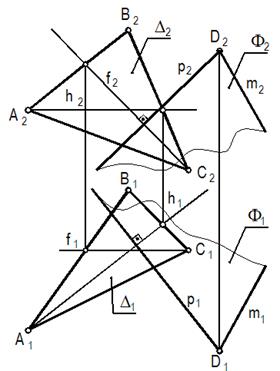
| 
| |
| Обе плоскости занимают частное положение | ||

| 
| |
Решение задач по варианту В
Задача 1
Построить проекции плоскости, параллельной плоскости, заданной треугольником АВС, и отстоящей от неё на 30 мм.
При решении данной задачи для определения метрической характеристики – расстояние между двумя параллельными плоскостями, используется правило прямоугольного треугольника: истинная величина отрезка прямой общего положения равна гипотенузе прямоугольного треугольника, у которого один катет равен проекции отрезка (катет-проекция А1В1), а другой — разности координат концов отрезка, определяющих удаление от плоскости проекций P1 (см. рисунок 8).

Рисунок 8
Последовательность решения задачи представлена в таблице 16.
Таблица 16 – Последовательность решения задачи 1
| 1) По исходным данным построить плоскость треугольника АВС. В плоскости провести фронталь f(f1,f2) и горизонталь h(h1,h2) | 2) Из вершины А восставить перпендикуляр АЕ к плоскости, заданной треугольником АВС – А2Е2^f2; А1Е1^h1. Точку Е на перпендикуляре выбрать произвольно |

| 
|
| 3) С помощью правила прямоугольного треугольника определить истинную величину отрезка ЕА. На нём отложить от точки А заданное расстояние – 30 мм, измеряемое отрезком АМ. | 4) Построить проекции М1 и М2 точки М. Через точку М провести искомую плоскость, исходя из условия параллельности двух плоскостей (см. таблицу 9). |

| 
|
Задача 2






