Вивчення принципу роботи ОКГ(лазера)

Курс

 

 

МЕТОДИЧНІ ВКАЗІВКИ ТА ІНСТРУКЦІЇ ДО ЛАБОРАТОРНИХ РОБІТ З ФІЗИКИ

Можна використовувати для студентів 2 курсу.

Запоріжжя: ЗАК, 2006.- 32c.

 

Укладач: О.В.Чепурна, викладач 1 категорії

 

 

Затверджено на засіданні

ПЦК фізико-математичних дисциплін

Протокол № 7 від 1.03. 2006 року

 

 

 

 

Міністерство освіти і науки україни

Запорізький авіаційний коледж

Ім. О.Г.Івченка

 

ЗАТВЕРДЖУЮ

Заступник директора з НВР

В.І.Сніжко

 

 

МЕТОДИЧНІ ВКАЗІВКИ ТА ІНСТРУКЦІЇ ДО ЛАБОРАТОРНИХ РОБІТ З

Курс

 

спеціальність 5.090227

 

Зміст

 

1. Визначення об`єму та маси геометричних тіл................5
2. Спостереження процесів плавлення та кристалізації гіпосульфіта.......................................................................7
3. Визначення коефіцієнту поверхневого натягу методом відриву кільця..................................................................................10
4. Визначення періоду дифракційної решітки............13
5. Вивчення принципу роботи ОКГ(лазера)........................17

Додаток А..............................................................................23

 

 

Лабораторна робота №1

Визначення об`єму та маси геометричних тіл

Мета

За допомогою вимірів штангенциркулем визначити об`єм тіл,та розрахувати густину.

 

2 Завдання:

2.1 Виміряти масу деталей за допомогою терезів.

2.2 Обчислити об’єм тіл.

2.3 Розрахувати густину тіл.

2.4 За розрахованою густиною користуючись довідником№1 визначити матеріал, з якого виготовлені тіла.

3 Обладнання:

3.1 Штангенциркуль.

3.2 Набір тіл різної геометричної форми.

3.3.Терези.

 

4 Теоретичні положення

За допомогою штангенциркуля можна виміряти довжину, зовнішній і внутрішній діаметр трубок, глибину отвору.

Знаючи ці розміри можна розрахувати об`єм

геометричних тіл.

Ноніусом називають доповнення до звичайного масштабу,яке дозволяє збільшити точність вимірів з наданим масштабом в 10-20 разів.

Лінійний ноніус уявляє собою невелику лінійку,яка ковзає вздовж основного масштабу. На лінійці нанесено маленьку шкалу, яка складається з мм ділень.

Одним із приладів, у яких використовується ноніус є штангенциркуль.

Порядок виконання роботи

5.1 5а допомогою штангенциркуля виміряти кожен, необхідний для обчислення об`єму параметр тіла.

Провести аналогічні виміри для тіла іншої геометричної форми.

Визначити для кожного тіла за допомогою терезів масу.

Розрахувати для кожного тіла об`єм використовуючи формулами геометрії

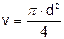( h)

Визначити густину речовини із якої виготовлено тіла за формулою

5.6 Дані занести до таблиці:

№ п/п

м

в м

с м

D м

H м

V

m кг

речовина

5 .7. Знайти у довіднику близьку за значенням до обчисленої густину і визначити матеріал з якого виготовлено тіла

 

6 Контрольні питання.

6.1 Для виконання лабораторної роботи навчитися вимірювати (і робити відлік) за допомогою штангенциркуля.

6.2 Дати фізичний зміст поняття “густина”.

6.3 Вміти перекладати у систему СІ: 1 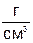; 1 ; 1 .

7 Висновок: зробити самостійно.

8Домашнє завдання

підготуватись до наступної лабораторної роботи.

 

 

ЛАБОРАТОРНАЯ РАБОТА № 2

Спостереження процесів плавлення та кристалізації гіпосульфіта.

МЕТА

Дослідити процеси плавлення та кристалізації.

ЗАВДАННЯ

2.1 За даними досліду побудувати на міліметровому папері графік плавлення та кристалізації гіпосульфіту.

2.2 За графіком визначити температуру плавлення гіпосульфіту (та кристалізації)

 

ОБЛАДНАННЯ

 

3.1Колба з гіпосульфітом.

3.2Посудина з водою.

3.3Лабораторна плитка.

3.4Термометр.

3.5Секундомір.

 

4 Вказівки на теоретичний матеріал

4.1 Фазові переходи 1 і 2 роду. (Л.1.,с.141)

4.2 Плавлення та кристалізація. (Л.1.,с139)

 

5 Теоретичні положення.

 

Графік, побудований у координатах „ температура – час”, відображує процеси, які відбуваються під час досліду при нагріванні і охолодженні з кристалізацією. Спочатку температура зростає пропорційно часу. Нахил прямої до осі абсцис залежить від потужності нагрівача. Під час плавлення температура речовини не змінюється, уся теплота іде на руйнування зв’язків у кришталевій решітці і збільшення кінетичної енергії молекул. Теоретично на цій ділянці графік уявляє собою пряму АВ, яка паралельна осі абсцис (рис 1). Але у зв’язку з тим, що температура у різних містах колби з гіпосульфітом внаслідок неідеальної теплопровідності неоднакова, а термометр вимірює температуру шару навколо головки, то у дійсності процес протікає по кривій.

Після того як температура гіпосульфіту піднялась приблизно до 50...60 C, колбу починають охолоджувати у холодній воді по можливості до більш низької температурі (лінія С1D). Якщо охолодження проводити достатньо швидко і без дотиків, розплав можна довести до переохолодженого стану.

Переохолоджений гіпосульфіт кристалізується з виділенням теплоти кристалізації при стряхуванні або попаданні у нього стороннього тіла і особливо при внесенні у розплав кристалика твердого тіла (центрів кристалізації). Теплота, яка при цьому виділяється, нагріває гіпосульфіт.

Якщо при кристалізації не охолоджувати колбу з гіпосульфітом, то температура може піднятися до точки плавлення (лінія DE), або процес кристалізації може відбуватися при більш низькій температурі.

 

рисунок 1

 

6 ХІД РОБОТИ

6.1 Нагріваємо колбу з гіпосульфітом у водяній бані.

6.2 Як тільки температура почне підійматись, вмикаємо секундомір і записуємо значення температури через кожні 10-15 секунд.

6.3 При досягненні температури 50-60 С вимкнути плитку і опустити колбу з гіпосульфітом у холодну ванну. Продовжуємо спостерігати за зменшенням температури, записуючи значення через кожні 10-15 секунд.

6.4 Коли охолодження припиниться, убирають воду і у розплав вводять кристалики гіпосульфіта. При цьому продовжують записувати значення температур до того моменту, поки температура після підвищення не почне падати.

6.5Отримані результати занести до таблиці:

 

Час,с
t,С

6.6 Побудувати графік на міліметровому папері.

6.7 Визначити температуру плавлення гіпосульфіту та кристалізації.

 

7 КОНТРОЛЬНІ ПИТАННЯ

7.1Фізичний зміст понять: температура плавлення, теплота плавлення, кристалізація. Умови плавлення.

7.2Чому температура під час плавлення не змінюється?

7.3Дати пояснення за побудованим графіком змінення температури із зміненням часу.

 

8 Література

Трофимова Т.И. Курс физики: Учеб. пособие для вузов. 1999

9 ВИСНОВОК: зробити самостійно.

10 ДОМАШНЄ ЗАВДАННЯ: підготуватись до наступної лабораторної роботи

 

Лабораторна робота №3

Визначення коефіцієнту поверхневого натягу методом відриву кільця.

Мета.

Визначити коефіцієнт поверхневого натягу води та порівняти з теоретичним значенням.

 

Завдання

2.1 Методом відриву кільця визначити коефіцієнт поверхневого натягу води.

2.2 Необхідні виміри зробити за допомогою штангенциркуля.

2.3 Обчислити за експериментальними даними коефіцієнт поверхневого натягу води.

 

Обладнання

3.1Спеціальна установка.

3.2 Штангенциркуль.

3.3 Технічні ваги.

3.3 Досліджувана рідина – вода.

 

4 Вказівки на теоретичний матеріал

4.1 Властивості поверхні рідини. (Л.1., с.126)

4.2 Змочування. (Л.1., с.130)

 

5 Теоретичні положення

Поверхневий натяг можна визначити шляхом виміру сили, яку потрібно прикласти перпендикулярно до поверхні рідини для відриву різних твердих тіл від цієї поверхні. Так як тіло, яке відриваємо,змочується рідиною, то разом з ним підіймається деяка кількість рідини, т.б. вільна поверхня рідини буде збільшуватись. Внаслідок намагання цієї поверхні скоротитися з’являється сила поверхневого натягу. Якщо сила, яка діє на тіло, дорівнює за значенням силі поверхневого натягу, то тіло одірветься.

Роздивимось кільце із зовнішнім діаметром D товщею d, яке дотикається поверхні рідини. При підніманні кільця над поверхнею рідини між кільцем і поверхнею води утворюється викривлена плівка. Зовнішня поверхня цієї плівки тягне кільце вниз із силою:

F=σ ∙ π ∙ D

внутрішня поверхня— із силою:

F= σ ∙ π ∙ (D – d)

Рівнодіюча сила, яка утримує кільце:

σ π D + σ π (D – d) ≈ 2 σ ∙ π (D – d).

У момент відриву F = 2σ ∙ π (D – d), звідки

 

Так як діаметр і товща кільця можуть бути виміряні штангенциркулем, то визначення коефіцієнту поверхневого натягу зводиться до визначення сили відриву F.

 

Порядок виконання роботи

6.1 Воду налити у ємність і обережно підняти її до торкання рідини і кільця.

6.2 Помітити по шкалі покази рівню на якому знаходиться кільце.

6.3 Обережно опускаючи ємність з рідиною помітити покази рівню кільця по шкалі у момент відриву кільця (максимальне розтягнення пружини).

6.4 Загрузити площину гирьками, поки кільце не опуститься на раніше помічені покази. Користуючись законом Гука, знайти значення сили поверхневого натягу(у момент відриву кільця сила поверхневого натягу зрівноважена силою пружності; сила пружності буде чисельно дорівнювати силі тяжіння, значить сила натягу чисельно дорівнює модулю сили тяжіння)

F=mg,

де m-маса гирьок, якими ми загрузили кільце, g-прискорення вільного падіння.

6.5 За формулою (*) обчислити коефіцієнт поверхневого натягу води.

6.6 Дослід повторити 3 – 4 рази, результати занести до таблиці1.

 

Таблиця 1

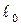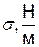
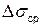
№	мм	, мм	F,Н						d, мм	D, мм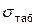

 

6.7 Обчислити абсолютну і відносну похибки.

6.8 Порівняйте розраховане значення поверхневого натягу води із табличним.

7 Контрольні питання

 

7.1 Фізична сутність понять: поверхневий натяг, змочування, сила поверхневого натягу, енергія поверхневого шару.

7.2 У яких одиницях вимірюється поверхневий натяг?

7.3 Лапласівський тиск. Меніск. Умова підняття рідини у капілярі.

 

8 Література

Трофимова Т.И. Курс физики: Учеб. пособие для вузов. 2004.-560 с.

 

Висновок

зробити самостійно.

10 Домашнє завдання: вивчити конспект лекцій з даної теми.

 

Лабораторна робота №4

Визначення періоду дифракційної решітки

МетА

Визначити період дифракційній решітки просторову частоту

Завдання

2.1 Роздивитись та налагодити пристрій.

2.2 Визначити tgθ за формулою: tg θ = b / a

2.3 Виконати роботу, та розрахувати період дифракційної решітки за формулою

 

d=m•λ / sin θ

2.4 Розрахувати просторову частоту за формулою N = 1 / d

2.5 Відповісти на контрольні питання.

Обладнання

 

3.1. Лазерний випромінювач з довжиною хвилі λ=635нм.

3.2 Дифракційна решітка.

3.3 Оптична mini- лава.

3.4 Екран.

4 Вказівки на теоретичний матеріал

4.1 Дифракція світла (Л2.с.335)

4.2 Дифракційна решітка.

Вимірювання довжини світлової хвилі (Л2.с.339)

5 Теоретичні положення

Дифракцією називається огинання хвилями перешкод, що зустрічаються на їх шляху, або у більш широкому розумінні будь яке відхилення розповсюдження хвиль поблизу перешкод від законів геометричної оптики. Завдяки дифракції хвилі можуть потрапляти у область геометричної тіні, огинати перешкоди, проникати через невеликі отвори в екранах і т. п.

Явище дифракції пояснюється за допомогою принципу Гюйгенса, згідно якого кожна точка, до якої доходить хвиля, є центром вторинних хвиль, а огинаюча цих хвиль дає положення хвильового фронту у наступний момент часу.

Явище дифракції характерно для хвильових процесів. Велике практичне значення має дифракція, що спостерігається при проходженні світла через одномірну дифракційну решітку - систему паралельних щілин рівної ширини, що лежать в одній площині і розділенні рівними завширшки непрозорі" • проміжками

Дифракційна картина на решітці визначається як результат взаємної інтерференції хвиль, що ідуть від усіх щілин, тобто в дифракційній решітці використовується багатопроменева інтерференція когерентних дифрагованних променів світла, що йдуть від усіх щілин.

Роздивимось дифракційну решітку (Рисунок 1).

Рисунок 1

 

M N C D

Д. Решітка

Лінза

Екран

 

Період дифракційної решітки:

 

d = a + b

де а, Ь - ширина прозорого і непрозорого проміжків. Так як щілини знаходяться одна від одної на однакових відстанях, то різниця хода променів, що йдуть від двох сусідніх щілин, будуть для даного напряму ф однакові в межах всієї дифракційної решітки:

Δ=CF=(a + b) sin φ = d sin φ

(5.1)

Отже, ті напрями, в яких ідуть промені, що створюють світлі смуги на екрані, характерні тим, що в різниці ходу променів від сусідніх щілин завжди вкладається m довжин хвиль, де m - ціле число. Отже, маємо формулу дифракційної решітки:

m λ = d. sin φ

 

Формула (5.1) справедлива і при m=0: проти центра решітки на екрані також буде світла смуга. Кожну з світлих ліній на екрані називають максимумом, а значення т, яке їй відповідає - його порядком. Отже, проти центру решітки видно найяскравіший максимум нульового порядку, з обох боків від нього на однакових відстанях видно менш яскраві максимуми першого порядку, потім менш яскраві максимуми другого порядку і т.д. Дослід показує, що всі ці максимуми розміщенні на однакових відстанях один від одного.

Розподіл випромінювання за частотами коливань (за довжинами хвиль) називають спектром цього випромінювання Спрямовуючи на решітку біле світло можна добути його спектр. Він складається з усіх кольорів радуги.

Дифракційну решітку можна використати для визначення складу світлового випромінювання, бо світло яке відповідає різним довжинам хвиль, дає максимум в різних місцях екрана.

Порядок виконання роботи

6.1 Ввести у промінь лазерного діода дифракційну решітку
перпендикулярно до осі проміння.

6.2 Встановити відбиваючий екран перпендикулярно до лазерного проміння.

6.3 Виміряти відстань "b" від "О'' порядку дифракції до m-го порядку, за.

допомогою вимірювальної шкали на екрані (дивись рисунок 2).

6.4 Виміряти відстань "a" від дифракційної решітки до екрана. 6.5 Розрахувати кут дифракції "θ" для m-го порядку tg θ=b/а. Порезультатах вимірювань розрахувати період дифракційної решітки заформулою 6.1.

d=m•λ/tgθ (6.1)

6.6 Розрахувати просторову частоту дифракційної решітки за формулою

 

N = /d (6.2), де =1 мм,d - період решітки.

6.7 Повторити дослід 3 рази.

6.8 Усі вимірювання та розрахунки занести до таблиці.

6.9 Порівняти отриманий результат з паспортними даними на дифракційну решітку.

 

Таблиця – Результати вимірювань та розрахунків:

 

№	Довжина хв.	Від- стань   a,м	Відстань в,м		Порядок макс.   m	Період d	N

7 Контрольні запитання

7.1 В чому полягає явище інтерференції та дифракції світла?

7.2 Як визначити найбільший порядок спектра дифракційної решітки?

7.3 Чому при використанні білого світла лише центральний максимум білий, а всі бокові райдужно офарбовані?

7.4 Розв’язати задачу: Визначити кількість штрихів на 1мм дифракційної решітки, якщо куту π/2 відповідає максимум п'ятого порядку для монохроматичного світла з довжиною хвилі 0,5мкм

7.5 Сформулювати закони відбивання і заломлення світла.

8 Література

8.1. Жданов Л.С. Жданов ГЛ. "Фізика"

8.2. Трофимова Т.И. Курс физики: Учеб. пособие для вузов. 2004.-560 с.

 

9 Висновок:

зробити самостійно.

10 Домашнє завдання: Л2, П182,с343.

 

Лабораторна робота №5

Вивчення принципу роботи ОКГ(лазера)

Мета

 

Вивчити принцип роботи ОКГ (лазера)

Обладнання

 

2.1 Лазер;

2.2 Дифракційна решітка;

2.3 Призма.

Завдання

 

3.1 Вивчити принцип дії ОКГ;

3.2 Спостерігати розклад монохроматичного світла дифракційною решіткою у спектр.

3.3 Спостерігати відхилення променю призмою.

 

4 Вказівки на теоретичний матеріал

4.1 Поглинання. Самовільне та вимушене випромінювання (Л.1.,с434)

4.2 Оптичні квантові генератори (Л1.,с436)

5 Теорія

Поглинені атоми можуть знаходитися лише у квантових станах із дискретними значеннями енергії Е₁, Е₂,....Е_n. Заради простоти розглянемо тільки два з цих станів (1 і 2) з енергіями Е₁ і Е₂. Якщо атом знаходиться в основному стані 1, то під дією зовнішнього випромінювання може здійснитися в змушений перехід стан 2 (рис. 1а), що призводить до поглинання. Ймовірність подібних переходів пропорційна щільності випромінювання, що викликає ці переходи.

Атом, який знаходиться у збудженому стані 2, може через деякий проміжок часу спонтанно, без яких-небудь зовнішніх впливів, перейти в стан із нижчою енергією (у нашому випадку в основне), віддаючи надлишкову енергію у вигляді електромагнітного випромінювання (випускати фотон з енергією = Е₂ - Е₁).

Процес випускання фотона збудженим атомом (збудженою мікросистемою) без зовнішніх впливів називається спонтанним (або довільним) випромінюванням (рис. 1б). Чим більше ймовірність спонтанних переходів, тим менше середній час життя атома в збудженому стані. Тому що спонтанні переходи взаємно не зв’язані, то спонтанне випромінювання некогерентне. Якщо на атом, що знаходиться у збудженому стані 2, діє зовнішнє випромінювання з частотою, що задовольняє умові

= Е₂ - Е₁ , то виникає змушений (індукований) перехід в основний стан 1 із випромінюванням фотона і тієї ж енергії = Е₂ - Е₁ (рис. 1в). При подібному переході відбувається випромінювання атомом фотона додаткового до того фотону, під дією якого відбувся перехід. Виникаюче в результаті таких переходів випромінювання називається змушеним (індукованим) випромінюванням.

 

Поглинання Спонтанне

Випромінювання

А) б)

Рис. 1

Змушене

випромінювання

 

 

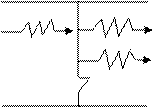
Рис.1 (в)

Таким чином, процес змушеного випромінювання залучені два фотона: первинний фотон, що викликає випускання випромінювання збудженим атомом і вторинний фотон, який випущено атомом. Істотно, що повторно фотони не відрізняються від первинних, приходячи точною їхньою копією. Змушене випромінювання строго когерентне з випромінюванням, що змушує.

Випущені фотони, рухаючись в одному напрямку і зустрічаючи інші збуджені атоми, стимулюють подальші індуковані переходи, і число фотонів росте лавиноподібно. Проте поряд із змушеним випромінюванням можливий і конкуруючий процес—поглинання. Тому для посилення падаючого випромінювання необхідно, щоб число актів змушеного випромінювання фотонів (воно пропорційно заселеності збуджених станів) перевищувало число актів поглинання фотонів (воно пропорційно заселеності основних станів). У системі атомів, яка знаходиться у термодинамічній рівновазі, поглинання падаючого випромінювання, буде переважати над вимушеним, тобто падаюче випромінювання при проходженні через речовину буде послаблюватися.

Щоб середовище посилювало падаюче на нього випромінювання, необхідно створити нерівновісний стан системи, при якому число атомів у збуджених станах було б більше, чим їхнє число в основному стані. Такі стани називаються станами з інверсією населеностей. Процес створення нерівновісного стану речовини (переклад системи в стан з інверсією населеностей) називається накачуванням. Накачування можна здійснити оптичними, електричними й іншими засобами.

 

Оптичний квантовий генератор:

Практично інверсний стан середовища здійснено в принципово нових джерелах випромінювання – оптичних квантових генераторах, або лазерах.

Найважливішими з існуючих типів лазерів є твердотільні, газові, напівпровідникові і рідинні (в основу такого розподілу призначений тип активного середовища).

Лазер обов’язково має три основних компоненти:

1) Активне середовище, у якому створюються стани з інверсією неселеностей;

2) Системи накачування (пристрій для створення інверсії в активному середовищі);

3) Оптичний резонатор (пристрій, що виділяє в простір виборчий напрям пучка фотонів і формуючий вихідний світловий пучок).

Першим твердотільним лазером (1960; США), що працює в видимій області спектра (довжина хвилі випромінювання 0,6943 мкм), був рубіновий лазер (Т. Мейман (р.1927)). У ньому інверсна населеність рівнів здійснюється по трьохрівневій схемі, запропонованій в 1955 р. Н. Г. Басовим і А. М. Прохоровим. Кристал рубіна являє собою окис алюмінію Al₂O₃, у кристалічній решітці якого деякі з атомів Al заміщені тривалентними іонами Cr³⁺¹ (0,03 і 0,05% іонів хрому відповідно для рожевого і червоного рубіна). Для оптичного накачування використовується імпульсна газорозрядна лампа. При інтенсивному опроміненні рубіна світлом потужної імпульсної лампи атоми хрому переходять із нижнього рівня 1 на рівні широкої смуги 3 (рис. 2). Тому що час життя атомів кульгає в збуджених станах мало (менше 10^-7 с), то здійснюються або спонтанні переходи 3-1 (вони незначні), або найбільше ймовірні безвипромінювальні переходи на рівень 2 (він називається метастабільним) із передачею надлишку енергії гратам кристалу рубіна. Перехід 2-1 заборонений правилами добору, тому тривалість збудженого стану 2 атомів хрому порядку 10^-3 с, тобто приблизно на чотири порядки більше, ніж для стана 3. Це веде до „накопичення” атомів хрому на рівні 2. При достатній потужності накачування їхня концентрація на рівні 2 буде набагато більше, ніж на рівні 1, тобто виникає середовище з інверсійною населеністю рівня 2.

Кожний фотон, що випадково народився при спонтанних переходах, може індицювати (породжувати) в активному середовищі багато змушених переходів 2-1, у результаті чого з’являється ціла лавина вторинних фотонів, що є копія первинних. Таким чином, породжується лазерна генерація. Проте спонтанні переходи носять випадковий характер, і фотони, що спонтанно народжуються, випускаються в різних напрямках. Тим самим у самих різних напрямках поширюється і лавини повторних фотонів. Отже, випромінювання, що складається з подібних лавин, не може мати високі когерентні властивості.

Для виділення напрямку лазерної генерації використовується принципово важливий елемент лазера - оптичний резонатор. У найпростішому випадку їм служить пара повернутих один до одного (або увігнутих) дзеркал на загальній оптичній осі, між якими міститься активне середовище (кристал або кювету з газом). Як правило, дзеркала виготовляються так, що від одного з них випромінювання цілком відбувається, а друге - полупрозоре. Фотони, що рухаються під кутами до осі кристала або кювети, виходять з активного середовища через її бічну поверхню. Ті ж із фотонів, що рухаються вздовж осі, багаторазово відіб’ються від протилежних торців, щораз викликаючи змушене випромінювання, і т.д. Тому що фотони, що виникли при змушеному випромінюванні, рухаються в тому ж напрямку, що і первинні, то потік фотонів, рівнобіжний осі кристала або кювети, буде лавиноподібно наростати. Багаторазово посилений потік фотонів виходить через напівпрозоре дзеркало, створюючи строго спрямований світловий промінь величезної яскравості. Таким чином, оптичний резонатор „з’ясовує” напрямок (уздовж осі), що посилюється фотонним потоком, формулюючи тим самим лазерне випромінювання з високими когерентними властивостями.

 

 

Рис. 2

 

Лазерне випромінювання має такі властивості:

1. тимчасове і просторова когерентність;

2. монохроматичність (Dl<10¹¹ м);

3. велика щільність потоку енергії;

4. дуже мала кутова розбіжність променя.

 

Наприклад, при використанні спеціального фокусування променя лазера, спрямований із Землі, дасть на поверхні Місяця світлову пляму діаметром приблизно 3 км (промінь прожектора освітив би поверхню діаметром приблизно 40000 км).

Ккд лазерів коливається у широких межах від 0,01% (для гелій-неонового лазера) до 75% (для лазера на склі з неодимом), хоча в більшості лазерів ккд складає0,1-1%. Створено потужний СО₂-лазер, що генерує інфрачервоне випромінювання (l=10,6 мкм), ккд якого (30%) перевищує ккд існуючих лазерів, що працюють при кімнатній температурі.

Застосування лазерів для опрацювання, різання і мікрозварки твердих матеріалів надається економічно більш вигідним (наприклад, пробивання каліброваних отворів у діаманті лазерним променем скоротило час із 24 ч до 6-8 хв). Лазери застосовуються для швидкісного і точного виявлення дефектів у виробах, для найтонших операцій (наприклад, промінь СО₂-лазера в якості безкровного хірургічного ножу), для дослідження механізму хімічних реакцій і впливу на їхній хід, для одержання зверхчистих речовин. Широко застосовується лазерний поділ ізотопів, наприклад, такого важливого в енергетичному відношенні елемента, як уран.

Одним із важливих застосувань лазерів є одержання і дослідження високотемпературної плазми. Ця галузь застосування пов’язана з розвитком нового напрямку лазерного керування термоядерного синтезу.

Лазери широко застосовуються у вимірювальній техніці. Лазерні інтерферометри(у них джерелом світла є лазер) використовуються для зверх точних дистанційних вимірів лінійних переміщень, коефіцієнтів заломлення середовища, тиску, температури.

6 Хід роботи

 

6.1 Включити лазер. Спрямувати промінь на дифракційну решітку, одержати дифракційний спектр монохроматичного випромінювання.

6.2 Спрямувати на дифракційну решітку промінь білого світла. Порівняти з отриманим у попередньому досліді. Відмінності записати у висновку1.

6.3 Спрямувати на призму промінь лазера, а потім промінь білого світла. Відмінності, що спостерігаєте, записати у висновку2.

6.4 Увисновку3 записати відмінності дифракційного та дисперсійного спектрів.

 

7 Контрольні питання

7.1 Сформулювати постулати Бора (та вивчити).

7.2 Основні компоненти лазеру та їх призначення.

7.3 Які стани називаються станами з інверсною заселеністю? Як здійснюються такі стани в ОКГ.

7.4 Які властивості лазерного випромінювання ви знаєте, який ККД лазерів?

7.5 Де застосовуються лазери?

7.6 Дати поняття та означення явищ: інтерференція, дифракція, дисперсія.

 

Висновок

зробити три висновки згідно ходу роботи.

 

9 Домашнє завдання

9.1 Поглинання. Спонтанне та вимушене випромінювання (Л.1.,с434)

9.2 Оптичні квантові генератори (Л1.,с436)

 

10 Література

Трофимова Т.И. Курс физики: Учеб. пособие для вузов. 1990.

 

Додаток А.

НАЙВАЖЛИВІШІ ФІЗИКО-ХІМІЧНІ КОНСТАНТИ

 

Атомна одиниця маси	1 а.о.м. = 1,66057 .10-27 кг 6,022169 .1023 а.о.м. = 1г
Заряд електрона	e– = 1,6022 .10-19 Кл
Маса спокою нейтрона	mn = 1,00866 а.о.м. = 1,67495 .10-24 г
Маса спокою протона	mр = 1,00728 а.о.м. = 1,67265 .10-24 г
Маса спокою електрона	mе = 5,48580 .10-4 а.о.м. = 9,10953 .10-28 г
Універсальна газова стала	R = 8,3144 = 0,082057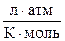
СталаБольцмана	k = 1,38066 .10-23 Дж/К
Стала Планка	h = 6,6262 .10-34 Дж .с
Стала Фарадея	F = Ne = 9,6485 .104 = 26,8
Число Авогадро	NА = 6,022045 .1023 моль-1
Число p (пі)	p = 3,1415926536

Густина твердих тіл

Значения густини дано при температурі 20

речовина речовина ,кг/м

Алмаз Асфальт Бетон Бумага писчая Винипласт Воск Гранит Графит Графит реакторный Земля Камфара Капрон Канифоль Кварц Корунд Кость >>слоновая Лава вулканическая Лавсан Лед (при t=0 C) Кирпич обыкновенный >> огнеупорный Линолеум Мел Медный купорос кристаллический Менделеевская замазка Мрамор Нафталин Нашатырь Парафин Плексиглас	1100-2800 1800-2800 700-1100 1350-1400 870-990 2500-3000   1650-1720 1300-2000 1070-1100 2500-2800 3950-4100 1700-2000   2000-3000 1300-1400 880-920   1400-1600   1700-2000 1250-1300 1800-2600   2200-2300   2600-2800 1500-1600 870-920	Полистирол Полиэтилен Пробка Ртуть твердая (при t=-38.9 С) Сахар-рафинад Сера Рубин Соль поваренная Сталь Стеарин Стекло бутылочное >> зеркальное >> оконное >> хрусталь Сургуч Сухой лед Текстолит Уголь древесный Уголь каменный Фибра Фарфор Фаянс хозяйственный и санитарно-технический Фосфор белый >> красный Фторопласт-4 Целлулоид Чугун серый Шифер Эбонит Янтарь	1050-1070 920-960 220-260   1930-2070 2150-2170 7600-7900 970-1000 2450-2720 2400-2700 2900-3000 1300-1400 300-600 1200-1500 2200-2500   1860-2200 2100-2300 6600-7200 1100-1200 1050-1090

Густина металів (при t=20 C)

Метал		Метал		Метал
Алюминий Бериллий Бор Ванадий Висмут Вольфрам Германий Железо Золото Индий Иридий Калий	2698,9 1847,7	Кобальт Литий Магний Марганец Медь Молибден Натрий Никель Ниобий Олово Осмий Платина	968,4	Плутоний Ртуть Свинец Серебро Тантал Титан Торий Уран Хром Цезий Цинк Цирконий	13546,2

 

 

Оцінка за лабораторну роботу

Оцінка «5» ставиться тоді, коли студент:

виконує роботу у повному обсязі з дотриманням необхідної послідовності проведення дослідів та вимірювань;

самостійно і раціонально монтує необхідне обладнання, всі досліди проводить у режимах, що забезпечують одержання правильних результатів і висновків, дотримується правил безпеки праці;

у звіті правильно і акуратно виконує всі записи, таблиці, малюнки, креслення, графіки, розрахунки;

вірно обґрунтовує теоретичні положення, закони, формулює фізичні поняття;

Оцінка «4» правомірна тоді, коли виконання вимоги до роботи на оцінку “5”, але учень припустився несуттєвих помилок або прорахунків, несуттєвих помилок при обґрунтуванні теоретичних положень, законів, формулюванні фізичних понять;

Оцінка «3» ставиться, якщо результат виконаної частини такий, що дозволяє одержати правильні висновки, але в ході проведення досліду і вимірювань були припущенні прорахунки;

формулює окремі закони, фізичні поняття з припущенням помилок;

Оцінка «2» ставиться тоді, коли результати не дають можливості одержати правильні висновки, тому що досліди, вимірювання, обчислення, спостереження виконувалися неправильно.

Оцінка «1» ставиться в тих випадках, коли учень зовсім не виконав роботу.

У всіх випадках оцінка знижується, якщо учень не дотримався вимог безпеки праці.