Алгебраическое представление двоичных чисел

Знак числа обычно кодируется двоичной цифрой, при этом код 0 означает знак +(плюс), код 1 — знак - (минус). Для алгебраического представления чисел, то есть для представления чисел с учетом их знака, в вычислительных машинах используются специальные коды:

- прямой код числа;

- обратный код числа;

- дополнительный код числа.

При этом два последних кода позволяют заменить неудобную для компьютера операцию вычитания на операцию сложения с отрицательным числом.

Дополнительный код обеспечивает более быстрое выполнение операций, поэтому в компьютере применяется чаще именно он.

1. Прямой код числа N — [ N ] _пр. Пусть N = а₁ а₂ а₃ …. а_т. Тогда

§ если N > 0, то [ N ] _пр = 0, а₁ а₂ а₃ …. а_т;

§ если N < О, то [ N ] _пр = 1, а₁ а₂ а₃ …. а_т;

§ если N = 0, то имеет место неоднозначность: [ 0 ] _пр = 0,0... или = 1;0...

Обобщая результаты, получим:

Если при сложении оба слагаемых имеют одинаковый знак, то операция сложения выполняется обычным путем. Если при сложении слагаемые имеют разные знаки, то сначала необходимо выявить большее по абсолютной величине число, произвести из него вычитание меньшего по абсолютной величине числа и разности присвоить знак большего числа.

Выполнение операций умножения и деления в прямом коде выполняется обычным образом, но знак результата определяется по совладению или несовпадению знаков участвовавших в операции чисел.

Операцию вычитания в этом коде нельзя заменить операцией сложения с отрицательным числом, поэтому возникают сложности, связанные с заемом значений из старших разрядов уменьшаемого числа. В связи с этим прямой код в компьютере почти не применяется.

2. Обратный код числа N — [N] _обр.

Обозначение означает величину, обратную a (инверсию а), то есть если а = 1, то а = 0, и наоборот.

§ если N > 0, то [N]_o6p=[N] _пр = 0, а₁ а₂ а₃ …. а_т;

§ если N < 0, то [N]_o6p = 1, ;

§ если N= 0, то неоднозначность, [0]_обр = 0,00...0 или = 1,11...1.

 

Для того чтобы получить обратный код отрицательного числа, необходимо все цифры этого числа инвертировать, то есть в знаковом разряде поставить 1, во всех значащих разрядах нули заменить единицами, а единицы нулями.

Например, число N =0,1011, [ N ] _обр =0,1011. Число N=- 0,1011, [N]_o6p =1,0100.

В случае, когда N < 0, [ N ] _обр = 10 - 1 • 10^-n + N, то есть [ N ] _обр = 1,1111+ N.

Обобщая результаты, получим

3. Дополнительный код числа N — [ N ] _дon.

§ если N ≤ 0, то [ N ] _дon =[ N ] _пр = 0, а₁ а₂ а₃ …. а_т;

§ если N ≥ 0, то [ N ] _o6p = 1, +0,00…1.

Для того чтобы получить дополнительный код отрицательного числа, необходимо все его цифры инвертировать (в знаковом разряде поставить единицу, во всех значащих разрядах нули заменить единицами, а единицы нулями) и затем к младшему разряду прибавить единицу. В случае возникновения переноса из первого после запятой разряда в знаковый разряд, к числу следует прибавить единицу в младший разряд.

Например, N = 0,1011, [ N ] _дon = 0,1011; N = -0,1100, [ N ] _дon = 1,0100;

N = -0,0000; [ N ] _дon = 10,0000 = 0,0000 (1 исчезает). Неоднозначности в изображении 0 нет.

Обобщая, можно записать:

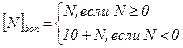
Прочие системы счисления

Кроме рассмотренных выше систем счисления, применяемых внутри компьютера, программисты и пользователи часто используют при работе с компьютерами также двоично-десятичную и шестнадцатеричную системы.