ВВЕДЕНИЕ
В настоящее время, быстрого развития компьютерной техники, сотовой телефонии, линий связи и передачи информации, существует острая связь в понимании и практическом применении способов кодирования и декодирования информации.
Аналого-цифровой преобразователь (АЦП) осуществляет преобразование аналогового сигнала (непрерывный спектр), в сигнал с дискретной формой значений. Цифро-аналоговый преобразователь (ЦАП) производит обратное преобразование цифрового (дискретного) сигнала в аналоговый.
Например, путём преобразования в цифровую форму с помощью АЦП, расположенного у источника информации, таких реально существующих переменных, как, температура, скорость и звук, и последующего восстановления тех же самых сигналов с помощью ЦАП, расположенном на оконечном устройстве.
Преимущества цифровых методов обработки информации могут быть реализованы лишь в том случае, когда АЦП и ЦАП не вносят в эту обработку ограничений по точности и быстродействию эти ограничения удаётся свести к минимуму при использовании интегральных АЦП и ЦАП. Интеграция схем преобразователей не только существенно улучшила экономические и надёжностные показатели АЦП и ЦАП, уменьшила их габариты с одновременным совершенствованием конструктивного исполнения, но и повысила быстродействие и метрологические характеристики за счёт уменьшения паразитных связей (внутренних емкостей), использования взаимной компенсации и идентичности отдельных элементов интегральных схем.
В зависимости от метода преобразования и способа его реализации разработано много АЦП различных типов (АЦП параллельного преобразования, АЦП двойного интегрирования и др.).
В данной работе рассматривается построение и принципы работы АЦП параллельного преобразования.
Построение схемы параллельного преобразования
Выбор схемы аналого-цифрового преобразования
Аналого-цифровые преобразователи (АЦП) предназначены для преобразования аналоговых (непрерывных) сигналов в цифровую форму. Преобразование аналогового сигнала происходит в определенные моменты времени, которые называются точками отсчета. Количество отсчетов за единицу времени определяет частоту дискретизации (преобразования), которая, в свою очередь, определяется быстродействием и условиями использования АЦП. Интервал времени между отсчетами Тотс и частота дискретизации fпр связаны соотношением:
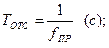
В измерительной технике для преобразования медленно меняющихся процессов частота преобразования может быть установлена небольшой - единицы Герц и менее. В устройствах, где требуется преобразовывать сигналы в масштабе реального времени, частота преобразования выбирается из условия достижения максимальной точности восстановления цифрового сигнала в аналоговую форму. Например, преобразование речевого сигнала в дискретную форму. При этом частота дискретизации определяется как fпр = 2Fмах, где Fмах - максимальная частота речевого сигнала.
Для обеспечения преобразования без искажений требуется выполнение условия:

где tпр - время преобразования АЦП одного отсчета.
Наибольшим быстродействием обладают АЦП прямого преобразования. Время преобразования tпр достигает 10 -20 нсек. Они используются для преобразования сигналов сверхбыстро протекающих процессов и сигналов телевизионного изображения (цифровое телевидение). Они отличаются высокой стоимостью и большой потребляемой мощностью. Функциональная схема АЦП прямого преобразования приведена на рис.1.

Рисунок 1.1 – Функциональная схема АЦП параллельного преобразования
Она содержит 2n компараторов, делитель опорного напряжения и преобразователь позиционного кода в параллельный двоичный код. Промышленностью выпускаются 4, 6, 8 - разрядные АЦП прямого преобразования. Время преобразования этих АЦП определяется исключительно только временем распространения сигнала в компараторах tздкр и преобразователе кодов tздпр, т.е. tпр = tздкр + tздпр.
Рисунок 1.2 показывает упрощенную блок-схему 3-х разрядного параллельного АЦП (для преобразователей с большим разрешением принцип работы сохраняется). Здесь используется массив компараторов, каждый из которых сравнивает входное напряжение с индивидуальным опорным напряжением. Такое опорное напряжение для каждого компаратора формируется на встроенном прецизионном резистивном делителе. Значения опорных напряжений начинаются со значения, равного половине младшего значащего разряда (LSB), и увеличиваются при переходе к каждому следующему компаратору с шагом, равным VREF /23. В результате для 3-х разрядного АЦП требуется 23-1 или семь компараторов. А, например, для 8-разрядного параллельного АЦП потребуется уже 255 (или (28-1)) компараторов.
С увеличением входного напряжения компараторы последовательно устанавливают свои выходы в логическую единицу вместо логического нуля, начиная с компаратора, отвечающего за младший значащий разряд. Можно представить преобразователь как ртутный термометр: с ростом температуры столбик ртути поднимается. На рис. 2 входное напряжение попадает в интервал между V3 и V4, таким образом 4 нижних компаратора имеют на выходе "1", а верхние три компаратора - "0". Дешифратор преобразует (23-1) - разрядное цифровое слово с выходов компараторов в двоичный 3-х разрядный код.
Параллельные АЦП - достаточно быстрые устройства, но они имеют свои недостатки. Из-за необходимости использовать большое количество компараторов параллельные АЦП потребляют значительную мощность, и их нецелесообразно использовать в приложениях с батарейным питанием.

Рисунок 1.2 - Схема 3 разрядного АЦП параллельного преобразования
Идеальная передаточная характеристика АЦП
Передаточная характеристика АЦП - это функция зависимости кода на выходе АЦП от напряжения на его входе. Такой график представляет собой кусочно-линейную функцию из 2N "ступеней", где N - разрядность АЦП. Каждый горизонтальный отрезок этой функции соответствует одному из значений выходного кода АЦП (см. рисунок 1.3). Если соединить линиями начала этих горизонтальных отрезков (на границах перехода от одного значения кода к другому), то идеальная передаточная характеристика будет представлять собой прямую линию, проходящую через начало координат.

Рисунок 1.3 – Идеальная передаточная характеристика 3- х разрядного АЦП






