А. Системы балочного типа

Рис. 1.19

Пример 1.1. Кинематический анализ балки и рамы (рис.1.19, а,б) производится по следующей схеме.

1. Подсчитываем число степеней свободы по формуле (1.1). При этом число дисков (Д) = 1; шарниров нет; количество опорных связей (С₀) = 3. Подставив в формулу, получим: W=3*1-3=0.

Вывод: возможно, что система СО и ГН.

Рис. 1.20

Каждый стержневой элемент опоры можно считать стержнем 1-го вида. Тогда мы придем к стандартному случаю соединения двух дисков в ГН систему: Диски связаны при помощи трёх стержней, не пересекающихся в одной точке и не параллельных между собой.

3. Окончательный вывод: Система ГН и СО

Пример 1.2. Кинематический анализ фермы (рис. 1.19 ,в) в более сложен:

1. Подсчитываем число степеней свободы по формуле (1.2) здесь количество стержней С= 25; количество узлов У= 14; количество опорных связей С₀= 3. Подставляя в формулу, получим: W=2*14-25-3=0

Вывод: возможно система ГН и СО.

2. Кинематический анализ фермы по её образованию. Необходимо сначала доказать, что сама ферма, представляющая собой шарнирное соединение стержней, является диском. А затем рассмотреть, как этот диск соединяется с землёй. Здесь каждый элемент (стержень) фермы является диском. Анализ удобнее производить по следующей схеме: принимаем любой стержень фермы за базовый диск (здесь это левая стойка – Диск 1). Далее считаем, что к этому диску присоединена диада (стержни, помеченные штрихом), следовательно, образовался новый диск из трёх стержней. К этому диску присоединяется новая диада (стержни, помеченные двумя штрихами) – образуется новый диск из 5 стержней и т.д. Для левой полуфермы диады обозначены значками. Таким образом, анализ по образованию фермы можно сформулировать так: Ферма образована последовательным присоединением диад к диску 1, следовательно, она ГИ и представляет собой диск.

Этот диск связан с землей тремя связями, не пересекающимися в одной точке и не параллельными между собой. Окончательный вывод: Система ГН и СО.

Рис. 1.21

Подчеркнём общие положения, связанные с кинематическим анализом систем балочного типа. Если доказано, что сама система является диском, она должна иметь как минимум 3 связи с землей. Эти связи не должны быть параллельны между собой и не должны пересекаться в одной точке.

Б. Составные системы

Примеры составных систем показаны на рис. 1.22. Это могут быть составные рамы, балки, фермы, арки.

Второстеп. диск

Все системы, показанные на рис. 1.22, образованы по одному принципу. Главный диск связан с землей тремя связями. Второстепенный диск присоединен к главному при помощи шарнира (рис.1.23, а), либо при помощи двух стержней (рис.1.23, б) и имеет одну связь с землей. На рис. 1.23 схематично показаны системы, имеющие один или несколько второстепенных дисков, присоединенных последовательно один через другой (рис. 1.23, в), либо только к главному диску (рис.1.23, г)

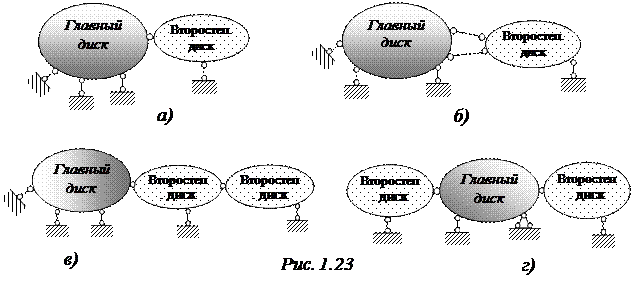
Число степеней свободы W для всех схем, показанных на рис. 1.22, 1.23 равно 0. Например, для системы, показанной на рис. 1.21, г число дисков Д =3, число шарниров Ш=2, а число опорных связей С₀=5. Тогда получаем

W=3*3-2*2-5=0.

Аналогично можно подсчитать W для всех остальных схем.

Кинематический анализ по образованию таких систем выполняется по следующей схеме:

1). Сначала доказывается, что Главный диск и Земля образуют общий диск (они связаны тремя связями). 2). Второстепенный диск присоединяется к этому вновь образованному диску при помощи шарнира и стержня (либо при помощи трёх стержней). Если имеется несколько второстепенных частей, рассматривается присоединение каждой по той же схеме. Вывод: Система в целом является диском.

Подчеркнём общие положения, связанные с кинематическим анализом составных систем. Главный диск должен иметь как минимум 3 связи с землей. Эти связи не должны быть параллельны между собой и не должны пересекаться в одной точке. Если второстепенный диск связан с главным шарниром, то ось стержня, соединяющего второстепенный диск с Землёй не должен пересекать этот шарнир. В противном случае система Мгновенно изменяема (рис 1.24, а).

Если второстепенный диск связан с главным двумя стержнями, то оси этих стержней, и ось опорного стержня, соединяющего второстепенный диск с Землёйне должны пересекаться в одной точке. В противном случае система Мгновенно изменяема (рис 1.24, б).

В. Трёхшарнирные системы

Примеры трёхшарнирных систем показаны на рис 1.25.

Трёхшарнирные системы состоят из двух дисков, которые связаны шарниром. К Земле каждый диск присоединяется шарнирно неподвижной опорой.

Схематично такая система показана на рис. 1.26, а. Вместо шарнира соединение дисков может производиться двумя стержнями (рис 1.26, б).

Кинематический анализ систем, где диски связаны шарниром (рис. 1.26, а). производится следующим образом.

1. Определяется число степеней свободы по формуле (1.1). Здесь число дисков (Д) = 2, Число шарниров (Ш) = 1 Опорных связей (С₀) = 4. Подставив в формулу, получим W=3*2-2*1-4 =0

Вывод: возможно, что система СО и ГН.

2. Анализ по образованию:

Включаем Землю как диск (рис. 1.27). Опоры А и В можно показать в виде шарниров, присоединённых к земле. Тогда мы получаем 3 диска, связанных при помощи трёх шарниров (А,В,С). Система в целом является СО и ГН. При этом опорные шарниры А, В и шарнир С не должны лежать на одной прямой.

Трёхшарнирные системы с затяжкой

В этом случае одна опора становится шарнирно-подвижной. Недостающая связь устанавливается как внутренняя и соединяет диски. Примеры трёхшарнирных систем с затяжкой показаны на рис.1.28.

Рис. 1.28

Кинематический анализ производится по следующей схеме.

1. Определяется число степеней свободы по формуле (1.1) Здесь число Дисков (Д) = 3, Число шарниров (Ш) = 3. Опорных связей (С₀) = 3. Подставив в формулу, получим W=3*3-2*3-3 =0

Вывод: возможно, что система СО и ГН.

2. Анализ по образованию системы: Включаем Землю как диск. Диск 1 и Диск 2 связаны шарниром С и стержнем АВ (ось стержня не пересекает шарнир). Следовательно, они образуют общий диск. Этот диск связан с землей тремя связями, которые не пересеваются в одной точке и не

параллельны между собой. Система в целом является СО и ГН.

Пример 1.3. Кинематического анализа составной статически определимой балки (рис. 1.30)

Рис. 1.30

1. Подсчитываем число степеней свободы по выражению (1.1). Число дисков (Д) – 5; шарниров (Ш) – 4; число опорных связей (С₀) – 7.

Тогда W=3*5-2*4-7=0

Вывод: Возможно, система СО и ГН.

2. Выполняем анализ балки по её образованию. При этом землю принимаем за дополнительный диск.

Выделим диски, на которые делится сама балка (AB, CD, DE,EF) и диск-Землю. Соединения этих дисков должны хорошо просматриваться. Это опорные связи (G,H,K,L), шарнир (D). Диск BC также принимаем за связь, так как он связывает между собой два диска (AB и CD) и не связан с землёй.

Рассмотрим теперь соединения этих дисков. Будем укрупнять их, пока не докажем, что вся балка является диском. Напомним, что диском называется часть системы или вся система целиком, если её геометрическая неизменяемость доказана. Начнём с того, что диск АВ и диск Земля связаны жестко, следовательно, образуют один общий диск. Обозначим его Д1 и обведём пунктиром.

Далее рассмотрим соединения трёх дисков: Д1, CD и DE. Диски CD и DE соединены шарниром (D), диски Д1 и CD двумя стержнями (BC и G), и наконец, диски DE и Земля соединены двумя стержнями (H и K). В целом получается соединение трёх дисков при помощи шарнира и четырёх стержней. Такой стандартный способ соединения трёх дисков есть. Однако необходимо доказать, что система не является мгновенно изменяемой. Для этого определим положение фиктивных шарниров, которые находятся на пересечении стержней. Это шарнир Ш1 (на пересечении стержней BC и G) и шарнир, положение которого уходит в бесконечность, т.к. стержни H и K параллельны. Шарниры не лежат на одной прямой. Таки образом мы доказали, что диски Д1, CD и DE образуют общий диск. Обозначим его Д2 и обведём точечной линией.

Диск Д2 связан c диском EF шарниром E и стержнем L (стержень не пересекает шарнир). Таким образом, они образуют общий диск.

Окончательный вывод: система в целом является диском, следовательно, она ГН и СО.

Контрольные вопросы к разделу 1

1. Какие системы называются геометрически неизменяемыми?

2. Каков порядок кинематического анализа систем? Количественная и качественные оценки неизменяемости системы.

3. Покажите на примерах простейшие способы образования геометрически неизменяемых систем.

4. Какие системы называются мгновенно изменяемыми?

5. Приведите пример системы близкой к мгновенно изменяемой.

6. Назовите основные типы опорных устройств, их статические и кинематические характеристики.

7. Почему сооружение называется статически определимым?

Пример теста на защиту темы:

1. Число степеней свободы рамы равно (1)

Рама является: (1)

- Статически определимой - Статически неопределимой - Геометрически изменяемой - Мгновенно изменяемой

Сколько связей нужно удалить

в рамах, чтобы они стали статически определимыми? (2)

Удаление какой пронумерованной связи

сделает систему мгновенно изменяемой? (1)

Какое минимальное число опорных

связей нужно добавить, чтобы рама стали геометрически неизменяемыми? (2)

Удаление какой пронумерованной связи

сделает систему геометрически изменяемой? (1)

7. Число степеней свободы фермы равно (1)

8. Сколько шарниров нужно добавить, чтобы балка стала статически определимой? (1)