1) Последовательно выполнить деление данного числа и получаемых неполных частных на основание новой системы счисления до тех пор, пока не получите неполное частное, меньшее делителя;
2) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
3) составить число в новой системе счисления, записывая его, начиная с последнего частного.
П 1.18. Перевести число 3710 в двоичную систему счисления. Для обозначения цифр в записи числа используем символику: а5 а4 а3 а2 а1 а0.



 Отсюда 3710 = 1001012.
Отсюда 3710 = 1001012.
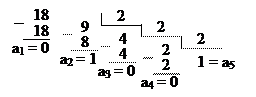 |
П 1.19. Перевести десятичное число 315 в восьмеричную и в шестнадцатеричную системы счисления:
 |  |
Отсюда следует: 31510 = 4738 = 13В16.
Напомним, что 1110 = В16.
Перевод двоичных чисел в системы счисления с основанием 2n
Для того, чтобы целое двоичное число записать в системе счисления с основанием q = 2 n (4, 8, 16 и т.д.), нужно:
1) данное двоичное число разбить справа налево на группы по n цифр в каждой группе;
2) если в последней левой группе окажется меньше n разрядов, то ее надо дополнить слева нулями до нужного числа разрядов;
3) рассмотреть каждую группу как n -разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q = 2 n.
Ниже приводится таблица с числами систем счисления с основаниями q = 2 n, где n = 1, 3, 4 и десятичной системы счисления.
| Десятичная | Двоичная | Восьмеричная | Шестнадцатеричная |
| А | |||
| B | |||
| C | |||
| D | |||
| E | |||
| F |
П 1.20. Перевести число 11001010011010101112 в восьмеричную систему счисления.
Разбиваем число на группы по три цифры – триады (т.к. q = 8, 8 = 2 n, n = 3) справа налево и, пользуясь таблицей, записываем соответствующее восьмеричное число.
Ответ: 14515278
П 1.21. Перевести число 11001010011010101112 в шестнадцатеричную систему счисления.
Разбиваем число на группы по четыре цифры – тетрады (т.к. q = 16, 16 = 2 n, n = 4) справа налево и, пользуясь таблицей, записываем соответствующее шестнадцатеричное число.
Ответ: 6535716
П 1.22. Чему равно значение основания системы счисления Х, если известно, что 175 Х = 7D16?
Решение: Запишем числа 175 Х и 7D16 в десятичной системе счисления.
175 Х = Х 2 + 7 Х + 5,
7D16 = 7·16 + 13 = 125.
Но так как эти числа равны, то Х 2 + 7 Х + 5 = 125.
Корни полученного квадратного уравнения: Х = 8 и Х = -15 (не подходит, так как основание системы счисления не может быть отрицательной величиной). Следовательно, основание системы счисления – 8.
Для того, чтобы произвольное число, записанное в системе счисления с основанием q = 2 n, перевести в двоичную систему счисления, нужно каждую цифру этого числа заменить ее n -разрядным эквивалентом в двоичной системе счисления.
Применительно к компьютерной информации часто используются системы с основанием 8 (восьмеричная) или 16 (шестнадцатеричная).
П 1.23. Перевести двоичное число 110111101011101111 в шестнадцатеричную систему счисления.
Решение:Разделим данное число на группы по четыре цифры, начиная справа. Если в крайней левой группе окажется меньше четырех цифр, то дополним ее нулями
0011 0111 1010 1110 1111.
А теперь, глядя на двоично-шестнадцатеричную таблицу, заменим каждую двоичную группу на соответствующую шестнадцатеричную цифру
3 7 А Е F.
Следовательно
1101111010111011112 = 37AEF16.
Тестовые задачи
Т 1.21. В саду 100 q плодовых кустарников, из них 33 куста малины, 22 куста смородины красной, 16 кустов черной смородины и 17 кустов крыжовника. В какой системе счисления подсчитаны деревья?
Варианты ответа: а) 7; б) 9; в) 11; г) 13.
Т 1.22. Было 53 q груши. После того, как каждую из них разрезали пополам, стало 136 половинок. В системе счисления с каким основанием вели счет?
Варианты ответа: а) 11; б) 13; в) 15; г) 17.
Т 1.23. Какое число больше?
Варианты ответа: а) 1527; б) 15210; в) 15212; г) 15216.
Т 1.24. Переведите двоичные числа в восьмеричную систему счисления:
а) 110000110101; 1010101 б) 11100001011001; 1000010101.
Т 1.25. Переведите двоичные числа в шестнадцатеричную систему счисления: а) 11011010001; 111111111000001 б) 10001111010; 100011111011.
Т 1.26. Переведите шестнадцатеричные числа в двоичную систему счисления: а) 1АС7 б) FACC.
Т 1.27. Переведите числа из восьмеричной системы счисления в шестнадцатеричную: а) 774; б) 665.






