ЭЛЕКТРОМАГНЕТИЗМ
Электростатика
1. Два одноименных заряда Q 1=0,7 нКл и Q 2=1,3 нКл находятся в воздухе на расстоянии r =6 см друг от друга. На каком расстоянии между ними нужно поместить третий заряд, чтобы результирующая сила, действующая на каждый заряд, была равна нулю?
2. Три одинаковых заряда q =1 нКл каждый расположены по вершинам равностороннего треугольника. Какой отрицательный заряд q 1 нужно поместить в центре треугольника, чтобы его притяжение уравновесило силы взаимного отталкивания зарядов?
3. Два точечных одинаковых заряда (q =1,1 нКл) находятся на расстоянии 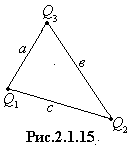 r =17 см друг от друга. С какой силой и в каком направлении они действуют на положительный единичный заряд, находящийся на таком же расстоянии от каждого из них?
r =17 см друг от друга. С какой силой и в каком направлении они действуют на положительный единичный заряд, находящийся на таком же расстоянии от каждого из них?
4. 4. Одноименные заряды Q 1 =0,2 мКл, Q 2 =0,5 мКл и Q 3=0,4 мКл расположены в вершинах треугольника со сторонами а =4 см, b =5 см, с =7 см (рис.3.).Определить модуль и направление силы, действующей на заряд Q 3.
5. В центре квадрата расположен положительный заряд 250 нКл. Какой отрицательный заряд надо поместить в каждой вершине квадрата, чтобы система зарядов находилась в равновесии?
6. В вершинах и в центре правильного треугольника со стороной 5 см расположены положительные одинаковые заряды 0,5 мКл каждый. Какая сила действует на отрицательный заряд 0,7 мКл, находящийся на продолжении высоты, на расстоянии 7 см от вершины?
7.  В вершинах шестиугольника помещены положительные одинаковые заряды 10 нКл каждый. Какой отрицательный заряд надо поместить в центре шестиугольника, чтобы результирующая сила, действующая на каждый заряд, была равна нулю?
В вершинах шестиугольника помещены положительные одинаковые заряды 10 нКл каждый. Какой отрицательный заряд надо поместить в центре шестиугольника, чтобы результирующая сила, действующая на каждый заряд, была равна нулю?
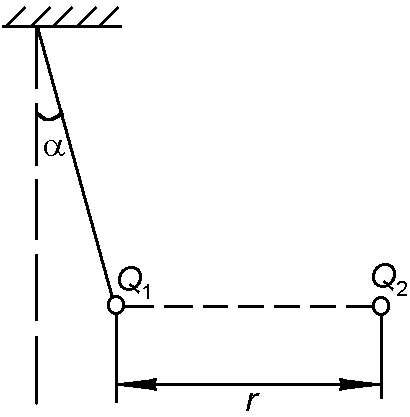
8. Шарик массой m = 4 г, несущий заряд 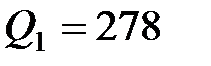 нКл, подвешен в воздухе на невесомой нерастяжимой непроводящей нити. При приближении к нему заряда Q 2 противоположного знака нить отклонилась на угол a = 45° от вертикального направления (рис.4.). Найти модуль заряда Q 2 , если расстояние r = 6 см.
нКл, подвешен в воздухе на невесомой нерастяжимой непроводящей нити. При приближении к нему заряда Q 2 противоположного знака нить отклонилась на угол a = 45° от вертикального направления (рис.4.). Найти модуль заряда Q 2 , если расстояние r = 6 см.
9. В модели атома Бора-Резерфорда электроны движутся по круговым орбитам вокруг положительно заряженного ядра. Определить скорость 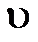 и ускорение а электрона в атоме водорода, если радиус боровской орбиты r = 52,9 пм.
и ускорение а электрона в атоме водорода, если радиус боровской орбиты r = 52,9 пм.
10. Два шарика массой m = 0,1 г каждый подвешены в одной точке на нитях длиной 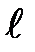 = 20 см каждая. Получив одинаковый заряд, шарики разошлись так, что нити образовали угол между собой
= 20 см каждая. Получив одинаковый заряд, шарики разошлись так, что нити образовали угол между собой 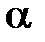 = 60°. Найти заряд каждого шарика.
= 60°. Найти заряд каждого шарика.
11. Даны два шарика m = 1 г каждый. Какой заряд Q нужно сообщить каждому шарику, чтобы сила взаимного отталкивания зарядов уравновесила силу взаимного притяжения шариков по закону тяготения Ньютона? Рассматривать шарики как материальные точки.
12. Расстояние между двумя точечными зарядами Q 1 = 1 мкКл и Q 2 = – Q 1 равно 10 см. Определите силу F, действующую на точечный заряд 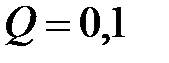 мкКл, удаленный на r 1 = 6 см от первого и на r 2 = 8 см от второго зарядов.
мкКл, удаленный на r 1 = 6 см от первого и на r 2 = 8 см от второго зарядов.
13. Два одинаковых проводящих заряженных шара находятся на расстоянии r = 60см. Сила отталкивания шаров F 1 = 10 мкН. После того, как шары привели в соприкосновение и удалили друг от друга на прежнее расстояние, сила отталкивания возросла и стала равной F 2 = 160 мкН. Вычислить заряды Q 1 и Q 2, которые были на шарах до их соприкосновения. Диаметр шаров считать много меньше расстояния между ними.
14. Два одинаковых проводящих шара находятся на расстоянии  см. Сила притяжения шаров F 1 = 90 мкН. После того, как шары были приведены в соприкосновение и удалены друг от друга на прежнее расстояние, сила отталкивания стала равной F 2 = 160 мкН. Вычислить заряды Q 1 и Q 2, которые были на шарах до их соприкосновений. Диаметр шаров считать много меньше расстояния между ними.
см. Сила притяжения шаров F 1 = 90 мкН. После того, как шары были приведены в соприкосновение и удалены друг от друга на прежнее расстояние, сила отталкивания стала равной F 2 = 160 мкН. Вычислить заряды Q 1 и Q 2, которые были на шарах до их соприкосновений. Диаметр шаров считать много меньше расстояния между ними.
15. Два положительных точечных заряда Q и 4 Q закреплены на расстоянии
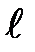 = 60 см друг от друга. В какой точке на прямой, проходящей через заряды, следует поместить третий заряд Q 1, чтобы он находился в равновесии?
= 60 см друг от друга. В какой точке на прямой, проходящей через заряды, следует поместить третий заряд Q 1, чтобы он находился в равновесии?
16. Расстояние между свободными зарядами Q 1 = 150 нКл и Q 2 = 720 нКл равно 60 см. Определить точку на прямой, проходящей через заряды, в которой нужно поместить третий заряд Q 3 так, чтобы система зарядов находилась в равновесии. Определить величину и знак заряда.
17. Электрическое поле создано двумя точечными зарядами Q 1 = 10 нКл и
Q 2 = –20нКл, находящимися на расстоянии d = 20 см друг от друга. Определить напряженность E поля в точке, удаленной от первого заряда на r 1 = 30 см и от второго на r 2 = 50 см.
18. Расстояние между двумя положительными точечными зарядами Q 1 = 9 Q и Q 2= Q равно d = 8 см. На каком расстоянии r от первого заряда находится точка, в которой напряженность поля зарядов равна нулю? Где находилась бы эта точка, если бы второй заряд был отрицательным?
19. Тонкий стержень длиной 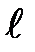 = 10 см равномерно заряжен. Линейная плотность заряда τ = 1 мкКл/м. На продолжении оси стержня на расстоянии а = 20 см от ближайшего его конца находится точечный заряд Q = 100 нКл. Определить силу F взаимодействия заряженного стержня и точечного заряда.
= 10 см равномерно заряжен. Линейная плотность заряда τ = 1 мкКл/м. На продолжении оси стержня на расстоянии а = 20 см от ближайшего его конца находится точечный заряд Q = 100 нКл. Определить силу F взаимодействия заряженного стержня и точечного заряда.
20. Тонкий длинный стержень равномерно заряжен с линейной плотностью τ= 10 мкКл/м. На продолжении оси стержня на расстоянии а = 20 см от его конца находится точечный заряд Q = 10 нКл. Определить силу F взаимодействия заряженного стержня и точечного заряда.
21. Два разноименно заряженных шарика находятся в масле на расстоянии 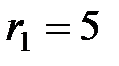 см. Определить диэлектрическую проницаемость масла, если эти шарики взаимодействуют с такой же силой в воздухе на расстоянии
см. Определить диэлектрическую проницаемость масла, если эти шарики взаимодействуют с такой же силой в воздухе на расстоянии 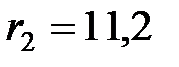 см.
см.
22. В центре правильного треугольника, в вершинах которого находится по заряду  Кл, помещен отрицательный заряд. Найдите величину этого заряда
Кл, помещен отрицательный заряд. Найдите величину этого заряда  , если данная система находится в равновесии.
, если данная система находится в равновесии.
23. Бесконечная вертикальная плоскость заряжена с поверхностной плотностью  . К плоскости на шелковой нити подвешен шарик массой
. К плоскости на шелковой нити подвешен шарик массой  г. Определить заряд шарика
г. Определить заряд шарика 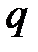 , если нить составляет угол
, если нить составляет угол 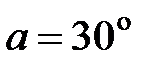 с плоскостью.
с плоскостью.
24. Два точечных заряда, равные 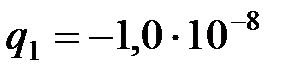 Кл и
Кл и 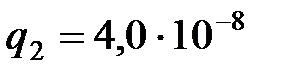 Кл, расположены на расстоянии
Кл, расположены на расстоянии 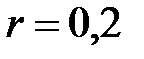 друг от друга в вакууме. Определить напряженность поля в точке посередине между зарядами, а также установить, на каком расстоянии
друг от друга в вакууме. Определить напряженность поля в точке посередине между зарядами, а также установить, на каком расстоянии 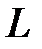 от положительного заряда напряженность поля равна нулю.
от положительного заряда напряженность поля равна нулю.
25. Положительно заряженный шарик массой  г и плотностью вещества
г и плотностью вещества 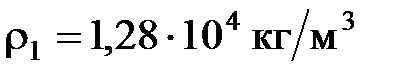 находится во взвешенном состоянии в жидком диэлектрике плотностью
находится во взвешенном состоянии в жидком диэлектрике плотностью 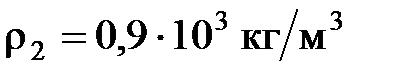 . В диэлектрике имеется однородное электрическое поле напряженностью
. В диэлектрике имеется однородное электрическое поле напряженностью  , направленное вертикально вверх. Найдите заряд шарика.
, направленное вертикально вверх. Найдите заряд шарика.
26. Электрон, летящий из бесконечности со скоростью  , остановился на расстоянии
, остановился на расстоянии  м от поверхности отрицательно заряженного металлического шара радиусом
м от поверхности отрицательно заряженного металлического шара радиусом 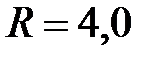 см. Определить потенциал шара. Заряд и масса электрона
см. Определить потенциал шара. Заряд и масса электрона  Кл,
Кл, 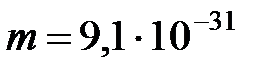 кг.
кг.
27. Шарик, заряженный до потенциала 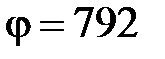 В имеет поверхностную плотность заряда
В имеет поверхностную плотность заряда 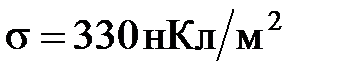 . Найти радиус шарика.
. Найти радиус шарика.
28. Электрон влетает в плоский воздушный конденсатор со скоростью 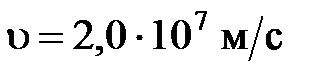 , направленной параллельно его пластинам, расстояние между которыми
, направленной параллельно его пластинам, расстояние между которыми 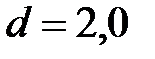 см. Найти отклонение электрона, вызванное полем конденсатора, если к пластинам приложена разность потенциалов
см. Найти отклонение электрона, вызванное полем конденсатора, если к пластинам приложена разность потенциалов  В, а длинна пластин
В, а длинна пластин  см. Удельный заряд электрона
см. Удельный заряд электрона  .
.
29. Два плоских воздушных конденсатора емкостью 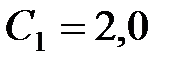 мкФ и
мкФ и  мкФ соединены параллельно, заряжены до разности потенциалов
мкФ соединены параллельно, заряжены до разности потенциалов 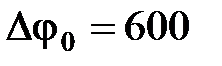 В и отключены от источника ЭДС. Затем расстояние между обкладками конденсатора
В и отключены от источника ЭДС. Затем расстояние между обкладками конденсатора 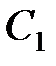 увеличили в
увеличили в  раз. Определить установившееся напряжение
раз. Определить установившееся напряжение  .
.
30. Конденсатор емкостью 6 мкФ последовательно соединен с конденсатором неизвестной емкости и они подключены к источнику постоянного напряжения 12 В. Определить емкость второго конденсатора и напряжения на каждом конденсаторе, если заряд батареи 24 мкКл.
31. Плоский воздушный конденсатор заряжен до разности потенциалов 300 В. Площадь пластин 1 см2, напряженность поля в зазоре между ними 300 кВ/м. Определить поверхностную плотность заряда на пластинах, емкость и энергию конденсатора.
32. Площадь пластин плоского слюдяного конденсатора 1,1 см2, зазор между ними 3 мм. При разряде конденсатора выделилась энергия 1 мкДж. До какой разности потенциалов был заряжен конденсатор?
33. Энергия плоского воздушного конденсатора 0,4 нДж, разность потенциалов на обкладках 600 В, площадь пластин 1 см2. Определить расстояние между обкладками, напряженность и объемную плотность энергии поля конденсатора.
34. В вершинах квадрата со стороной 0,1 м расположены равные одноименные заряды. Потенциал создаваемого ими поля в центре квадрата равен 500 В. Определить заряд.
35. В вершинах квадрата со стороной 0,5 м расположены заряды одинаковой величины. В случае, когда два соседних заряда положительны, а два других – отрицательные, напряженность поля в центре квадрата равна 144 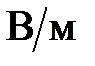 . Определить заряд.
. Определить заряд.
36. В вершинах квадрата со стороной 0,1 м помещены заряды по 0,1 нКл. Определить напряженность и потенциал поля в центре квадрата, если один из зарядов отличается по знаку от остальных.
37. На расстоянии 8 см друг от друга в воздухе находятся два заряда по 1 нКл. Определить напряженность и потенциал поля в точке, находящейся на расстоянии 5 см от зарядов.
38. Со скоростью 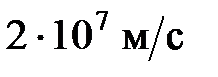 электрон влетает в пространство между обкладками плоского конденсатора в середине зазора в направлении, параллельном обкладкам. При какой минимальной разности потенциалов на обкладке электрон не вылетит из конденсатора, если длина конденсатора 10 см, а расстояние между его обкладками 1 см?
электрон влетает в пространство между обкладками плоского конденсатора в середине зазора в направлении, параллельном обкладкам. При какой минимальной разности потенциалов на обкладке электрон не вылетит из конденсатора, если длина конденсатора 10 см, а расстояние между его обкладками 1 см?
39. Заряд –1нКл переместился в поле заряда +1,5 нКл из точки с потенциалом 100 В в точку с потенциалом 600 В. Определить работу сил поля и расстояние между этими точками.
40. Две бесконечные параллельные плоскости находятся на расстоянии d = 0,5 см друг от друга. На плоскостях равномерно распределены заряды с поверхностными плотностями s1 = 0,2 мкКл/м2 и s2 = – 0,3 мкКл/м2. Определить разность потенциалов ∆ j между плоскостями.
Постоянный электрический ток
41. Определить плотность тока в железном проводе длиной 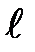 = 20 м, если провод находится под напряжением U = 12 В. Удельное сопротивление железа ρ = 9,8ּ10-8 Омּм.
= 20 м, если провод находится под напряжением U = 12 В. Удельное сопротивление железа ρ = 9,8ּ10-8 Омּм.
42. Напряжение на концах медного проводника длиной 1 м и сечением 1 мм2 меняется по закону  , где U 0 = 10 В, k = 0,1 с-1. Определить, сколько электронов пройдет через сечение проводника за 1 мин.
, где U 0 = 10 В, k = 0,1 с-1. Определить, сколько электронов пройдет через сечение проводника за 1 мин.
43. Определить число электронов, проходящих за время t = 1 с через поперечное сечение площадью S = 1 мм2 железной проволоки с удельным сопротивлением ρ = 9,8ּ10-8 Омּм, длиной 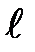 = 20 м при напряжении на ее концах U = 16 В.
= 20 м при напряжении на ее концах U = 16 В.
44. Какое напряжение можно дать на катушку, имеющую 1000 витков медного провода со средним диаметром витка d = 10 см, если допустимая плотность тока j = 2 А/мм2?
45. По медному проводнику сечением 1 мм2 течет ток 0,1 А. Найти среднюю скорость упорядоченного движения электронов, считая, что на каждый атом меди приходится один свободный электрон.
46. Участок электрической цепи составлен из трех кусков провода одинаковой длины, изготовленных из одного и того же материала, соединенных последовательно. Сечения кусков провод равны S 1 = 2 мм2, S 2 = 1 мм2 и S 3 = 3 мм2. Разность потенциалов на концах участка U = 12 В. Найти разность потенциалов на каждом куске провода.
47. ЭДС батареи ε = 12 В. Наибольшая сила тока, которую может дать батарея I max = 6 А. Определить максимальную мощность, которая может выделиться во внешней цепи.
48. ЭДС батареи ε = 16 В, внутреннее сопротивление r = 3 Ом. Найти сопротивление внешней цепи, если известно, что в ней выделяется мощность N = 16 Вт. Определить КПД батареи.
49. При включении электромотора в сеть с напряжением U = 220 В он потребляет ток I = 5 А. Определить мощность, потребляемую мотором, и его КПД, если сопротивление R обмотки мотора равна 6 Ом.
50. Батарея из двух параллельно соединенных источников с ЭДС 2 В и 1,8 В и внутренним сопротивлением 50 мОм каждый замкнута на сопротивление 2 Ом. Найти величину тока, проходящего через сопротивление и через источники.
51. Вольтметр, включенный в сеть последовательно с сопротивлением R 1, показал напряжение U 1 = 198 В, а при включении последовательно с сопротивлением R 2 = 2 R 1 – напряжение U 2 = 180 В. Определить сопротивление R 1 и напряжение в сети, если сопротивление вольтметра r = 900 Ом.
52. Сколько ламп мощностью по 300 Вт, предназначенных для напряжения 110 В, можно соединить параллельно, если проводка к ним от магистрали сделана медным проводом длиной 100 м и сечением 9 мм2, а напряжение в магистрали равно 220 В?
53. Трамвайный вагон потребляет ток 100 А при напряжении 600 В и развивает силу тяги 3000 Н. Определить скорость движения трамвая на горизонтальном участке пути, если КПД электродвигателя трамвая 80 %.
54. Элемент с ЭДС 2,1 В и внутренним сопротивлением 0,2 Ом соединен с реостатом. Определить силу тока в цепи, если напряжение на зажимах элемента 2 В. Какой длины надо взять для изготовления реостата железную проволоку сечением 1 мм2?
55. Сила тока в проводнике сопротивлением R = 10 Ом за время t = 50 с равномерно возрастает от I 1 = 5 А до I 2 = 10 А. Определить количество теплоты Q, выделившееся за это время в проводнике.
56. В проводнике за время t = 10 с при равномерном возрастании силы тока от I 1 = 1 А до I 2 = 2 А выделилось количество теплоты Q = 5 кДж. Найти сопротивление R проводника.
57. Три сопротивления 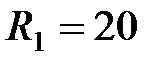 Ом,
Ом, 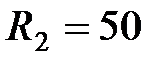 Ом и
Ом и 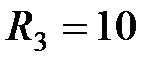 Ом соединены параллельно. Определить общий ток в цепи
Ом соединены параллельно. Определить общий ток в цепи 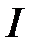 , если через второе сопротивление проходит ток
, если через второе сопротивление проходит ток 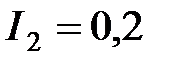 A.
A.
58.  Какова сила тяги тепловоза при скорости движения
Какова сила тяги тепловоза при скорости движения  , если его двигатель, имеющий кпд
, если его двигатель, имеющий кпд 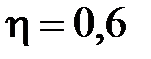 , работает при напряжении
, работает при напряжении 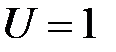 кВ и силе тока
кВ и силе тока 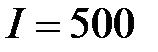 A?
A?
59. 59. Электрический нагреватель работает от сети с напряжением 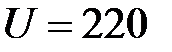 B при силе тока
B при силе тока 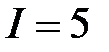 A и за
A и за  мин нагревает воду от
мин нагревает воду от 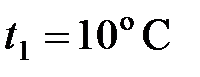 до
до 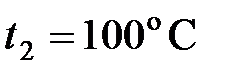 . Найти КПД нагревателя.
. Найти КПД нагревателя.
60. 60. В электрическую цепь включена лампочка, сопротивление которой 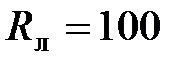 Ом. Найти мощность лампочки, если ЭДС источника тока
Ом. Найти мощность лампочки, если ЭДС источника тока  B, его внутреннее сопротивление
B, его внутреннее сопротивление 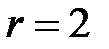 Ом. Внешнее сопротивление
Ом. Внешнее сопротивление 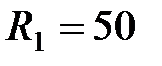 Ом.
Ом.
61. Электрический фонарь состоит из трех ( ) последовательно соединенных элементов (каждый из которых имеет ЭДС
) последовательно соединенных элементов (каждый из которых имеет ЭДС  В и внутреннее сопротивление
В и внутреннее сопротивление  Ом). Какую максимальную полезную мощность может сформировать батарея фонаря.
Ом). Какую максимальную полезную мощность может сформировать батарея фонаря.
62. Найти общее сопротивление участка цепи между точками А и В на рис. 2.4.17.
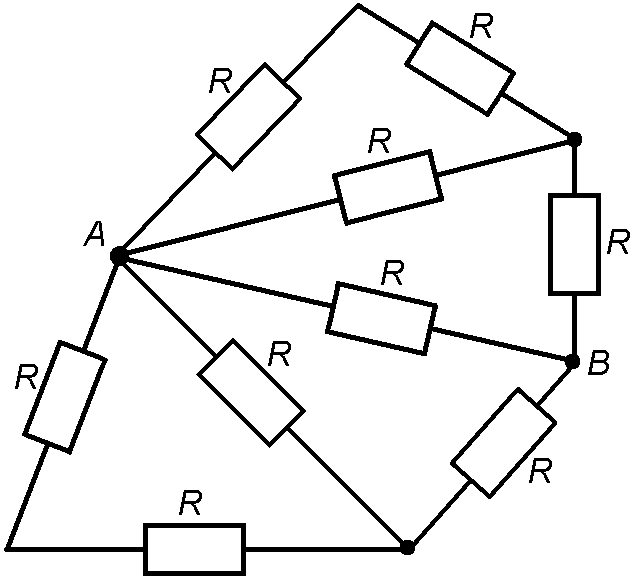
| 
|
Рис. 2.4.17 Рис. 2.4.19
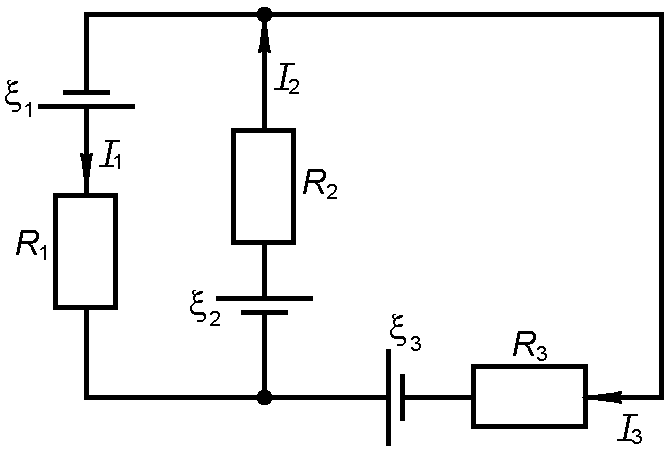
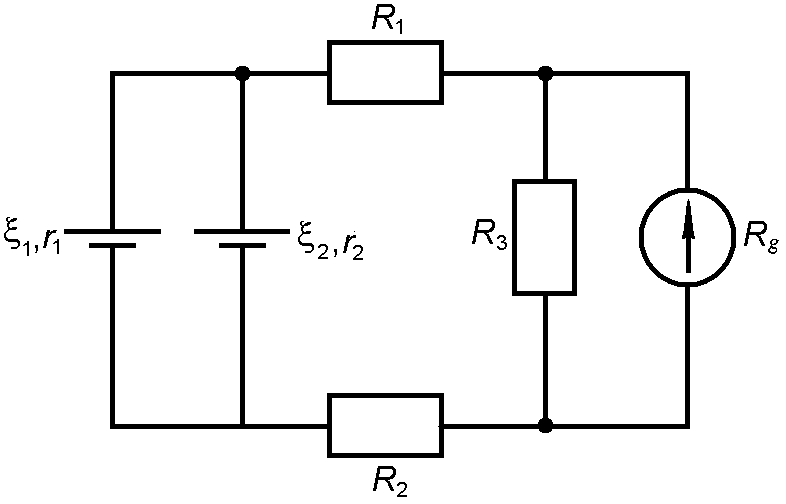
63. В цепи (рис. 2.4.19) найти силу тока в каждой ветви, если ЭДС источников тока равны  В,
В,  В,
В,  В, а сопротивления
В, а сопротивления 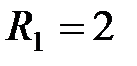 Ом,
Ом, 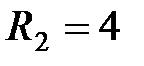 Ом,
Ом, 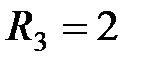 Ом. Внутренним сопротивлением источников пренебречь.
Ом. Внутренним сопротивлением источников пренебречь.

| 
|
Рис. 2.4.20 Рис. 2.4.21
64. Найти силу тока в цепи (рис. 2.4.20), если у каждого элемента ЭДС 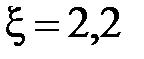 В и внутреннее сопротивление 20 Ом, а
В и внутреннее сопротивление 20 Ом, а  Ом,
Ом, 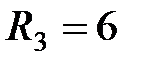 Ом,
Ом,  Ом,
Ом,  Ом.
Ом.
65. Найти силу тока гальванометра, включенного в цепь (рис. 2.4.21), если 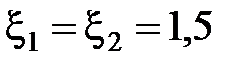 В;
В; 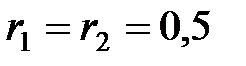 Ом,
Ом, 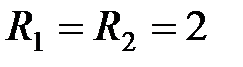 Ом,
Ом,  Ом,
Ом, 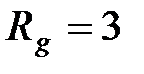 Ом.
Ом.
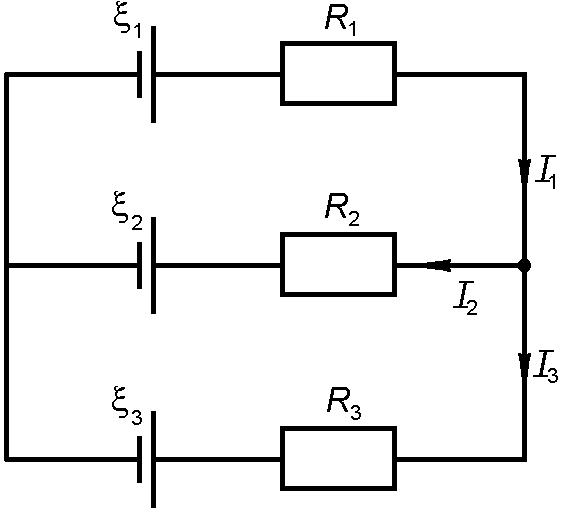
66. Найти силы тока во всех участках цепи (рис2.4.23), если  В,
В,  В,
В, 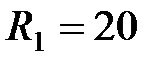 Ом,
Ом,  Ом. Внутренним сопротивлением источников пренебречь.
Ом. Внутренним сопротивлением источников пренебречь.

| 
|
Рис. 2.4.23 Рис. 2.4.24
67. Три источника с ЭДС  В,
В, 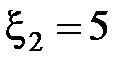 В,
В,  В и внутренними сопротивлениями
В и внутренними сопротивлениями 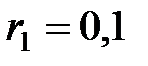 Ом,
Ом, 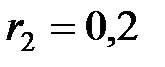 Ом,
Ом, 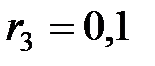 Ом соединены, как показано на рис. 2.4.24. Определить напряжения на резисторах сопротивлениями
Ом соединены, как показано на рис. 2.4.24. Определить напряжения на резисторах сопротивлениями 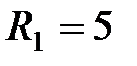 Ом,
Ом, 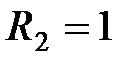 Ом,
Ом, 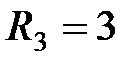 Ом.
Ом.
68. Найти силы тока во всех участках цепи (рис. 2.4.25), если 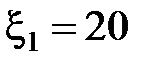 В,
В, 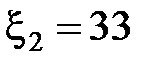 В,
В,  Ом,
Ом,  Ом,
Ом, 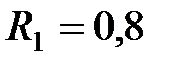 Ом,
Ом, 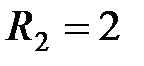 Ом.
Ом.
| 
|
Рис. 2.4.25 Рис. 2.4.26
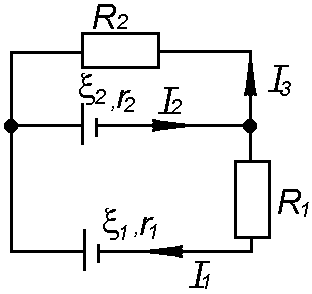
69. Два источника с ЭДС 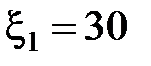 В,
В, 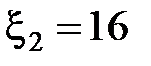 В и внутренними сопротивлениями
В и внутренними сопротивлениями 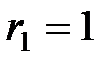 Ом,
Ом, 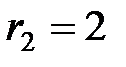 Ом включены параллельно (рис. 2.4.26) и работают на общую нагрузку сопротивлением
Ом включены параллельно (рис. 2.4.26) и работают на общую нагрузку сопротивлением  Ом. Определить силы тока во всех ветвях и мощность, потребляемую нагрузкой.
Ом. Определить силы тока во всех ветвях и мощность, потребляемую нагрузкой.
70. 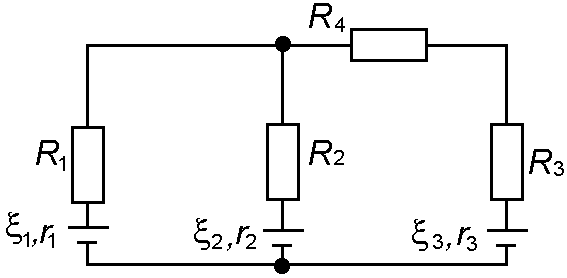 Рис. 2.4.27
Рис. 2.4.27
|
70 Как нужно соединить сопротивления 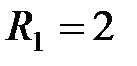 Ом,
Ом,  Ом, и
Ом, и 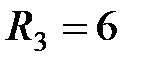 Ом, чтобы получить систему с
Ом, чтобы получить систему с  Ом?
Ом?
71 Определить силы тока во всех участках цепи (рис. 2.4.27) и мощность, развиваемую каждым источником тока, если 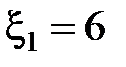 В,
В,  В,
В, 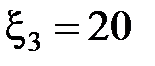 В,
В,  Ом,
Ом, 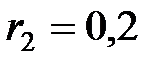 Ом,
Ом, 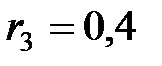 Ом,
Ом, 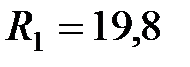 Ом,
Ом,  Ом,
Ом, 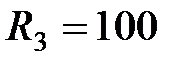 Ом,
Ом, 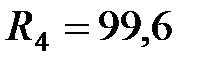 Ом.
Ом.
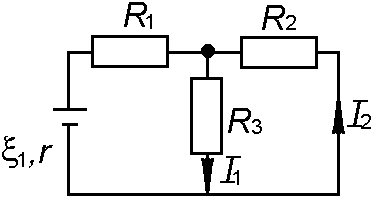
72 В схеме (рис. 2.4.28) 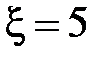 В,
В, 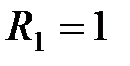 Ом,
Ом, 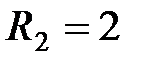 Ом,
Ом, 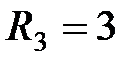 Ом. Сопротивление источника тока
Ом. Сопротивление источника тока  Ом. Найти силы токов
Ом. Найти силы токов 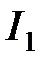 и
и 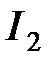 .
.
| 
|
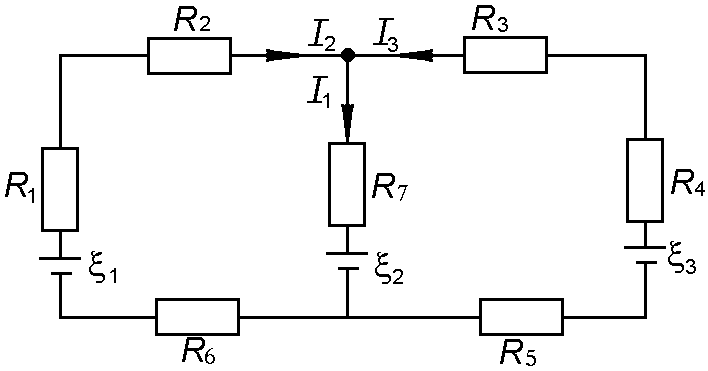
Рис. 2.4.28 Рис. 2.4.29
73. В схеме, изображенной на рис. 2.4.29, 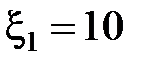 В,
В, 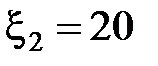 В,
В,  В,
В, 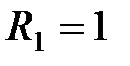 Ом,
Ом, 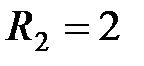 Ом,
Ом, 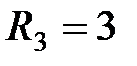 Ом,
Ом,  Ом,
Ом, 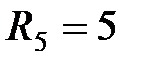 Ом,
Ом, 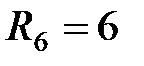 Ом,
Ом,  Ом. Внутреннее сопротивление источников мало. Найти силы токов
Ом. Внутреннее сопротивление источников мало. Найти силы токов 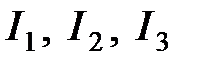 .
.
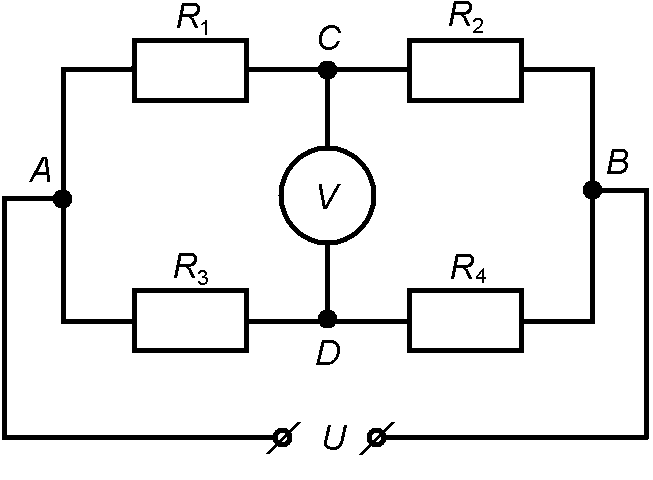
74. Какую разность потенциалов покажет вольтметр на рис. 2.4.30?
| 
|
Рис. 2.4.30 Рис. 2.4.31
75. Найти общее сопротивление участка цепи между точками А и В на рис. 2.4.31.
76. Зашунтированный амперметр измеряет токи силой до 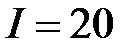 А. Какую наибольшую силу тока может измерить этот амперметр без шунта, если сопротивление амперметра
А. Какую наибольшую силу тока может измерить этот амперметр без шунта, если сопротивление амперметра  равно 0,02 Ом, а сопротивление шунта
равно 0,02 Ом, а сопротивление шунта 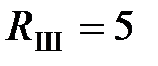 мОм?
мОм?
77. Найти температуру нити вольфрамовой лампы накаливания в рабочем состоянии, если известно, что сопротивление нити в момент включения при температуре 20° С в 12,6 раза меньше, чем в рабочем состоянии.
78. Из медной проволоки длиной 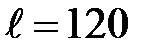 м и площадью поперечного сечения S = 24 мм2 намотана катушка. Найти приращение сопротивления катушки при ее нагревании от
м и площадью поперечного сечения S = 24 мм2 намотана катушка. Найти приращение сопротивления катушки при ее нагревании от 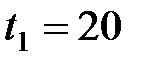 ° С до
° С до 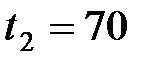 ° С.
° С.
79. Электрический чайник имеет две обмотки. При включении одной из них вода в чайнике закипает через 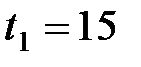 мин, при включении другой – через
мин, при включении другой – через 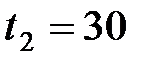 мин. Через какое время
мин. Через какое время 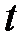 закипит вода в чайнике, если включить две обмотки: а) последовательно; б) параллельно?
закипит вода в чайнике, если включить две обмотки: а) последовательно; б) параллельно?
80. Электрический чайник вместимостью 1,5 дм3 имеет сопротивление нагревательного элемента 80 Ом, КПД 80 % и работает при напряжении 220 В. Начальная температура воды 20° С. Определить мощность тока, потребляемую чайником, силу тока в нагревательном элементе, время, в течение которого вода в чайнике закипит.
Магнитное поле
81. Два бесконечно длинных проводника скрещены под прямым углом. По проводникам текут токи силой I 1 = 100 А и I 2 = 50 А. Расстояние между проводниками d = 0,2 м. Определить индукцию магнитного поля в точке, лежащей на середине общего перпендикуляра к проводникам.
82. По двум бесконечно длинным параллельным проводникам текут токи одного направления величиной 15 А. Вычислить напряженность магнитного поля в точке, которая расположена на расстоянии 40 см от одного проводника и 30 см от другого, если расстояние между ними 50 см.
83. Плоский контур с током силой I = 5 А свободно установился в однородном магнитном поле с индукцией B = 0,4 Тл. Площадь контура S = 200 см2. Поддерживая ток в контуре неизменным, его повернули относительно оси, лежащей в плоскости контура, на угол α = 40º. Определить совершенную при этом работу.
84. В однородном магнитном поле перпендикулярно линиям индукции расположен плоский контур площадью S = 100 см2. Поддерживая в контуре постоянную силу тока I = 50 А, его переместили из поля в область пространства, где поле отсутствует. Определить индукцию B магнитного поля, если при перемещении контура была совершена работа A = 0,4 Дж.
85. Какова напряженность магнитного поля в центре квадрата со стороной a = 10 см, если по его периметру протекает ток силой I = 20 А?
86. Проводник согнут в виде правильного треугольника со стороной a = 20 см. Какой ток протекает по периметру треугольника, если в его центре напряженность поля H = 71,64 А/м?
87. Определить частоту n обращения электрона по круговой орбите в магнитном поле (B = 1 Тл).
88. Протон, получивший скорость в результате прохождения разности потенциалов U = 1 кВ, попадает в однородное магнитное поле с индукцией B = 0,2 Тл перпендикулярно линиям индукции. Определить радиус окружности, по которой будет двигаться протон, и период его вращения.
89. Заряженная частица прошла ускоряющую разность потенциалов и влетела в скрещенные под прямым углом электрическое (E = 400 В/м) и магнитное (B = 0,2 Тл) поля. Определить ускоряющую разность потенциалов U, если двигаясь перпендикулярно полям, частица не испытывает отклонений от прямолинейной траектории. Отношение заряда к массе частицы q / m = 9,64 ∙ 107 Кл/кг.
90. Плоский конденсатор, между пластинами которого создано электрическое поле (E = 100 В/м), помещен в магнитное поле так, что силовые линии полей взаимно перпендикулярны. Какова должна быть индукция B магнитного поля, чтобы электрон с начальной энергией E к = 4 кэВ, влетевший в пространство между пластинами конденсатора перпендикулярно силовым линиям магнитного поля, не изменил направления скорости?
91. Электрон движется по окружности радиусом R = 1 см в магнитном поле с индукцией B = 0,02 Тл. Какова кинетическая энергия электрона?
92. Заряженная частица с кинетической энергией E к = 2 кэВ движется в однородном магнитном поле по окружности радиусом R = 4 мм. Определить силу Лоренца, действующую на частицу со стороны поля.
93. Электрон, ускоренный разностью потенциалов U = 0,5 кВ, движется параллельно прямолинейному длинному проводнику на расстоянии 1 см от него. Определить силу, действующую на электрон, если по проводнику течет ток I = 10 А.
94. В однородном магнитном поле (B = 0,1 Тл) равномерно с частотой n = 5 с-1 вращается стержень длиной 50 см так, что плоскость его вращения перпендикулярна линиям напряженности, а ось вращения проходит через один из концов. Определить индуцируемую на концах стержня разность потенциалов U.
95. Железнодорожные рельсы изолированы друг от друга и от Земли и соединены через милливольтметр. Каково показание прибора, если по рельсам проходит поезд со скоростью 20 м/с? Вертикальную составляющую напряженности магнитного поля Земли принять равной 40 А/м, а расстояние между рельсами 1,54 м.
96. На цилиндрический железный сердечник длиной 0,1 м намотан провод длиной 10 м. Определить индуктивность полученного соленоида. Магнитная проницаемость железа μ = 400.
97. На 1 см однослойного соленоида без сердечника приходится 40 витков. Объем соленоида 800 см3. При какой скорости изменения силы тока в соленоиде индуцируется ЭДС самоиндукции 0,4 В?
98. В соленоиде сила тока равномерно возрастает от 0 до 50 А в течении 0,5 с, при этом соленоид накапливает энергию 50 Дж. Какая ЭДС индуцируется в соленоиде?
99. Магнитный поток Ф в соленоиде, содержащем N = 1000 витков, равен 0,2 мВб. Определить энергию W магнитного поля соленоида, если сила тока, протекающего по виткам соленоида, I = 1 А. Сердечник отсутствует. Магнитное поле во всем объеме соленоида считать однородным.
100. Определить энергию магнитного поля соленоида, содержащего N = 500 витков, которые намотаны на картонный каркас радиусом 2 см и длиной 0,5 м, если по нему идет ток I = 5 А.
101. Соленоид с сердечником из никеля на длине 0,5 м имеет N = 1000 витков с площадью поперечного сечения S = 50 см2. Определить магнитный поток внутри соленоида и энергию магнитного поля, если сила тока в соленоиде I = 10 А и магнитная проницаемость никеля μ = 200.
102. По проводнику, изогнутому в виде кольца радиусом R = 20 см, содержащему N = 500 витков, течет ток силой I = 1 А. Определить объемную плотность w энергии магнитного поля в центре кольца.
103. При какой силе тока I в прямолинейном проводе бесконечной длины на расстоянии r = 5 см от него объемная плотность энергии магнитного поля будет w = 1 мДж/м3?
104. Два бесконечно длинных прямолинейных проводника с токами 6 и 8 А расположены перпендикулярно друг другу. Определить индукцию и напряженность магнитного поля на середине кратчайшего расстояния между проводниками, равного 20 см.
105. По двум бесконечно длинным прямолинейным параллельным проводникам, расстояние между которыми 15 см, в одном направлении текут токи 4 и 6 А. Определить расстояние от проводника с меньшим током до геометрического места точек, в котором напряженность магнитного поля равна нулю.
106. Решить задачу 105 для случая, когда токи текут в противоположных направлениях.
107. Электрон движется в однородном магнитном поле, магнитная индукция которого 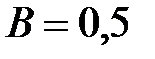 Тл. Вектор скорости электрона перпендикулярен вектору
Тл. Вектор скорости электрона перпендикулярен вектору 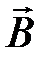 . Сколько оборотов сделает электрон за время
. Сколько оборотов сделает электрон за время 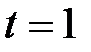 с?
с?
108. Квадратная проводящая рамка площадью 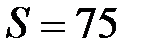 см2 за время
см2 за время 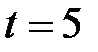 мс вносится в магнитное поле, индукция которого
мс вносится в магнитное поле, индукция которого  Тл перпендикулярна плоскости рамки. Сопротивление рамки
Тл перпендикулярна плоскости рамки. Сопротивление рамки  Ом. Определить среднюю силу индукционного тока, возникающего в рамке.
Ом. Определить среднюю силу индукционного тока, возникающего в рамке.
109. По цилиндрической катушке, имеющей  витков, течет ток
витков, течет ток 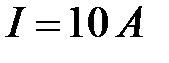 . При этом магнитный поток через один виток
. При этом магнитный поток через один виток 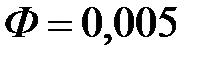 Bб. Определить энергию магнитного поля катушки.
Bб. Определить энергию магнитного поля катушки.
110. Электрон, ускоренный разностью потенциалов U = 6 кВ, влетает в однородное магнитное поле под углом 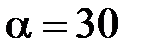 ° к направлению поля и начинает двигаться по винтовой линии. Индукция магнитного поля В = 1,3×10-2 Тл. Найти радиус витка и шаг винтовой линии.
° к направлению поля и начинает двигаться по винтовой линии. Индукция магнитного поля В = 1,3×10-2 Тл. Найти радиус витка и шаг винтовой линии.
111. Заряженная частица движется в магнитном поле по окружности со скоростью 106 м/с. Индукция магнитного поля 0,3 Тл. Радиус окружности 4 см. Найти заряд частицы, если известно, что ее энергия 12 кэВ.
112. Чему равна сила тока, проходящего по периметру правильного шестиугольника со стороной а = 20 см, если в его центре магнитная индукция В = 10 мкТл?
113. Проволочное кольцо радиусом 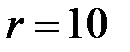 см лежит на столе. Какое количество электричества Q пройдет по кольцу, если его повернуть с одной стороны на другую? Сопротивление кольца R = 1 Ом. Вертикальная составляющая индукции В магнитного поля Земли равна 50 мкТл.
см лежит на столе. Какое количество электричества Q пройдет по кольцу, если его повернуть с одной стороны на другую? Сопротивление кольца R = 1 Ом. Вертикальная составляющая индукции В магнитного поля Земли равна 50 мкТл.
114. Индуктивность соленоида длиной 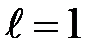 м, намотанного в один слой на немагнитный каркас, равна
м, намотанного в один слой на немагнитный каркас, равна  мГн. Площадь сечения соленоида S = 20 см2. Определить число витков п на каждом сантиметре длины соленоида.
мГн. Площадь сечения соленоида S = 20 см2. Определить число витков п на каждом сантиметре длины соленоида.
115. Катушка, намотанная на немагнитный цилиндрический каркас, имеет 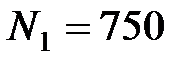 витков и индуктивность
витков и индуктивность 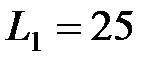 мГн. Чтобы увеличить индуктивность катушки до
мГн. Чтобы увеличить индуктивность катушки до 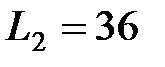 мГн, обмотку с катушки сняли и заменили обмоткой из более тонкой проволоки с таким расчетом, чтобы длина катушки осталась прежней. Определить число витков катушки после перемотки.
мГн, обмотку с катушки сняли и заменили обмоткой из более тонкой проволоки с таким расчетом, чтобы длина катушки осталась прежней. Определить число витков катушки после перемотки.
116. Виток, по которому течет ток I = 20 А, свободно установился в однородном магнитном поле с индукцией В = 0,016 Тл. Диаметр D витка равен 10 см. Определить работу А, которую нужно совершить, чтобы повернуть виток на угол: а)  относительно оси, совпадающей с диаметром; б)
относительно оси, совпадающей с диаметром; б)  .
.
117. Квадратная рамка со стороной а = 10 см, по которой течет ток 200 А, свободно устанавливается в однородном магнитном поле (В = 0,2 Тл). Определить работу, которую необходимо совершить при повороте рамки вокруг оси, лежащей в плоскости рамки и перпендикулярной линиям магнитной индукции, на угол  .
.
118. Прямой провод длиной 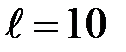 см, по которому течет ток
см, по которому течет ток 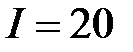 А, находится в однородном магнитном поле с индукцией В = 0,01 Тл. Найти угол
А, находится в однородном магнитном поле с индукцией В = 0,01 Тл. Найти угол 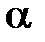 между направлением вектора
между направлением вектора 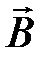 и током, если на провод действует сила
и током, если на провод действует сила  мН.
мН.
119. Квадратная проволочная рамка расположена в одной плоскости с длинным проводом так, что две ее стороны параллельны проводу. По рамке и проводу текут одинаковые токи  кА. Определить силу
кА. Определить силу 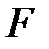 , действующую на рамку, если ближайшая к проводу сторона рамки находится на расстоянии, равном ее длине.
, действующую на рамку, если ближайшая к проводу сторона рамки находится на расстоянии, равном ее длине.
120. Определить индукцию В и напряженность Н магнитного поля на оси тороида без сердечника, по обмотке которого, содержащей 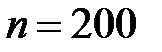 витков, идет ток
витков, идет ток  А. Внешний диаметр
А. Внешний диаметр 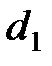 тороида равен 30 см, внутренний
тороида равен 30 см, внутренний  см.
см.
КОЛЕБАНИЯ И ВОЛНЫ
Механические колебания
1. Найти зависимость ускорения гармонического колебания 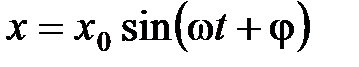 от смещения. Построить график зависимости ускорения от смещения.
от смещения. Построить график зависимости ускорения от смещения.
2. К упругой пружине подвешивают груз, в результате чего пружина растягивается на 2 см. Напишите уравнение гармонических колебаний, складывающихся при условии, что пружина дополнительно растягивается на 2 см и освобождается.
3. Начальная фаза гармонического колебания материальной точки равна нулю. Через какую долю периода скорость точки будет равна половине ее максимальной скорости?
4. Амплитуда гармонического колебания 10 см, период 0,5 с. Написать уравнение гармонических колебаний. Определить максимальную скорость и максимальное ускорение.
5. Математический маятник с длиной нити 5 м и массой подвешенного тела 0,1 кг в начальный момент времени находится в положении равновесия. Маятнику сообщается в горизонтальном направлении начальная скорость  . Написать уравнение последующих колебаний маятника.
. Написать уравнение последующих колебаний маятника.
6. Однородный стержень длиной 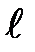 колеблется около оси, проходящей через его верхний конец. Найти циклическую частоту и период колебаний. Сделать расчёты для
колеблется около оси, проходящей через его верхний конец. Найти циклическую частоту и период колебаний. Сделать расчёты для 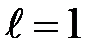 м.
м.
7. Обруч, подвешенный на гвозде, совершает малые колебания. Определить период и частоту колебаний обруча, если известно, что радиус обруча 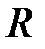 .
.
8. Однородный картонный диск радиусом 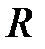 совершает колебания около горизонтально вбитого гвоздя. На каком расстоянии от центра следует пробить отверстие, чтобы период колебаний был минимальным?
совершает колебания около горизонтально вбитого гвоздя. На каком расстоянии от центра следует пробить отверстие, чтобы период колебаний был минимальным?
9. Льдина толщиной 10 см и площадью  см2 плавает на поверхности пруда. С какой частотой она будет колебаться, если её несколько погрузить в воду, а затем отпустить?
см2 плавает на поверхности пруда. С какой частотой она будет колебаться, если её несколько погрузить в воду, а затем отпустить?
10. Тело массой  совершает колебания по закону
совершает колебания по закону 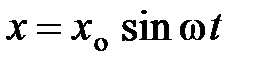 . Найти его максимальную кинетическую энергию и закон изменения силы, действующей на тело в процессе колебаний.
. Найти его максимальную кинетическую энергию и закон изменения силы, действующей на тело в процессе колебаний.
11. Начальная фаза гармонического колебания материальной точки равна нулю. При смещении точки от положения равновесия на 2,4 см её скорость 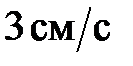 , а при смещении равном 2,8 скорость равна
, а при смещении равном 2,8 скорость равна  . Найти амплитуду и период колебаний.
. Найти амплитуду и период колебаний.
12. Найти логарифмический декремент затухания, если у математического маятника длиной 1 м амплитуда колебаний уменьшилась за 1 мин в 2 раза.
13. Амплитуда затухающих колебаний за 1 мин уменьшается в 2 раза. Во сколько раз она уменьшится за 3 минуты?
14. Начальная амплитуда колебаний математического маятника А 1 = 20 см, амплитуда после 10 полных колебаний равна А 10 = 1 см. Определить логарифмический декремент затухания и коэффициент затухания, если период колебаний Т = 5 с. Записать уравнение колебания.
15. К невесомой пружине подвесили грузик, и она растянулась на D х = 9,8 см. С каким периодом будет колебаться грузик, если дать ему небольшой толчок в вертикальном направлении? Логарифмический декремент затухания Q= 3,1.
16. Найти добротность осциллятора, у которого амплитуда смещения уменьшается в h = 2,0 раза через каждые n =110 периодов колебаний.
17. Найти добротность осциллятора, у которого собственная частота w0 = 10 c–1 и время релаксации t= 60 с.
18. Во сколько раз изменится период вертикальных колебаний груза, подвешенного к двум последовательно соединённым одинаковым пружинам, если пружины соединить параллельно?
19. Определить период колебаний ртути, находящейся в U – образной трубке. Площадь сечения трубки S =0,3 см2, масса ртути m = 121 г.
20. Точка одновременно участвует в двух взаимно перпендикулярных колебаниях, уравнения которых 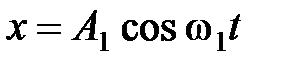 ,
,  , где
, где 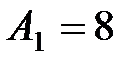 см,
см, 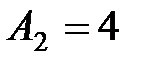 см,
см, 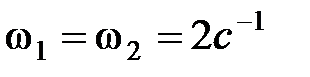 . Написать уравнение траектории, построить её на чертеже, показать начальное состояние и направление движения.
. Написать уравнение траектории, построить её на чертеже, показать начальное состояние и направление движения.
21. Определить максимальное ускорение материальной точки, совершающей гармонические колебания с амплитудой  см, если наибольшая скорость точки
см, если наибольшая скорость точки  .Написать уравнение колебаний.
.Написать уравнение колебаний.
22. Амплитуда гармонических колебаний материальной точки 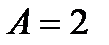 см, полная энергия
см, полная энергия 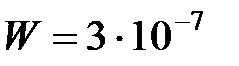 Дж. При каком смещении от положения равновесия на колеблющуюся точку действует сила
Дж. При каком смещении от положения равновесия на колеблющуюся точку действует сила 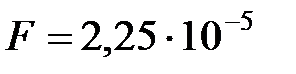 H?
H?
23. Маленький шарик, подвешенный на нити длиной 20 см, отклоняют на угол 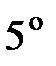 и наблюдают его колебания. Найти скорость шарика при прохождении им положения равновесия (двумя способами).
и наблюдают его колебания. Найти скорость шарика при прохождении им положения равновесия (двумя способами).
24. При какой скорости поезда маятник длиной 1 м, подвешенный в вагоне, особенно сильно раскачается, если длина рельс между стыками 12,5 м?
25. В поезде, движущемся равномерно, период колебаний математического маятника 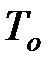 . Каким будет период колебаний, если поезд начнёт тормозить с ускорением, равным
. Каким будет период колебаний, если поезд начнёт тормозить с ускорением, равным 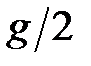 ?
?
26. На каком расстоянии от центра нужно подвесить тонкий стержень длиной 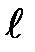 , чтобы получить физический маятник, колеблющийся с максимальной частотой? Чему равна эта частота?
, чтобы получить физический маятник, колеблющийся с максимальной частотой? Чему равна эта частота?
27. Найти закон, по которому изменяется натяжение нити математического маятника, совершающего колебания 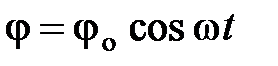 . Масса маятника
. Масса маятника 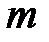 .
.
28. Написать уравнение гармонического колебания, если максимальное ускорение точки  , период колебаний 2с и смещение точки от положения равновесия в начальный момент времени 2,5 см.
, период колебаний 2с и смещение точки от положения равновесия в начальный момент времени 2,5 см.
29. Материальная точка массой 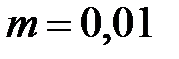 кг движется по закону
кг движется по закону 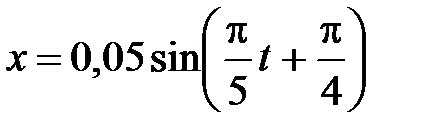 м. Найти максимальную силу, действующую на точку и полную энергию колебания.
м. Найти максимальную силу, действующую на точку и полную энергию колебания.
30. Пружинный маятник массой 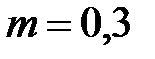 кг совершает колебания с амплитудой
кг совершает колебания с амплитудой 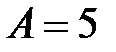 см. Зная, что полная энергия колебаний равна 1 Дж, найти коэффициент упругости пружины и период колебаний.
см. Зная, что полная энергия колебаний равна 1 Дж, найти коэффициент упругости пружины и период колебаний.
31. Медный шарик, подвешенный к пружине, совершает колебания с периодом 1 с. Как и на сколько изменится период колебаний, если медный шарик заменить алюминиевым такого же размера? Плотность меди 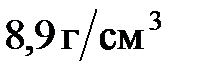 , плотность алюминия
, плотность алюминия 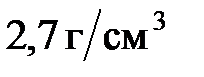 .
.
32. Частота колебаний стального шарика радиусом 1 см, прикрепленного к пружине, в воздухе ω0 = 5 с-1, а в жидкости ω = 4 с-1. Определить вязкость жидкости.
33. Тело движется под действием силы 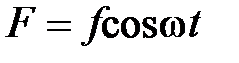 по закону
по закону 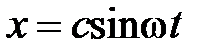 . Найти работу за время, прошедшее от момента t 1 до момента t 2. Найти работу силы за один период и среднюю мощность за период.
. Найти работу за время, прошедшее от момента t 1 до момента t 2. Найти работу силы за один период и среднюю мощность за период.
34. На тело действует сила 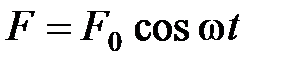 . Найти закон движения тела при начальных условиях при t = 0, x = 0,
. Найти закон движения тела при начальных условиях при t = 0, x = 0, 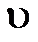 = 0. Определить период колебания, наибольшее значение x (t) и наибольшее значение скорости. Масса движущейся частицы m.
= 0. Определить период колебания, наибольшее значение x (t) и наибольшее значение скорости. Масса движущейся частицы m.
35. Определить отношение потенциальной энергии гармонически колеблющейся точки к ее кинетической энергии, если известна фаза колебаний.
36. Материальная точка участвует в двух взаимно перпендикулярных колебаниях 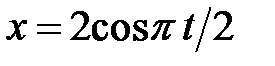 и
и 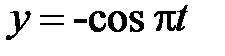 . Найдите уравнение траектории.
. Найдите уравнение траектории.
37. При сложении двух одинаково направленных гармонических колебаний с одной и той же частотой и амплитудами, равными 2 см и 4 см, получается гармоническое колебание с амплитудой 5 см. Найти разность фаз складываемых колебаний.
38. Точка участвует одновременно в двух колебаниях одного направления, которые происходят по законам 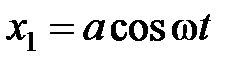 и
и 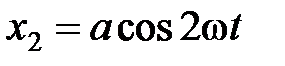 . Найти максимальную скорость точки.
. Найти максимальную скорость точки.
39. Найти уравнение траектории 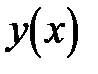 точки, если она движется по закону
точки, если она движется по закону 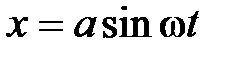 ,
,  .
.
40. Найти уравнение траектории 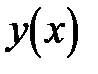 точки, если она движется по закону
точки, если она движется по закону 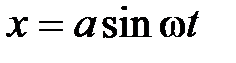 ,
, 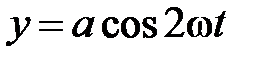 .
.




